Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T04:27:22.553Z Has data issue: false hasContentIssue false
  • English
  • Français

An analogue of Van der Corput's A5-process for exponential sums

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  26 February 2010

O. Robert
O. Robert
Affiliation:
Institut Elie Cartan, Université Henri Poincaré—Nancy I, BP 239, 54 506 Vandoeuvre-lès-Nancy Cedex, France. E-mail: [email protected]
Get access

Abstract

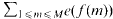A diophantine system is studied from which is deduced an analogue of van der Corput's A5-process in order to bound analytic exponential sums of the form . The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].

MSC classification

Secondary: 11L07: Estimates on exponential sums
Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 167 - 183
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Graham, S. W. and Kolesnik, G.. Van der Corput's Method for Exponential Sums. London Math. Soc. Lecture Notes Series 126 (Cambridge University Press, 1991).CrossRefGoogle Scholar
2.Hua, L. K.. On a theorem due to Vinogradov. Quarterly Journal of Maths, Oxford Series II, (1940), 161–176. (This paper is included in Loo-Keng Hua Selected Papers, edited by Halberstam, H.. Springer Verlag (1983).)Google Scholar
3.Robert, O.. Quelqucs paires d'exposants par la methode de Vinogradov. J. Théor. Nombres Bordeaux 14 (2002). 271–285.Google Scholar
4.Robert, O. and Sargos, P.. Un théorème de moyenne pour les sommes d'exponentielles. Applications a l'inégalité de Weyl. Publications Institute of the of Mathematics (Belgrade), 67 (81) (2000), 14–30.Google Scholar
5.Robert, O. and Sargos, P.. A fourth derivative test for exponential sums. Compositio Math., 130 (2002). 275–292.CrossRefGoogle Scholar
6.Sargos, P.. Points cntiers au voisinage d'une courbe, sommes trigonometriques courtes et paires d'exposants. Proc. London. Math. Soc., (3) 70 (1995), 285–312.CrossRefGoogle Scholar
7.Sareos, P.. Un critére de la dérivée cinquième pour les sommes d'exponentielles. Bull. London. Math. Soc., 32 (2000), 398–402.Google Scholar
8.Sargos, P.. An analog of van der Corput's A 4-process for exponential sums Acta Arith. 110 (2003), 219–231.CrossRefGoogle Scholar