Published online by Cambridge University Press: 22 May 2015
For some text algorithms, the real measure for the complexity analysis is not the string itself but its structure stored in its prefix table or equivalently border table. In this paper, we define the combinatorial class of prefix lists, namely a sequence of integers together with their size, and an injection ψ from the class of prefix tables to the class of prefix lists. We call a valid prefix list the image by ψ of a prefix table. In particular, we describe algorithms converting a prefix/border table to a prefix list and inverse linear algorithms from computing from a prefix list L = ψ(P) two words respectively in a minimal size alphabet and on a maximal size alphabet with P as prefix table. We then give a new upper bound on the number of prefix tables for strings of length n (on any alphabet) which is of order (1 + ϕ)n (with 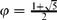 $\varphi=\frac{1+\sqrt{5}}{2}$ the golden mean) and also present a corresponding lower bound.
$\varphi=\frac{1+\sqrt{5}}{2}$ the golden mean) and also present a corresponding lower bound.