Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T00:56:58.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Some strong limit-2 and Dirichiet criteria for fourth order differential expressions

Published online by Cambridge University Press:  24 October 2008

David Race
David Race
Affiliation:
Mathematics Department, University of Surrey, Guildford, Surrey GU2 5XH
Get access Rights & Permissions [Opens in a new window]

Abstract

Conditions are given on the real coefficients p, q and r and the weight w, for the fourth order formally symmetric differential expression

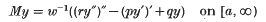
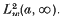to have the properties of being strong limit-2 and Dirichlet at ∞, when considered in the weighted Hilbert space, . These extend existing results due to both W. N. Everitt and V. Krishna Kumar and cover an expression which is important in the study of certain orthogonal polynomials.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 2 , September 1990 , pp. 409 - 416
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Everitt, V. N.. Some positive definite differential operators. J. London Math. Soc. 43 (1968), 465–473.CrossRefGoogle Scholar
[2]Everitt, W. N., Krall, A. M. and Littlejohn, L. L.. Some properties of the Laguerre(2) differential equation and associated orthogonal polynomials. (In preparation.)Google Scholar
[3]Frentzen, H.. Limit-point criteria for symmetric, J-symmetric and arbitrary quasi-differential expressions. Proc. London Math. Soc. 51 (1985), 543–562.CrossRefGoogle Scholar
[4]Hinton, D.. Strong limit-point and Dirichlet criteria for ordinary differential expressions of order 2n. Proc. Roy. Soc. Edinburgh Ser. A 76 (1977), 301–310.CrossRefGoogle Scholar
[5]Kumar, V. Krishna. The strong limit-2 case of fourth-order differential equations. Proc. Roy. Soc. Edinburgh Ser. A 71 (1974), 297–304.Google Scholar
[6]Kumar, V. Krishna. On the strong limit-point classification of fourth-order differential expressions with complex coefficients. J. London Math. Soc. 12 (1976), 287–298.CrossRefGoogle Scholar