Published online by Cambridge University Press: 24 October 2008
Let f be an entire function of the form
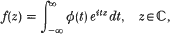
where ø is a function in L2(ℝ) with compact support. If f|ℝ is real-valued then, for obvious reasons, (a) the supporting interval for ø is symmetric with respect to the origin, and

Assuming that f has no zeros in {Im z > 0}, we prove that the converse is also true: (a) and (b) together imply that f|ℝ takes values in αℝ, where α is a fixed complex number.
The proof relies on a certain formula involving the Dirichlet integral, which may be interesting on its own.