No CrossRef data available.
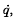 , p space
, p spacePublished online by Cambridge University Press: 24 October 2008
An alternative definition is proposed for the kernel used by Feynman. This definition involves a functional integration in a q, 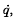 , p space, treating these variables as independent. The equivalence of this definition to the Feynman one and to the one using the variables q, p is exhibited.
, p space, treating these variables as independent. The equivalence of this definition to the Feynman one and to the one using the variables q, p is exhibited.