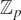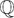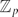Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ITOH, Tsuyoshi
and
TAKAKURA, Yu
2014.
On Tamely Ramified Iwasawa Modules for $\Zp$-extensions of Imaginary Quadratic Fields.
Tokyo Journal of Mathematics,
Vol. 37,
Issue. 2,
Mizusawa, Yasushi
2017.
Tame pro-2 Galois groups and the basic ℤ₂-extension.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 4,
p.
2423.
Mizusawa, Yasushi
2019.
On pro-𝑝 link groups of number fields.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 10,
p.
7225.
ITOH, Tsuyoshi
2020.
On the Structure of the Galois Group of the Maximal Pro-$p$ Extension with Restricted Ramification over the Cyclotomic $\mathbb{Z}_p$-extension.
Tokyo Journal of Mathematics,
Vol. 43,
Issue. 1,