Published online by Cambridge University Press: 24 October 2008
In Chapter v of his Les Méthodes Nouvelles de la Mécanique Céleste Poincaré proves a theorem which he calls The non-existence of Uniform Integrals. This theorem is as follows:
Let
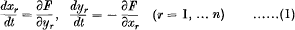
be a system of equations in which the characteristic function F is expanded in a series
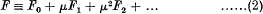
convergent for sufficiently small values of | μ |, for all real values of y1, … yn, and for values of x1, … xn within certain finite real intervals; while F0, F1; … are analytic functions of x1, … xn, y1, … yn, of which F0 is independent of y1, … yn and Fl, F2, … are periodic with respect to these variables with period 2π.
* These intervals are of course to be such that within them the derivatives of F are finite and continuous.
* This statement requires some justification. If P be any point (at which the derivatives of F 0 are finite and continuous) of a space for which x 1, … x n are Cartesian coordinates, we may determine a locus, L 0 say, of the family (10), in which we regard m 1, … m n as continuously variable parameters, to pass through P. Allowing m 1, … m n to vary continuously from their values for L 0, the locus represented by (10) will undergo a continuous displacement in the neighbourhood of P. In any such variation, however small, m 1, … m n simultaneously pass through rational values; thus, since m 1, … m n enter (10) only through their ratios, we can find a locus of the family for which m 1, … m n have integral values, to pass arbitrarily near P.
* Méthodes Nouvelles, § 87.
‡ Acta Math., xxx (1905), 305.Google Scholar
‡ Analytical Dynamics (2nd ed.), p. 385.Google Scholar
§ Phys. Zeit., xxiv (1923), 261Google Scholar.
∥ See, for example, Born, and Pauli, , Zeit. für Phys., x, 137, § 3.Google Scholar
* ‘Integrals of Systems of Ordinary Differential Equations,” p. 273, above.
* If the equations be taken in Poincaré's form (1), the special property of the value μ = 0 is that then the equations simplify in such a far-reaching manner that their solution becomes trivial; we thus reach the paradoxical conclusion that expansions in powers of μ are unsuitable for the precise reason which originally led to their adoption! In fact, as has been remarked by Poincaré, we get into unnecessary difficulties by taking too simple a first approximation; it is this same idea which underlies Gylden's contributions to Celestial Mechanics.
† See p. 281, above.