No CrossRef data available.
Bisecant curves of ruled surfaces
Published online by Cambridge University Press: 24 October 2008
Extract
The bisecant curves of a ruled surface, that is to say the curves on the surface which meet each generator in two points, are fundamental in the consideration of the normal space of the ruled surface. It is well known that if 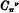 is a bisecant curve of order ν and genus π on a ruled surface of order N and genus P, then
is a bisecant curve of order ν and genus π on a ruled surface of order N and genus P, then
provided that the curve  has no double points which count twice as intersections of a generator of the ruled surface.
has no double points which count twice as intersections of a generator of the ruled surface.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 3 , 30 July 1933 , pp. 382 - 388
- Copyright
- Copyright © Cambridge Philosophical Society 1933
References
* Segre, , Math. Ann. 34 (1889), 2.CrossRefGoogle Scholar
† I hope to publish a paper on special ruled surfaces in the near future.
* Segre, , Math. Ann. 30 (1887), 222–223.Google Scholar
† In one of the papers referred to above Segre gives the impression that q is zero provided that the expression in brackets is not negative, but this is not true even with his supposition that n > 2p − 2; cf. Segre, , Math. Ann. 30 (1887), 222.Google Scholar
* The 2P points in which ![]() is met by C 1 and C 2 might offer less than 2P conditions, so that the number of further conditions to contain
is met by C 1 and C 2 might offer less than 2P conditions, so that the number of further conditions to contain ![]() would be greater. But the conditions for a quadric to contain C 1 and C 2 would be less by the same amount, and the total number of conditions would be unaltered.
would be greater. But the conditions for a quadric to contain C 1 and C 2 would be less by the same amount, and the total number of conditions would be unaltered.
* Segre, , Math. Ann. 34 (1889), 7.CrossRefGoogle Scholar
* The only surface with two double lines is the R 41 in [3].
† If the curve is special the ruled surface given by the γ12 is a cone.
* See § 8.


