Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-02T23:49:58.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Some remarks about a formula of Charles Dodgson

Published online by Cambridge University Press:  23 January 2015

Juan Pla
Juan Pla*
Affiliation:
315 rue de Belleville, 75019 Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

In this note we start by exploring a type of solution of the equation in positive integers

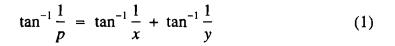
for a given p, which will enable us easily to derive a class of solutions in integers of the more general equation in positive integers

for any positive integers p and n.

In another part of this note we explore some connections between the formula we find and a particular chapter in the elementary theory of numbers.

Type
Articles
Information
The Mathematical Gazette , Volume 95 , Issue 533 , July 2011 , pp. 235 - 239
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abeles, Francine F., Charles L. Dodgson's geometric approach to arctangent relations for pi, Historia Mathematica 20 (1993) pp. 151–159.CrossRefGoogle Scholar
2. Wetherfield, Michael, The enhancement of Machin's formula by Todd's process, Math. Gaz. 80 (July 1996) pp. 333–344.CrossRefGoogle Scholar
3. Wrench, J. W., The evolution of extended decimal approximation to π, The Mathematics Teacher, 53 (December 1960) pp. 644–650.Google Scholar
4. Berggren, Lennart, Borwein, Jonathan and Borwein, Peter, Pi: A Source Book, Springer Verlag (1997).CrossRefGoogle Scholar
5. Wetherfield, Michael and Chien-Lih, Hwang, Some new inverse cotangent identities for π, Math. Gaz. 81 (November 1997) pp. 459–460.Google Scholar
6. Davenport, H., The higher arithmetic (5th edn.), Cambridge University Press (1982).Google Scholar
7. Frink, Orrin, Almost Pythagorean triples, Mathematics Magazine 60 (October 1987) pp. 234–236.CrossRefGoogle Scholar
8. Ore, Oystein, Number theory and its history, Dover Publications, Inc. New York (1988).Google Scholar
9. Bradley, C. J., On solutions of m2 + n2 = 1 + t2 , Math. Gaz. 80 (November 1996) pp. 404–406.CrossRefGoogle Scholar
10. Bradley, C. J., From integer Lorentz transformation to Pythagoras, Math. Gaz. 88 (March 2004) pp. 16–21.CrossRefGoogle Scholar
11. Dickson, Leonard E., Lowest integers representing sides of a right triangle, Am. Math. Monthly 1 (1894) pp. 6–11.CrossRefGoogle Scholar