Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-09T00:31:26.289Z Has data issue: false hasContentIssue false
  • English
  • Français

OBSERVABILITY OF BAOUENDI–GRUSHIN-TYPE EQUATIONS THROUGH RESOLVENT ESTIMATES

Part of: Elliptic equations and systems General mathematical topics and methods in quantum theory Controllability, observability, and system structure Spectral theory and eigenvalue problems Close-to-elliptic equations and systems

Published online by Cambridge University Press:  14 June 2021

Cyril Letrouit Open the ORCID record for Cyril Letrouit [Opens in a new window]  and
Chenmin Sun
Cyril Letrouit
Affiliation:
Sorbonne Université, Université Paris-Diderot SPC, CNRS, Inria, Laboratoire Jacques-Louis Lions, équipe CAGE, Paris F-75005, France DMA, École normale supérieure, CNRS, PSL Research University, Paris 75005, France ([email protected])
Chenmin Sun
Affiliation:
CY Cergy Paris Université, Laboratoire de Mathématiques AGM, UMR 8088 du CNRS, 2 av. Adolphe Chauvin, Cergy-Pontoise Cedex 95302, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study the observability (or equivalently, the controllability) of some subelliptic evolution equations depending on their step. This sheds light on the speed of propagation of these equations, notably in the ‘degenerated directions’ of the subelliptic structure.

First, for any 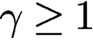$\gamma \geq 1$ , we establish a resolvent estimate for the Baouendi–Grushin-type operator 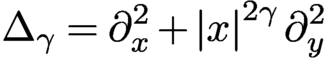$\Delta _{\gamma }=\partial _x^2+\left \lvert x\right \rvert ^{2\gamma }\partial _y^2$ , which has step 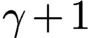$\gamma +1$ . We then derive consequences for the observability of the Schrödinger-type equation 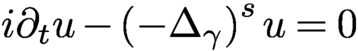$i\partial _tu-\left (-\Delta _{\gamma }\right )^{s}u=0$ , where 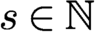$s\in \mathbb N$ . We identify three different cases: depending on the value of the ratio 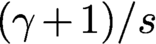$(\gamma +1)/s$ , observability may hold in arbitrarily small time or only for sufficiently large times or may even fail for any time.

As a corollary of our resolvent estimate, we also obtain observability for heat-type equations 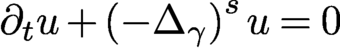$\partial _tu+\left (-\Delta _{\gamma }\right )^su=0$ and establish a decay rate for the damped wave equation associated with 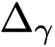$\Delta _{\gamma }$ .

Keywords

observabilitysubelliptic equationsSchrödinger equationresolvent estimates

MSC classification

Primary: 93B07: Observability 35H20: Subelliptic equations 35J10: Schrödinger operator
Secondary: 35P10: Completeness of eigenfunctions, eigenfunction expansions 81Q20: Semiclassical techniques, including WKB and Maslov methods
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 2 , March 2023 , pp. 541 - 579
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman, N. and Léautaud, M., Sharp polynomial decay rates for the damped wave equation on the torus, Anal. PDE 7 (2014), 159–214.CrossRefGoogle Scholar
Anantharaman, N. and Macià, F., Semiclassical measures for the Schrödinger equations on the torus, J. Eur. Math. Soc. (JEMS) 16(6) (2014), 1253–1288.CrossRefGoogle Scholar
Bahouri, H., Gérard, P. and Xu, C.-J., Espaces de Besov et estimations de Strichartz généralisées sur le groupe de Heisenberg, J. Anal. Math. 82 (2000), 93–118.CrossRefGoogle Scholar
Bardos, C., Lebeau, G. and Rauch, J., Sharp sufficient conditions for the observation, control, and stabilization of waves from the boundary, SIAM J. Control Optim. 30(5) (1992), 1024–1065.CrossRefGoogle Scholar
Beauchard, K., Cannarsa, P. and Guglielmi, R., Null controllability of Grushin-type operators in dimension two, J. Eur. Math. Soc. (JEMS) 16(1) (2014), 67–101.CrossRefGoogle Scholar
Borichev, A. and Tomilov, Y., Optimal polynomial decay of functions and operator semigroups, Math. Ann. 347(2) (2010), 455–478.CrossRefGoogle Scholar
Burq, N., Gérard, P. and Tzvetkov, N., Strichartz inequalities and the nonlinear Schrödinger equation on compact manifolds, Amer. J. Math. 126(3) (2004), 569–605.CrossRefGoogle Scholar
Burq, N. and Sun, C., Time optimal observability for the Grushin-Schrödinger equation, Anal. PDE, to appear.Google Scholar
Burq, N. and Zworski, M., Geometric control in the presence of a black box, J. Amer. Math. Soc. 17(2) (2004), 443–471.CrossRefGoogle Scholar
Burq, N. and Zworski, M., Control for Schrödinger operators on tori, Math. Res. Lett. 19(2) (2012), 309–324.CrossRefGoogle Scholar
Colin de Verdière, Y., Hillairet, L. and Trélat, E., Spectral asymptotics for sub-Riemannian Laplacians, I: Quantum ergodicity and quantum limits in the 3-dimensional contact case, Duke Math. J. 167(1) (2018), 109–174.CrossRefGoogle Scholar
Dimassi, M. and Sjostrand, J., Spectral asymptotics in the semi-classical limit, London Mathematical Society Lecture Note Series. No 268. Cambridge University Press, 1999.CrossRefGoogle Scholar
Duyckaerts, T. and Miller, L., Resolvent conditions for the control of parabolic equations, J. Funct. Anal. 263(11) (2012), 3641–3673.CrossRefGoogle Scholar
Fermanian Kammerer, C. and Letrouit, C., Observability and controllability for the Schrödinger equation on quotients of groups of Heisenberg type, Preprint, 2020, arXiv:2009.13877.CrossRefGoogle Scholar
Garofalo, N., Unique continuation for a class of elliptic operators which degenerate on a manifold of arbitrary codimension, J. Differential Equations 104(1) (1993), 117–146.CrossRefGoogle Scholar
Hörmander, L., On the existence and the regularity of solutions of linear pseudodifferential equations, Enseign. Math. 17(2) (1971), 99–163. Google Scholar
Koenig, A., Non-null-controllability of the Grushin operator in 2D, C. R. Math. Acad. Sci. Paris 355(12) (2017), 1215–1235.CrossRefGoogle Scholar
Laurent, C. and Léautaud, M., Logarithmic decay for damped hypoelliptic wave and Schrödinger equations, to appear in SIAM J. Cont. Opt., 2020, arXiv:2006.05122.CrossRefGoogle Scholar
Lebeau, G., Contrôle de l’équation de Schrödinger, J. Math. Pures Appl. (9) 71(3) (1992), 267–291.Google Scholar
Letrouit, C., Subelliptic wave equations are never observable, Preprint, 2020, arXiv:2002.01259.Google Scholar
Lions, J.-L., Contrôlabilité exacte, perturbations et stabilisation de systèmes distribués. Tome 1. Rech . Math. Appl. 8 (Masson, Paris, 1988).Google Scholar
Lions, J. L. and Peetre, J., Sur une classe d’espaces d’interpolation, Publ. Math. Inst. Hautes Études Sci. 19 (1964), 5–68.CrossRefGoogle Scholar
Miller, L., Resolvent conditions for the control of unitary groups and their approximations, J. Spectr. Theory 2(1) (2012), 1–55.CrossRefGoogle Scholar
Rivas, I. and Sun, C.-M., Internal controllability for the Kadomtsev-Petviashvili II equation, SIAM J. Control Optim. 58(3) (2020), 1715–1734.CrossRefGoogle Scholar
Simon, B., Coupling constant analyticity for the anharmonic oscillator, Ann. Physics 58 (1970), 76–136.CrossRefGoogle Scholar
Taylor, M. E., Partial Differential Equations I, Applied Mathematical Sciences, 115 (Springer Verlag, New York, 2011).CrossRefGoogle Scholar