Published online by Cambridge University Press: 21 March 2022
This work is devoted to the study of uncertainty principles for finite combinations of Hermite functions. We establish some spectral inequalities for control subsets that are thick with respect to some unbounded densities growing almost linearly at infinity, and provide quantitative estimates, with respect to the energy level of the Hermite functions seen as eigenfunctions of the harmonic oscillator, for the constants appearing in these spectral estimates. These spectral inequalities allow us to derive the null-controllability in any positive time for evolution equations enjoying specific regularizing effects. More precisely, for a given index 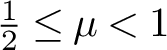 $\frac {1}{2} \leq \mu <1$, we deduce sufficient geometric conditions on control subsets to ensure the null-controllability of evolution equations enjoying regularizing effects in the symmetric Gelfand–Shilov space
$\frac {1}{2} \leq \mu <1$, we deduce sufficient geometric conditions on control subsets to ensure the null-controllability of evolution equations enjoying regularizing effects in the symmetric Gelfand–Shilov space 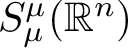 $S^{\mu }_{\mu }(\mathbb {R}^{n})$. These results apply in particular to derive the null-controllability in any positive time for evolution equations associated to certain classes of hypoelliptic non-self-adjoint quadratic operators, or to fractional harmonic oscillators.
$S^{\mu }_{\mu }(\mathbb {R}^{n})$. These results apply in particular to derive the null-controllability in any positive time for evolution equations associated to certain classes of hypoelliptic non-self-adjoint quadratic operators, or to fractional harmonic oscillators.