Published online by Cambridge University Press: 27 May 2020
Under an assumption on the existence of 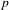 $p$-adic Galois representations, we carry out Taylor–Wiles patching (in the derived category) for the completed homology of the locally symmetric spaces associated with
$p$-adic Galois representations, we carry out Taylor–Wiles patching (in the derived category) for the completed homology of the locally symmetric spaces associated with 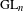 $\operatorname{GL}_{n}$ over a number field. We use our construction, and some new results in non-commutative algebra, to show that standard conjectures on completed homology imply ‘big
$\operatorname{GL}_{n}$ over a number field. We use our construction, and some new results in non-commutative algebra, to show that standard conjectures on completed homology imply ‘big 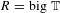 $R=\text{big}~\mathbb{T}$’ theorems in situations where one cannot hope to appeal to the Zariski density of classical points (in contrast to all previous results of this kind). In the case where
$R=\text{big}~\mathbb{T}$’ theorems in situations where one cannot hope to appeal to the Zariski density of classical points (in contrast to all previous results of this kind). In the case where 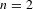 $n=2$ and
$n=2$ and 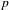 $p$ splits completely in the number field, we relate our construction to the
$p$ splits completely in the number field, we relate our construction to the 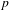 $p$-adic local Langlands correspondence for
$p$-adic local Langlands correspondence for 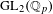 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$.
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$.
The first author was supported in part by a Leverhulme Prize, EPSRC grant EP/L025485/1, Marie Curie Career Integration Grant 303605, and by ERC Starting Grant 306326. The second author was supported by ERC Starting Grant 306326.