1 Introduction
In 2017, Google implemented “Project Sunroof”, an online tool that helps people installing solar panels and informs about the location of other users who are about to install or have already installed one. Apparently, “one of the best predictors of whether people install solar panels on their house isn’t their age, race, income, or political affiliation. It’s whether their neighbors did it first.”Footnote 1
Examples of behaviors whose decisive momentum is influenced by social intentions are ubiquitous, e.g., social movements often result from awareness of similar intentions to fight for democracy, peace, against pollution, etc. (Opp, Reference Opp1990). If social influence was not already triggered by intentions, its field relevance could be weaker. Although reacting to others’ actual behavior and outcomes is less risky, this allows for confounding factors like others’ ex post evaluations and revisions of prior intentions, which may (or may not) be affected by hindsight biases (Dahlberg, Reference Dahlberg1979).
Distinguishing purely intention-based social influence, similar to learning what neighbors or other peers intend to do, requires time delay between planning and realization.Footnote 2 To be effective, however, others’ intentions should be easily recognized. Rather than by field data we, therefore, analyze experimentally purely intention-based social influence in situations involving social and strategic interaction. More specifically, our focus is on how the median intention of one’s reference group affects individual behavior in Ultimatum and Impunity games. In the Ultimatum Game, a proposer makes a take-it-or-leave-it offer to a responder about how to split a pie, which can be accepted as is, or rejected. When rejected, both the proposer and the responder earn zero. When a responder rejects an offer in the Impunity Game, instead, the proposer keeps the difference between the pie and her/his offer, irrespective of the responder decision. In the Impunity Game, therefore, strategic considerations about the responder’s behavior are less relevant for the proposer.
Confirming intention-based social influence for a single type of game could be risky, as game-specific aspects may weaken or strengthen the effect. Therefore, as a minimal step to confirm robust findings, we implement a
![]() factorial experimental design varying: (i) the games’ order, first Ultimatum (UG) then Impunity (IG), or vice versa; and (ii) the strategy vector dimensionality, that are uni-dimensional or bi-dimensional. Across all conditions, participants choose a vector of choices playing in either role (i.e., proposer or responder), which is randomly assigned after their decision is made. When strategies are bi-dimensional, a participant can freely choose an offer as a proposer and an acceptance threshold as a responder. When strategies are uni-dimensional, participants have to choose an offer complementary to the acceptance threshold, i.e., the sum of the offer and the threshold must add up to the size of the pie.
factorial experimental design varying: (i) the games’ order, first Ultimatum (UG) then Impunity (IG), or vice versa; and (ii) the strategy vector dimensionality, that are uni-dimensional or bi-dimensional. Across all conditions, participants choose a vector of choices playing in either role (i.e., proposer or responder), which is randomly assigned after their decision is made. When strategies are bi-dimensional, a participant can freely choose an offer as a proposer and an acceptance threshold as a responder. When strategies are uni-dimensional, participants have to choose an offer complementary to the acceptance threshold, i.e., the sum of the offer and the threshold must add up to the size of the pie.
By informing participants about the median intention of their reference group, we study how their behavior reacts to this information. We induced group identity by randomly assigning individuals to groups which are minimally identified by colors (see Tajfel, Reference Tajfel1970). Using the minimal group paradigm, we focus on a worst-case scenario for confirming purely intention-based social influence, and for rendering others’ intentions relevant (the others belong to the same group) but not decisive (one cannot be sure about the intention of those whom s/he will interact with). Participants privately choose their intentions about what to offer and what to accept, then learn about the median intention(s) of their own group, and finally, based on this information, decide. Participants learn about their (randomly selected) actual role (i.e., proposer or responder) only at the very end of the experiment, to avoid any feedback effect. For the same reason, participants’ payoff is determined by picking one of the four possible experimental phases, and disclosed only at the end of the experiment.
Our design differs from the related research of Di Cagno et al. (Reference Di Cagno, Galliera, Güth and Panaccione2018). While they also study the effect of individual intentions in dyadic sharing games, they only let one individual adjust her decision, based on information about the other’s intention. In our setup, each individual group member, instead, observes the median intention of her reference group before playing. This design limits the possibilities for strategic manipulation because individuals declare their intentions without knowing who they will be interacting with within the group. So, it is unlikely to strategically state intentions, especially in Impunity play which should be more immune to strategic considerations.Footnote 3
While bi-dimensional IG elicits mainly intrinsic fairness, the more strategic UG involves strategic reasoning that may weaken and even crowd out intrinsic fairness concerns.Footnote 4 Even when being only interested in own payoff, belief-based social influence may be relevant in UG but is unlikely in IG, whose proposers get what they demand. Both games are often experimentally analyzed but rarely with uni-dimensional strategy vectors. In this case, we expect strategic considerations to be even more pronounced than in the bi-dimensional case. This is because, for example, reducing the offer to achieve social conformity automatically increases the acceptance threshold, necessitating higher offers. Given that the strategy space in uni-dimensional games is more constrained, participants place greater emphasis on strategic thinking and find it optimal to mix their strategies at equilibrium.
According to our data, social influence is role and game dependent. Bi-dimensionality encourages more opportunism compared to uni-dimensionality which requires more thorough reasoning for both roles due to the imposed consistency in offering and responding. In UG, one mainly tries to avoid conflict, whereas in IG, proposer opportunism can freely unfold and is enhanced by social influence.Footnote 5 Social influence in case of uni-dimensionality (one proposes and expects fair agreements in the private phase and rarely changes one’s mind after learning about the group median) differs from the one in the bi-dimensional case, which reveals more game dependence: after observing the group median offer and threshold, participants substantially increase their offer relative to their own intentions in the bi-dimensional UG, whereas they decrease it in the bi-dimensional IG. No significant effect emerges on the acceptance thresholds. Altogether, we confirm social influence as harmonizing behavior, but not across all conditions.
By varying the game, we explore whether the effect of bi-dimensionality depends on sanctioning power. Even in the usual bi-dimensional IG and UG participants can voluntarily restrict themselves to uni-dimensional intentions and choice behavior. By our design, voluntary uni-dimensional group intentions are not excluded but very unlikely (see already Güth et al., Reference Güth, Schmittberger and Schwarze1982; Güth and Kocher, Reference Güth and Kocher2014).
We structure the paper as follows: Section 2 illustrates the design of the experiment, its theoretical and behavioral predictions, and its implementation in the lab. In Sect. 3, we present and analyze the data of the different experimental conditions, which are further explored by regression analysis in Sect. 4. Finally, Sect. 5 concludes and connects our results to the relevant literature.
2 The experiment
We summarize the design of our experiment in Table 1, where we vary the strategic dimensionality available to participants, and the order of play of the two games. Strategy dimensionality refers both to intentions and choices: like in one-population evolutionary games, each participant acts in both roles, namely “proposer” and “responder.” We confront the standard bi-dimensional case (one freely chooses an offer as a proposer and an acceptance threshold as a responder) with the uni-dimensional one, where the offer and the acceptance threshold must add up to the size of the pie.
Table 1
![]() -factorial between-subjects design varying dimensionality and sequence of game types
-factorial between-subjects design varying dimensionality and sequence of game types

|
Strategy dimensionality |
UG-IG sequence |
IG-UG sequence |
|---|---|---|
|
Uni-dimensional |
Condition 1 |
Condition 2 |
|
Bi-dimensional |
Condition 3 |
Condition 4 |
Endowed with this design, we now provide a formal description of the games.
2.1 The experimental protocol
Basics Two participants, one proposer X and one responder Y, can share a positive monetary reward, the “pie”
![]() which, in the experiments, we set to
which, in the experiments, we set to
![]() . Role X offers to Y an integer amount y with
. Role X offers to Y an integer amount y with
![]() . Role Y can accept or reject the offer y by stating an acceptance threshold
. Role Y can accept or reject the offer y by stating an acceptance threshold
![]() , with
, with
![]() , rendering only offers
, rendering only offers
![]() acceptable. Rejection, i.e., non-acceptance, implies in ultimatum games (UG) that X and Y each earn 0, while in impunity games (IG) that proposer X earns
acceptable. Rejection, i.e., non-acceptance, implies in ultimatum games (UG) that X and Y each earn 0, while in impunity games (IG) that proposer X earns
![]() and only Y receives 0.
and only Y receives 0.
We experimentally employ the strategy vector method: every participant chooses an offer y in role X and an acceptance threshold
![]() in role Y. In the uni-dimensional condition, participants must choose y and
in role Y. In the uni-dimensional condition, participants must choose y and
![]() such that
such that
![]() .
.
The experiment implements IG as non-private impunity—meaning that X is informed whether Y has accepted and collected the offer y (Yamagishi et al., Reference Yamagishi, Horita, Takagishi, Shinada, Tanida and Cook2009). In the bi-dimensional condition, solution behavior of IG in weakly dominant strategies entails
![]() , the smallest positive amount, and
, the smallest positive amount, and
![]() , i.e., to accept all (positive) offers.Footnote 6 In UG, once repeated elimination of weakly dominated strategies also yields
, i.e., to accept all (positive) offers.Footnote 6 In UG, once repeated elimination of weakly dominated strategies also yields
![]() . Also other UG-equilibria requiring
. Also other UG-equilibria requiring
![]() with
with
![]() are less convincing since
are less convincing since
![]() is weakly dominated.
is weakly dominated.
In the uni-dimensional condition, in the UG, the only symmetric equilibrium in pure strategies entails
![]() , which yields, in expectation, the same individual payoff
, which yields, in expectation, the same individual payoff
![]() to both players. In the IG instead, players optimally mix their offer between two equilibrium pure strategies: that where, as a proposer, one offers
to both players. In the IG instead, players optimally mix their offer between two equilibrium pure strategies: that where, as a proposer, one offers
![]() (and demands
(and demands
![]() ), and the other where the offer is
), and the other where the offer is
![]() .
.
Let us now formally derive predictions about the uni-dimensional case, for both games. For UG, with random role assignment, the expected payoff of a player
![]() writes as
writes as
with
![]() being the indicator function equal to one if the condition in curly brackets is verified, and zero otherwise. It is easy to verify that the symmetric strategy vectors
being the indicator function equal to one if the condition in curly brackets is verified, and zero otherwise. It is easy to verify that the symmetric strategy vectors
![]() form an equilibrium that yields, in expectation,
form an equilibrium that yields, in expectation,
![]() for each party.
for each party.
To see why, note that when
![]() , the expected payoff of either party is
, the expected payoff of either party is
![]() , and that an asymmetric strategy vector
, and that an asymmetric strategy vector
![]() cannot yield more. Consider, for example, a unilateral deviation
cannot yield more. Consider, for example, a unilateral deviation
![]() . In this case, player i would only earn
. In this case, player i would only earn
![]() as proposer and
as proposer and
![]() as responder, since the acceptance threshold
as responder, since the acceptance threshold
![]() is smaller than j’s offer
is smaller than j’s offer
![]() . This deviation would be profitable if
. This deviation would be profitable if
which is true if and only if
![]() , a contradiction. Similarly, choosing
, a contradiction. Similarly, choosing
![]() is also not a profitable deviation. In this case, i earns zero as proposer since i’s offer is lower than j’s acceptance threshold, and earns zero as responder since j’s offer is lower than i’s acceptance threshold. Therefore, any deviation from
is also not a profitable deviation. In this case, i earns zero as proposer since i’s offer is lower than j’s acceptance threshold, and earns zero as responder since j’s offer is lower than i’s acceptance threshold. Therefore, any deviation from
![]() is not profitable for either player.
is not profitable for either player.
Because our experimental design restricts offers and thresholds to be chosen among integer numbers, however, individuals are unable to offer
![]() . We therefore expect individuals to mix their offer around
. We therefore expect individuals to mix their offer around
![]() , that is between
, that is between
![]() and
and
![]() .Footnote 7 For the sake of clarity, let us formally derive the mixed strategy equilibrium in the uni-dimensional condition using the following matrix representation for the UG case (Table 2):
.Footnote 7 For the sake of clarity, let us formally derive the mixed strategy equilibrium in the uni-dimensional condition using the following matrix representation for the UG case (Table 2):
Table 2 Mixed strategy equilibrium derivation, uni-dimensional UG

|
j-player |
|||
|---|---|---|---|
|
|
|
||
|
i-player |
|
0, 0 |
11, 10 |
|
|
10, 11 |
10.5, 10.5 |
|
There are two pure-strategy equilibrium, that is
![]() and
and
![]() . Let p and q be the probability of offering
. Let p and q be the probability of offering
![]() for player i and j, respectively. At equilibrium, player i equates the expected payoff obtained offering
for player i and j, respectively. At equilibrium, player i equates the expected payoff obtained offering
![]() with that obtained offering
with that obtained offering
![]() , that is
, that is
![]() . By symmetry, therefore, both i and j play the strategy vector
. By symmetry, therefore, both i and j play the strategy vector
![]() with probability
with probability
![]() .
.
Also in the IG, unlike the bi-dimensional case, there are multiple equilibria in pure strategies. In this case, player i and player j solve the following (Table 3):
Table 3 Mixed strategy equilibrium derivation, uni-dimensional IG

|
j-player |
|||
|---|---|---|---|
|
|
|
||
|
i-player |
|
5.5, 5.5 |
11, 10 |
|
|
10, 11 |
10.5, 10.5 |
|
By applying the same logic used for the UG, we can easily confirm that the mixed strategy equilibrium results in the offer
![]() being made with a probability of
being made with a probability of
![]() . This aligns with the intuition that offers tend to be higher in the UG than in the IG, primarily due to individuals’ aversion to entering into conflict and potentially ending up with nothing. Hence, the probability of offering 11 is higher in UG (20/21) compared to IG (9/10).
. This aligns with the intuition that offers tend to be higher in the UG than in the IG, primarily due to individuals’ aversion to entering into conflict and potentially ending up with nothing. Hence, the probability of offering 11 is higher in UG (20/21) compared to IG (9/10).
Social influence How can the group affect via its median intentions the individual strategy vector choices
![]() in the bi-dimensional and
in the bi-dimensional and
![]() in the uni-dimensional case? In the experiment, groups of four participants are formed randomly and minimally identified by a color (black, white, orange, yellow, blue and green). Thus, we do not study social influence via social norms like Krupka and Weber (Reference Krupka and Weber2009) or via reacting to being (un)equal (e.g., Hennig-Schmidt et al., Reference Hennig-Schmidt, Irlenbusch, Rilke and Walkowitz2018). Instead group members only share the “same color” and are aware that they are only one of four with that “color.”
in the uni-dimensional case? In the experiment, groups of four participants are formed randomly and minimally identified by a color (black, white, orange, yellow, blue and green). Thus, we do not study social influence via social norms like Krupka and Weber (Reference Krupka and Weber2009) or via reacting to being (un)equal (e.g., Hennig-Schmidt et al., Reference Hennig-Schmidt, Irlenbusch, Rilke and Walkowitz2018). Instead group members only share the “same color” and are aware that they are only one of four with that “color.”
Social influence is based only on stated intentions, more specifically on the group’s “median intended offer”,
![]() , and “median intended acceptance threshold”,
, and “median intended acceptance threshold”,
![]() . For each group of four, we compute the mean of the two intermediate intentions, i.e., intended offer (resp. threshold), and refer to it as “median” offer (resp. threshold).Footnote 8 After all four participants stated their intentions, we informed each group member about the “median” intentions of their group before finally asking them to decide about
. For each group of four, we compute the mean of the two intermediate intentions, i.e., intended offer (resp. threshold), and refer to it as “median” offer (resp. threshold).Footnote 8 After all four participants stated their intentions, we informed each group member about the “median” intentions of their group before finally asking them to decide about
![]() , or
, or
![]() , unaware of whom of the three others they would play the game with. Social influence is measured by how strongly group members react to their group’s median intentions. Therefore, a participant can only influence others through the median, and knowing that also the other group members react to the same intentions.
, unaware of whom of the three others they would play the game with. Social influence is measured by how strongly group members react to their group’s median intentions. Therefore, a participant can only influence others through the median, and knowing that also the other group members react to the same intentions.
Timing Participants play each game in two phases: In the first, private play, they play without knowing the median intention of their reference group. In the second, social play, they learn the median intention of their group before making their choices.
In each phase, game playing proceeds as follows:
1. random pair formation;
2. strategy vector choices by either pair member, determining the outcome and individual payoffs;
3. random role assignment.
For each phase, participants play UG followed by IG or vice versa. Only after both games, participants are informed about their role and payoffs.
Notice that, unlike the second phase, participants play the game in the first phase without knowing the median intentions (
![]() ), respectively
), respectively
![]() . While the first phase establishes already group membership, information on payoffs is not revealed yet. So, the design avoids learning or order-of-play effects in the first game played in the sequence (either UG or IG). We test that there are no statistically significant differences between the two sequences of games in the results section. Summing up, Fig. 1 describes the timeline of each experiment, which is the same for all conditions (i.e., both game types, private and social play, uni- or bi-dimensional strategy vector).
. While the first phase establishes already group membership, information on payoffs is not revealed yet. So, the design avoids learning or order-of-play effects in the first game played in the sequence (either UG or IG). We test that there are no statistically significant differences between the two sequences of games in the results section. Summing up, Fig. 1 describes the timeline of each experiment, which is the same for all conditions (i.e., both game types, private and social play, uni- or bi-dimensional strategy vector).

Fig. 1 Timeline of the experiments for each game, UG and IG, and uni- or bi-dimensional strategy vector elicitation
2.2 Behavioral predictions and research questions
Behaviorally, the actual strategy vector choices in the second phase to which we refer as “social” play, can be affected:
(i) by one’s first phase strategy vector (
 ) or
) or
 to which we refer as “private” intentions;
to which we refer as “private” intentions;(ii) by own second phase or “social” intentions (
 ) or
) or
 as well as
as well as(iii) by the median second phase intentions (
 ) or
) or
 .
.
Effects of (i) and (ii) could result from wanting to be consistent, i.e., by not at all or only slightly adjusting one’s final vector choice
![]() or
or
![]() in the second phase. This could signal a desire for self-consistency in the form of stability to external influence, for instance due to an ego-defensive attitude against social influence in the attempt to avoid cognitive dissonance (see Festinger and Hutte, Reference Festinger and Hutte1954). Social influence would be captured by effects of (iii). Of course, deviations from own intentions only count as social influence when tending toward median intentions, in the bi-dimensional case at least in one dimension.
in the second phase. This could signal a desire for self-consistency in the form of stability to external influence, for instance due to an ego-defensive attitude against social influence in the attempt to avoid cognitive dissonance (see Festinger and Hutte, Reference Festinger and Hutte1954). Social influence would be captured by effects of (iii). Of course, deviations from own intentions only count as social influence when tending toward median intentions, in the bi-dimensional case at least in one dimension.
We expect and predict that favorable social influence will trigger opportunism, e.g., learning that lower offers are intended by others might induce individuals to offer less. This is particularly true in UG, where others’ intentions can inform also how to avoid conflict: if acceptance thresholds are seemingly high, one better offers more as a proposer. It is also possible, however, that social influence operates in an opposite way. For example, this may occur when an individual makes an offer that is lower than what is believed socially acceptable, but then observes a lower than expected median intended offer. This observation may induce the individual to further reduce the offer.
Differentiating between bi-dimensional and uni-dimensional games can introduce additional complexities. In the bi-dimensional variant, strategic considerations tend to reinforce social conformity: lower proposed offers call for lower actual thresholds in both game types, and larger proposed thresholds inspire higher offers in the bi-dimensional UG.
The influence of strategic motive becomes even stronger in uni-dimensional games, but interestingly, it moves in a direction that contradicts social conformity. Lower proposed offers force players to increase their thresholds (as offers and threshold must add to the pie size), triggering a consequent rise in offers. This effect is present in the UG but not in the IG, as proposers in the IG do not bear the risk of conflict.
The uni-dimensional equilibrium predictions suggest that individuals are likely to mix their offers around
![]() . However, it is challenging to establish definitive predictions about how median intentions will impact the equilibrium behavior of proposers and respondents. For this reason, we have developed the following exploratory research questions that we aim to evaluate in the experiment:
. However, it is challenging to establish definitive predictions about how median intentions will impact the equilibrium behavior of proposers and respondents. For this reason, we have developed the following exploratory research questions that we aim to evaluate in the experiment:
Research Question 1 (RQ1) : What is the impact of observing others’ median intended offers and thresholds on individual behavior of proposers and respondents?
Research Question 2 (RQ2) : Does the influence of median proposed offers and thresholds remain consistent across different games and conditions of strategic dimensionality?
2.3 Implementation
We recruited 128 participants from a pool of undergraduate students (60% females) from the faculties of Economics (39.06%), Engineering, Physics or Math (14.84%), Law or Political Science (12.5%) or other majors (33.59%) at the University of Siena (Italy) using hroot (Bock et al., Reference Bock, Baetge and Nicklisch2014). No subject participated in more than one session. The experiment was programmed and conducted using z-Tree (Fischbacher, Reference Fischbacher2007).
An experimenter read the instructions aloud and answered questions privately before starting the experiment.Footnote 9 Since both paired participants submit a strategy vector for both games and pairs were matched only after private and social play, we obtained
![]() strategy vectors per group with four participants. Due to 32 groups, our dataset contains
strategy vectors per group with four participants. Due to 32 groups, our dataset contains
![]() strategy vectors which we analyze globally and treatment-wise.
strategy vectors which we analyze globally and treatment-wise.
As participants decide how to split
![]() at each phase, the software randomly selects for each participant, at the end of the experiment, one of the payoffs resulting from their play as the final payment. Participants received in cash, anonymously, the equivalent payoff in euros (i.e., 1 Experimental Currency Unit = 1 euro).
at each phase, the software randomly selects for each participant, at the end of the experiment, one of the payoffs resulting from their play as the final payment. Participants received in cash, anonymously, the equivalent payoff in euros (i.e., 1 Experimental Currency Unit = 1 euro).
3 Descriptive data analysis and mean results
To compare behavior across experimental conditions, Table 4 reports summary statistics for the actual offers (y) and thresholds (
![]() ). Columns (1) and (2) (resp. (3) and (4)) report average uni-dimensional (resp. bi-dimensional) strategy vector choices. Panel A (resp. Panel B) reports the average uni- versus bi-dimensional strategy vectors for UG and IG, during the private (resp. social) phase of the experiments. Average strategy vectors across experimental conditions are compared by Wilcoxon–Mann–Whitney tests. We report the p values of these tests comparing the uni-dimensional and the bi-dimensional choices in column (5), and the comparisons between the UG and IG at the bottom of Panels A and B in Table 4.
). Columns (1) and (2) (resp. (3) and (4)) report average uni-dimensional (resp. bi-dimensional) strategy vector choices. Panel A (resp. Panel B) reports the average uni- versus bi-dimensional strategy vectors for UG and IG, during the private (resp. social) phase of the experiments. Average strategy vectors across experimental conditions are compared by Wilcoxon–Mann–Whitney tests. We report the p values of these tests comparing the uni-dimensional and the bi-dimensional choices in column (5), and the comparisons between the UG and IG at the bottom of Panels A and B in Table 4.
Participants offer significantly less in the bi-dimensional case, regardless of the game played and the phase of the experiment. This likely indicates that the uni-dimensional condition, by forcing participants to be consistent, induces them to increase their offers. At the same time, participants decrease their acceptance thresholds in the bi-dimensional condition (see column (5) of Table 4). This perhaps results from a larger choice set, which allows participants to express more freely their preferences when being proposer or responder.
It is interesting to compare UG and IG behavior across the private and social phases. In the private phase, without any feedback from the reference group, individuals offer more in UG than in IG. Also during the social phase, possibly fearing sanctioning by the counterpart, participants’ offers are higher in UG with respect to IG and, in particular, in the uni-dimensional condition. This may be further evidence that imposed consistency induces participants to attempt more an agreement with their counterpart.
Finally, in Panel C, we report the p values from Wilcoxon matched-pairs signed-rank tests, which we use to compare the private and social phases. Recall that the same individuals participate in these phases during the beginning and end of the experiment, respectively (see Fig. 1). Our findings do not reveal a significant overall effect from revealing median intentions, which might hide effects that are happening at an individual level.Footnote 10
Table 4 Panel A (resp. B) reports summary statistics for the actual average group offers y and minimum acceptance thresholds
![]() referring to the private (resp. social) phase of the experiment, with uni-dimensional strategies in columns (1) and (2), and bi-dimensional strategies in columns (3) and (4)
referring to the private (resp. social) phase of the experiment, with uni-dimensional strategies in columns (1) and (2), and bi-dimensional strategies in columns (3) and (4)

|
Panel A: |
Uni-dimensional |
Bi-dimensional |
|||
|---|---|---|---|---|---|
|
Private phase |
(1) |
(2) |
(3) |
(4) |
(5) |
|
UG (
|
Mean |
SD |
Mean |
SD |
Uni vs Bi |
|
y |
12.47 |
2.93 |
10.92 |
3.43 |
0.00 |
|
|
8.53 |
2.93 |
7.41 |
3.79 |
0.00 |
|
IG (
|
Mean |
SD |
Mean |
SD |
|
|
y |
11.64 |
3.22 |
9.67 |
3.38 |
0.00 |
|
|
9.36 |
3.22 |
7.36 |
3.61 |
0.00 |
|
UG vs IG (y) |
0.01 |
0.00 |
|||
|
UG vs IG (
|
0.01 |
0.97 |
|||
|
Panel B: |
Uni-dimensional |
Bi-dimensional |
|||
|---|---|---|---|---|---|
|
Social phase |
(1) |
(2) |
(3) |
(4) |
(5) |
|
UG (
|
Mean |
SD |
Mean |
SD |
Uni vs Bi |
|
y |
12.19 |
2.89 |
11.23 |
3.31 |
0.00 |
|
|
8.81 |
2.89 |
7.34 |
3.58 |
0.00 |
|
IG (
|
Mean |
SD |
Mean |
SD |
|
|
y |
11.03 |
3.19 |
10.09 |
4.24 |
0.00 |
|
|
9.97 |
3.19 |
6.97 |
3.64 |
0.00 |
|
UG vs IG (y) |
0.00 |
0.03 |
|||
|
UG vs IG (
|
0.00 |
0.47 |
|||
|
Panel C: |
Uni-dimensional |
Bi-dimensional |
|||
|---|---|---|---|---|---|
|
UG |
|||||
|
Private vs Social (y) |
0.33 |
0.27 |
|||
|
Private vs Social (
|
0.33 |
0.92 |
|||
|
IG |
|||||
|
Private vs Social (y) |
0.45 |
0.21 |
|||
|
Private vs Social (
|
0.45 |
0.45 |
|||
p values of Wilcoxon–Mann–Whitney tests comparing uni-dimensional versus bi-dimensional strategy vector elicitations are reported in column (5). For each comparison,
![]() . At the bottom of Panel A (resp. B), we report p values of Wilcoxon matched-pairs signed-rank tests, comparing the equality of average group offers and minimum acceptance thresholds between UG and IG, during the private (resp. social) phase of the experiment. Panel C, finally, reports the p values of Wilcoxon matched-pairs signed-rank tests for the comparison between the private and social phase, for each experimental condition
. At the bottom of Panel A (resp. B), we report p values of Wilcoxon matched-pairs signed-rank tests, comparing the equality of average group offers and minimum acceptance thresholds between UG and IG, during the private (resp. social) phase of the experiment. Panel C, finally, reports the p values of Wilcoxon matched-pairs signed-rank tests for the comparison between the private and social phase, for each experimental condition
Result 1: For either game type, participants significantly adjust offers and acceptance thresholds downwards in case of bi-dimensionality.
The low significance of social influence and the limited behavioral alignment may partly be due to inducing group identity only by the minimal group paradigm, and by abstaining from out-group competition. As anticipated, however, the lack of observable evidence for social influence on aggregate behavior could potentially mask effects that work at the individual level. To explore this possibility, we will now focus on analyzing the impact of social influence while accounting for individual intentions.
To test the direction of intention-based influence, in Fig. 2, we show the impact of median intentions on the average discrepancies between intended and actual actions. This is depicted for each type of game and strategy dimensionality. The figure is arranged with offers at the top and thresholds at the bottom, showing their respective effects. Light and dark gray indicate private (i.e., no feedback) and social (i.e., median feedback) phase of the experiment, respectively.
In both UG and IG, participants significantly modify their intended offers: in UG, they increase their actual offers in the social game phase, whereas in IG, they decrease actual offers. Other differences between private and social play are not statistically significant.
Result 2: Actual offers differ significantly from own intentions, with the average difference changing from null to positive in UG when comparing private and social play. For IG, the small positive difference becomes negative and larger. Beyond this, social play seems to have no significant effect.
Figure 2 reveals negative deviations of actual from intended choices for IG. The game-dependency of average offer adjustment,
![]() , illustrates an interesting interaction between “second thoughts” and “sanctioning power” when “second thoughts” mean to switch from emotion-triggered intentions to more thoroughly deliberated actual behavior, which lets one become more opportunistic. This would explain the IG effects. In UG, however, proposer opportunism runs the risk of losing everything and “second thoughts” may even trigger more generous offers.Footnote 11
, illustrates an interesting interaction between “second thoughts” and “sanctioning power” when “second thoughts” mean to switch from emotion-triggered intentions to more thoroughly deliberated actual behavior, which lets one become more opportunistic. This would explain the IG effects. In UG, however, proposer opportunism runs the risk of losing everything and “second thoughts” may even trigger more generous offers.Footnote 11

Fig. 2 Average differences between actual and intended offers (
![]() ) (resp. threshold (
) (resp. threshold (
![]() )) in private and social plays. The left (resp. right) panel presents averages from the UG (resp. IG) phase. p values of Wilcoxon matched-pairs signed-rank tests between private and social plays are reported across the two bars
)) in private and social plays. The left (resp. right) panel presents averages from the UG (resp. IG) phase. p values of Wilcoxon matched-pairs signed-rank tests between private and social plays are reported across the two bars
Participants significantly adjust their UG (resp. IG) offer upwards (resp. downwards) whereas in both, UG and IG, they adjust their acceptance thresholds downwards, albeit with lower statistical significance. The altruistic sanctioning threat of UG is most clearly obvious in bi-dimensional social play. Compared to intentions, offers are enhanced and acceptance thresholds reduced, i.e., in both roles one tries to avoid conflict. The different effects for IG, compared to UG (see Fig. 2), suggest self-serving behavior rather than fairness concerns. All statistically significant differences apply only to the bi-dimensional case.
Result 3: Social interaction induces participants to adjust actual offers to intended ones: upward (resp. downward) in UG (resp. IG) but only in the bi-dimensional conditions.
4 Regression analysis
To econometrically validate and further investigate the previous findings, linear regression analyses will control different conditions of the experiment.Footnote 12
Social interaction Table 5 reports in Panel A (resp. Panel B), the estimated coefficient of Social Influence in regression models with the proposer offer y (resp. responder acceptance threshold
![]() ) as dependent variable, with p values in parentheses. To account for possible interdependence across observations, we clustered standard errors at the reference-group-session level. All regressions also control for the game sequence condition, the median intended offer, and the median intended threshold, and we report their respective coefficients. Regressions in Panel A (resp. Panel B) also control for the individual own intended offer (resp. minimum accepted threshold).
) as dependent variable, with p values in parentheses. To account for possible interdependence across observations, we clustered standard errors at the reference-group-session level. All regressions also control for the game sequence condition, the median intended offer, and the median intended threshold, and we report their respective coefficients. Regressions in Panel A (resp. Panel B) also control for the individual own intended offer (resp. minimum accepted threshold).
Table 5 This table reports, in Panel A (resp. Panel B), the estimated coefficient of Social Influence in a OLS model with individual offers (resp. acceptance thresholds) as dependent variable, for each of the experimental conditions

|
Panel A: Proposer’s offer |
(1) |
(2) |
(3) |
(4) |
|---|---|---|---|---|
|
Social influence |
0.069 |
|
0.394 |
|
|
(0.719) |
(0.425) |
(0.024) |
(0.005) |
|
|
Median intended offer |
|
0.061 |
0.017 |
0.159 |
|
(0.121) |
(0.725) |
(0.853) |
(0.029) |
|
|
Median intended threshold |
|
|
||
|
(0.073) |
(0.140) |
|||
|
Own intention |
0.902 |
0.755 |
0.973 |
0.927 |
|
(0.000) |
(0.000) |
(0.000) |
(0.000) |
|
|
UG-IG sequence |
0.196 |
|
0.028 |
0.065 |
|
(0.285) |
(0.602) |
(0.884) |
(0.746) |
|
|
Constant |
2.571 |
2.164 |
0.985 |
|
|
(0.033) |
(0.371) |
(0.234) |
(0.659) |
|
|
Observations |
128 |
128 |
128 |
128 |
|
R-squared |
0.854 |
0.703 |
0.898 |
0.886 |
|
Panel B: Responder’s threshold |
(1) |
(2) |
(3) |
(4) |
|---|---|---|---|---|
|
Social influence |
|
0.303 |
|
|
|
(0.719) |
(0.425) |
(0.322) |
(0.125) |
|
|
Median intended offer |
0.128 |
|
0.043 |
0.088 |
|
(0.121) |
(0.725) |
(0.285) |
(0.025) |
|
|
Median intended threshold |
0.028 |
|
||
|
(0.605) |
(0.503) |
|||
|
Own intention |
0.902 |
0.755 |
0.871 |
0.869 |
|
(0.000) |
(0.000) |
(0.000) |
(0.000) |
|
|
UG-IG sequence |
|
0.158 |
0.207 |
0.485 |
|
(0.285) |
(0.602) |
(0.193) |
(0.084) |
|
|
Constant |
|
2.991 |
0.208 |
0.297 |
|
(0.623) |
(0.186) |
(0.734) |
(0.504) |
|
|
Observations |
128 |
128 |
128 |
128 |
|
R-squared |
0.854 |
0.703 |
0.909 |
0.842 |
|
Strategies |
Uni-dimensional |
Uni-dimensional |
Bi-dimensional |
Bi-dimensional |
|
Game |
Ultimatum |
Impunity |
Ultimatum |
Impunity |
Standard errors are clustered at the group-session level. p values are reported in parentheses
Interestingly, the results show that social influence is game dependent, as it induces participants to adjust upwards their offers in UG but downwards in IG, and that others’ intentions are important but only when controlling for individuals’ own intentions. That the coefficients have different signs in UG and IG further suggests that intentions are used by participants to signal what is socially desirable in a different way. In UG, social influence complements the strategic pressure of possible conflict and let individuals increase their offers. In IG, instead, intentions signal to the group that the socially desirable offer is likely lower than initially expected and, therefore, induces individuals to adjust offers downwards. Notice that these differences are statistically significant only in the bi-dimensional condition, where participants are left free to behave as their intrinsic preferences suggest. Moreover, the coefficient for the median intended offer is statistically significant only for the IG, where the desire for conformity may be higher than in the more strategic UG.
In the bi-dimensional UG case, we found an unexpected negative correlation between offers and the median intended threshold, although with low statistical significance (p value greater than 0.05). This may suggest a potential “costly counter-punishment” mechanism where proposers lower offers if they perceive the median threshold as too high compared to their expectation.Footnote 13
Individual deviations Table 6 reports, in Panel A (resp. Panel B) multivariate OLS regressions with differences between actual and intended individual offers (resp. thresholds). Columns (1) and (2) report regression results under the uni-dimensional case, for UG and IG respectively. Columns (3) and (4) report estimates only for the bi-dimensional condition, again for UG and IG respectively.
Table 6 This table reports, in Panel A (resp. Panel B), the estimated coefficient of Social Influence in a OLS model with individual deviations from intended offers (resp. minimum accepted thresholds) as dependent variable, for each of the experimental conditions

|
Panel A: Individual deviation from intended offer |
(1) |
(2) |
(3) |
(4) |
|---|---|---|---|---|
|
Social influence |
0.115 |
|
0.395 |
|
|
(0.559) |
(0.580) |
(0.023) |
(0.004) |
|
|
Median intended offer |
|
|
|
0.088 |
|
(0.027) |
(0.454) |
(0.891) |
(0.031) |
|
|
Median intended threshold |
|
|
||
|
(0.069) |
(0.136) |
|||
|
UG-IG sequence |
0.177 |
|
0.026 |
0.056 |
|
(0.345) |
(0.622) |
(0.890) |
(0.789) |
|
|
Constant |
2.512 |
1.866 |
0.969 |
|
|
(0.038) |
(0.467) |
(0.238) |
(0.768) |
|
|
Observations |
128 |
128 |
128 |
128 |
|
R-squared |
0.068 |
0.019 |
0.063 |
0.071 |
|
Panel B: Individual deviation from intended threshold |
(1) |
(2) |
(3) |
(4) |
|---|---|---|---|---|
|
Social influence |
|
0.203 |
|
|
|
(0.559) |
(0.580) |
(0.231) |
(0.120) |
|
|
Median intended offer |
0.223 |
0.160 |
0.038 |
0.078 |
|
(0.027) |
(0.454) |
(0.317) |
(0.051) |
|
|
Median intended threshold |
|
|
||
|
(0.210) |
(0.028) |
|||
|
UG-IG sequence |
|
0.166 |
0.222 |
0.497 |
|
(0.345) |
(0.622) |
(0.153) |
(0.092) |
|
|
Constant |
|
|
0.059 |
0.270 |
|
(0.038) |
(0.467) |
(0.909) |
(0.579) |
|
|
Observations |
128 |
128 |
128 |
128 |
|
R-squared |
0.068 |
0.019 |
0.021 |
0.054 |
|
Strategies |
Uni-dimensional |
Uni-dimensional |
Bi-dimensional |
Bi-dimensional |
|
Game |
Ultimatum |
Impunity |
Ultimatum |
Impunity |
Standard errors are clustered at the group-session level
The coefficient of Social Influence is again statistically significant and positive for individual deviations from intended offers in the UG, while it is negative in the IG. This finding confirms the average treatment effect that in UG one adjusts the offer upward only when observing group median. While the positive effect of social interaction combined with UG is confirmed and reinforced in the bi-dimensional condition, individuals do not react in the same way in the uni-dimensional treatment. Whereas in the bi-dimensional treatment one offers more to avoid conflict, this is inhibited in the uni-dimensional case since higher offers automatically trigger lower acceptance thresholds.
When considering the difference between actual and intended acceptance thresholds, one overall reacts negatively to social influence, as confirmed by the negative—although not statistically significant—Social coefficient in columns (3) and (4), in line with the “second thought effect,” when switching from more emotional to more deliberative and opportunistic decision making (see also Cason and Mui, Reference Cason and Mui1998, for a discussion of this effect in the context of a sequential dictator game).
5 Final remarks
Our results shed light on the importance of purely intention-based social influence, which is less special than it may seem (see also Reference Cason and Mui1998). International agreements, for example to limit global warming, specify only what is signed so far, without verifying compliance. So, agreements specify only intentions to which one may or may not react.Footnote 14 In politics, political programs circulated before an election are designed to attract votes rather than representing reliable plans. Similarly, in the commercial sphere, acquiring companies declare how many employees they intend to keep in employment with little reliability for actual downsizing.
We narrowly analyzed social influence per se, i.e., without inter-group competition, in the sense of only being based on others’ intentions and not on their actual behavior (see Vega-Redondo, Reference Vega-Redondo1995; Charness and Sutter, Reference Charness and Sutter2012) for imitation. So, we let participants independently choose strategy vectors, and state own intentions before confronting them with those of others.Footnote 15
We have explored how participants with self-generated intentions are socially influenced only by the median intentions in their group. Additionally, we study the effect of others’ intentions in two different strategic conditions (UG vs. IG) and, in order to account for consistency in role-decisions, we confront the usual bi-dimensional with the uni-dimensional strategy vector elicitation. Altogether, we consider the bi-dimensional IG to be the best-case scenario for confirming purely intention-based influence. In this case, intention-based influence is not counteracted by strategic incentives, and there are fewer constraints on the action space.
Reassuringly, our results are in line with the theoretical predictions. We confirm statistically significant effects of information about median intentions in the sense of conformity seeking in IG, but not in UG. While in UG social influence positively affects offers, in IG it significantly reduces them. This consistently depends on the different motivations (strategic versus equity) which are often seen as the main drivers in these two different games (see e.g., Cooper and Kagel, Reference Cooper and Kagel2016).
Altogether, our results seem to reveal an interesting informative effect of social intentions on conformity, that only works in the bi-dimensional strategy vector elicitation condition, while it does not trigger more conformism or fairness in the uni-dimensional condition. Moreover, as we did not want to impose a specific structure for mechanisms underlying social influence, we did not explicitly model how others’ intentions map into individuals’ actual strategies. In this respect, it would be interesting to explore how median offer and median acceptance threshold, in the bi-dimensional condition, interact with each other. Understanding the determinants of the individual behavior in bi- and uni-dimensional condition could be an interesting topic of future research, especially with enough data about voluntary uni-dimensionality.
Supplementary Information
The online version contains supplementary material available at https://doi.org/10.1007/s40881-023-00147-1.
Acknowledgements
The replication material for the study is available at https://doi.org/10.3886/E172581V2. We gratefully acknowledge financial support from Webster University Geneva and University of Campania Luigi Vanvitelli. Our gratitude extends to two anonymous referees and, in particular, to editors Maria Bigoni, Dirk Engelmann, and Lionel Page for their invaluable inputs. We also thank Anna Conte, Gulen Karakoc, Marco Pagnozzi, Paolo Roberti, Tim Salmon, Krista Saral, and the 2019 LUISS Experimental Economics Workshop participants for their comments. Francesco Lomagistro and Roland Daguerre provided valuable research assistance.
Funding
Open access funding provided by Università degli Studi della Campania Luigi Vanvitelli within the CRUI-CARE Agreement. This article was funded by Università degli Studi della Campania Luigi Vanvitelli (Grant no. 2017\5926) and Webster University Geneva.


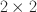

 2×2
2×2



 y̲
y̲
 y-y0
y-y0 y̲-y̲0
y̲-y̲0

