NILPOTENT SUBSPACES AND NILPOTENT ORBITS

Abstract

Let 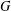$G$ be a semisimple complex algebraic group with Lie algebra 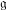$\mathfrak{g}$. For a nilpotent 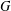$G$-orbit 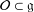${\mathcal{O}}\subset \mathfrak{g}$, let 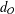$d_{{\mathcal{O}}}$ denote the maximal dimension of a subspace 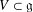$V\subset \mathfrak{g}$ that is contained in the closure of 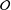${\mathcal{O}}$. In this note, we prove that 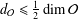$d_{{\mathcal{O}}}\leq {\textstyle \frac{1}{2}}\dim {\mathcal{O}}$ and this upper bound is attained if and only if 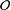${\mathcal{O}}$ is a Richardson orbit. Furthermore, if 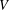$V$ is 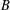$B$-stable and 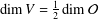$\dim V={\textstyle \frac{1}{2}}\dim {\mathcal{O}}$, then 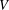$V$ is the nilradical of a polarisation of 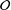${\mathcal{O}}$. Every nilpotent orbit closure has a distinguished 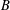$B$-stable subspace constructed via an 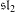$\mathfrak{sl}_{2}$-triple, which is called the Dynkin ideal. 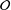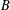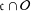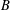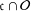We then characterise the nilpotent orbits ${\mathcal{O}}$ such that the Dynkin ideal (1) has the minimal dimension among all $B$-stable subspaces $\mathfrak{c}$ such that $\mathfrak{c}\cap {\mathcal{O}}$ is dense in $\mathfrak{c}$, or (2) is the only $B$-stable subspace $\mathfrak{c}$ such that $\mathfrak{c}\cap {\mathcal{O}}$ is dense in $\mathfrak{c}$.