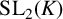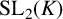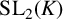BASIC NONARCHIMEDEAN JØRGENSEN THEORY

Abstract

We prove a nonarchimedean analogue of Jørgensen’s inequality, and use it to deduce several algebraic convergence results. As an application, we show that every dense subgroup of ${\mathrm {SL}_2}(K)$, where K is a p-adic field, contains two elements that generate a dense subgroup of ${\mathrm {SL}_2}(K)$, which is a special case of a result by Breuillard and Gelander [‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467]. We also list several other related results, which are well known to experts, but not easy to locate in the literature; for example, we show that a nonelementary subgroup of ${\mathrm {SL}_2}(K)$ over a nonarchimedean local field K is discrete if and only if each of its two-generator subgroups is discrete.

1 Introduction

In [13], Jørgensen developed a fundamental inequality that is a necessary condition for a nonelementary two-generator subgroup of ${\mathrm {SL}_2}(\mathbb {C})$ to be discrete (that is, a Kleinian group) and used it to study the algebraic convergence of Kleinian groups. Subgroups of ${\mathrm {SL}_2}(\mathbb {C})$ act by orientation-preserving isometries on hyperbolic 3-space [2], and this famous inequality has motivated many further studies of discrete groups that act on hyperbolic structures; see for instance [9, 11, 21]. Here we develop analogous results for subgroups of ${\mathrm {SL}_2}$ over nonarchimedean local fields that act by isometries and without inversion on a Bruhat–Tits tree [26, Ch. II, Section 1].

Let K be a nonarchimedean local field, that is, either a p-adic field (in other words, a finite extension of the p-adic numbers $\mathbb {Q}_p$ ) or the field of formal Laurent series $\mathbb {F}_q((t))$ . We use $T_K$ to denote the corresponding Bruhat–Tits tree, and we equip ${\mathrm {SL}_2}(K)$ with the subspace topology inherited from $K^4$ .

Our first result is a nonarchimedean analogue of Jørgensen’s inequality [13, Lemma 1]. This generalises [1, Theorem 4.2] and [23, Theorem 1.5] to discrete two-generator subgroups of ${\mathrm {SL}_2}(K)$ that do not have a fixed end.

Theorem A. Let K be a nonarchimedean local field with discrete valuation v. There exists a nonnegative constant $M_K$ such that, if $G=\langle A, B \rangle $ is a discrete subgroup of ${\mathrm {SL}_2}(K)$ that does not fix an end of $T_K$ , then

(1-1) $$ \begin{align} {\operatorname{min}}\{v(\mathrm{tr}^2(A)-4), v(\mathrm{tr}([A,B])-2) \} \le M_K. \end{align} $$

By a nonelementary subgroup of ${\mathrm {SL}_2}(K)$ , we mean a subgroup that does not stabilise a vertex, an end or a pair of ends of $T_K$ . In particular, Theorem A holds when G is nonelementary.

Using results from [9], we also obtain a more specialised version of Theorem A for discrete and nonelementary two-generator subgroups of ${\mathrm {SL}_2}(K)$ . As is done in [15] for the original statement of Jørgensen’s inequality, we additionally determine when equality occurs in this setting.

Theorem B. Let K be a nonarchimedean local field with discrete valuation v. Let $G=\langle A, B \rangle $ be a discrete and nonelementary subgroup of ${\mathrm {SL}_2}(K)$ . If $K=\mathbb {Q}_p$ , or G contains no elements of order p (where p is the characteristic of the residue field of K), then

(1-2) $$ \begin{align}{\operatorname{min}}\{v(\mathrm{tr}^2(A)-4), v(\mathrm{tr}([A,B])-2) \} \le 0. \end{align} $$

Moreover, equality occurs if and only if A is elliptic of finite order, B is hyperbolic and the fixed point set of A intersects the translation axis of B in a finite path of length equal to the translation length of B.

Remark 1.1. By [9, Theorems A and B], there are seven possible isomorphism classes for such a group G that achieves equality in (1-2). These isomorphism classes are identified in cases (f) and (g) of [9, Theorem A]. Furthermore, cases (b)–(d) of [9, Theorem A] describe the isomorphism classes for which the inequality (1-2) is strict.

We use Theorem A to obtain a nonarchimedean analogue of [2, Theorem 5.4.2]. Note that the assumption that the subgroup is nonelementary is necessary; see Example 6.1.

Proposition 1.2. A nonelementary subgroup of ${\mathrm {SL}_2}(K)$ is discrete if and only if each of its two-generator subgroups is discrete.

In many cases, we obtain the following stronger result, which is also well known to experts.

Proposition 1.3. Let G be a subgroup of $\mathrm {SL}_2(K)$ , where K is a nonarchimedean local field. If either $\mathrm {char }(K)=0$ , or $\mathrm {char }(K)=p>0$ and G contains no elements of order p, then G is discrete if and only if each of its cyclic subgroups are discrete.

Let $\Gamma $ and H be groups, and let $\{\phi _n:\Gamma \to G_n\}$ be a sequence of homomorphisms onto subgroups $G_n$ of H. If $\lim _{n \to \infty } \phi _n(\gamma )$ exists as an element of H for each $\gamma \in \Gamma $ , then we define the group $G = \{g \in H : g= \lim _{n \to \infty } \phi _n(\gamma ),\,\gamma \in \Gamma \}$ and say that the sequence of groups $\{G_n=\phi _n(\Gamma )\}$ converges algebraically to G. We also say that a sequence $\{a_n\}$ is eventually X if there exists an N such that the element $a_n$ is X for all $n\geq N$ .

We use Theorem A to deduce the following algebraic convergence results for subgroups of ${\mathrm {SL}_2}(K)$ . The first is a nonarchimedean analogue of [13, Theorem 1].

Theorem C. Let $\Gamma \le {\mathrm {SL}_2}(K)$ be discrete and nonelementary, and let $\{\phi _n:\Gamma \to G_n\}$ be a sequence of isomorphisms between $\Gamma $ and subgroups $G_n$ of ${\mathrm {SL}_2}(K)$ that are eventually discrete. If $\{G_n\}$ converges algebraically to G, then G is discrete and nonelementary, and the map $\phi : \Gamma \to G$ defined by $\phi (\gamma )=\lim _{n \to \infty } \phi _n(\gamma )$ is an isomorphism.

Remark 1.4. Theorem C does not require $\Gamma $ to be finitely generated.

We also give a nonarchimedean analogue of the main theorem of [16]. To remain consistent with the terminology described above, when we say that a sequence $\{G_n\}$ of subgroups of ${\mathrm {SL}_2}(K)$ converges algebraically to G, we implicitly assume that there is an underlying group $\Gamma $ and surjective homomorphisms $\phi _n \colon \Gamma \to G_n$ . For each element $g \in G$ (where $g= \lim _{n \to \infty } \phi _n(\gamma )\in G$ for some $\gamma \in \Gamma $ ), we then use $g_n$ to denote the corresponding element $\phi _n(\gamma )$ of $G_n$ , so that $g= \lim _{n \to \infty } g_n$ for each $g \in G$ . In particular, by choosing $\Gamma $ to be the free group of rank r, this allows us to apply the notion of algebraic convergence to r-generator subgroups of ${\mathrm {SL}_2}(K)$ .

Theorem D. Let $\{G_n = \langle g_{1_n},\ldots ,g_{r_n}\rangle \}$ be a sequence of discrete nonelementary r-generator subgroups of ${\mathrm {SL}_2}(K)$ , where r is a positive integer. If $\{G_n\}$ converges algebraically to the group $G = \langle g_1,\ldots ,g_r \rangle \le {\mathrm {SL}_2}(K)$ , then G is discrete and nonelementary, and the maps $\psi _n:g_i\mapsto g_{i_n}$ extend to surjective homomorphisms ${\psi _n:G\to G_n}$ for sufficiently large n.

In Example 6.2, we show that Theorem D cannot be generalised to sequences of finitely generated subgroups of ${\mathrm {SL}_2}(K)$ that are not discrete, or that are discrete but elementary.

Theorem D implies the following nonarchimedean analogue of the main proposition in [14]. Since the Lie group ${\mathrm {SL}_2}(K)$ (where K is a p-adic field) is perfect and its Lie algebra is generated by two elements [19, Theorem 6], this is a very special case of a result by Breuillard and Gelander [4, Corollary 2.5].

Proposition 1.5. Let K be a p-adic field. Every dense subgroup of ${\mathrm {SL}_2}(K)$ contains two elements that generate a dense subgroup of ${\mathrm {SL}_2}(K)$ .

Remark 1.6. Throughout the paper, we often identify a subgroup G of ${\mathrm {SL}_2}(K)$ with its image $\overline {G}$ in $\mathrm {PSL_2}(K)$ , equipped with the quotient topology. By [18, Proposition 2.4], the topology on $\overline {G}$ is equivalent to the topology of pointwise convergence induced from the isometry group $\mathrm {Isom}(T_K)$ . The latter is equivalent to the compact-open topology; see Section 2.4, Theorem 1 and Section 3.4, Definition 1 in [3, Ch. X]. Note that G is discrete (respectively nonelementary) if and only if $\overline {G}$ is discrete (respectively nonelementary).

2 Proofs of Theorems A and B

We first establish the following criterion for discreteness (and its proof), which is a generalisation of [17, Lemma 4.4.1].

Lemma 2.1. Let G be a topological group that acts by isometries on a locally finite simplicial complex X. Suppose that G is equipped with the topology of pointwise convergence.

1. (1) If G is discrete, then $\mathrm {Stab}_G(y)$ is finite for every vertex $y\in X$ .

2. (2) If $\mathrm {Stab}_G(y)$ is finite for some vertex $y \in X$ , then G is discrete.

Proof. To prove the contrapositive of item (1), suppose that $H=\mathrm {Stab}_G(y)$ is infinite for some vertex y of X. Let $B_n$ be the ball of radius $n \in \mathbb {N}$ about y. Since X is locally finite, the following inductive argument shows that there are infinitely many distinct elements of H that fix each $B_n$ pointwise.

By the inductive hypothesis, we may assume that H has infinitely many elements that fix $B_n$ . Infinitely many of these elements, say $\{g_i : i\in I\}$ , induce the same permutation on the finitely many vertices in $B_{n+1}\setminus B_n$ . The set $\{g_ig_j^{-1} : i,j\in I\}$ then contains infinitely many distinct elements of H, each of which fixes $B_{n+1}$ pointwise. Hence, we may choose a sequence $\{g_n\}$ of distinct nontrivial elements of H such that $g_n$ fixes $B_n$ pointwise. Thus, $\{g_n\}$ converges to 1, so G is not discrete.

To prove item (2), suppose that $\mathrm {Stab}_G(y)$ is finite for some vertex y and suppose that $\{g_i\}$ is a sequence of elements of G converging to the identity. The sequence of vertices $\{g_i \cdot y \}$ converges to y, so there exists an N such that $g_i \in \mathrm {Stab}_G(y)$ for each $i\geq N$ . It follows that the sequence $\{g_i\}$ is eventually $1$ , and hence G is discrete.

We now prove a nonarchimedean version of [2, Theorem 4.3.5(i)].

Lemma 2.2. Let $A,B \in {\mathrm {SL}_2}(K)$ be such that $A \neq \pm 1$ . If A fixes at least one end of $T_K$ , then $\mathrm {tr}([A,B])=2$ if and only if A and B fix a common end of $T_K$ .

Proof. We first note that there is an ${\mathrm {SL}_2}(K)$ -equivariant isomorphism between the boundary $\partial T_K$ and the projective line $\mathbb {P}^1(K)$ [26]. Hence, after conjugation if necessary, we may assume that A fixes the end of $T_K$ corresponding to the eigenvector $(1,0)$ or, equivalently, A is upper triangular. A standard trace computation (similar to the proof of [2, Theorem 4.3.5(i)]) then shows that $\mathrm {tr}([A,B])=2$ if and only if either B is also upper triangular or A is diagonal and B is lower triangular. In either case, A and B fix a common end of $T_K$ .

Remark 2.3. If $A, B \in {\mathrm {SL}_2}(K)$ are such that $\mathrm {tr}([A,B])=2$ , then it is not necessarily the case that A and B must fix a common end of $T_K$ . Also, in contrast with the archimedean case [2, Theorem 4.3.5(i)], the fact that $A, B \in {\mathrm {SL}_2}(K)$ fix a common vertex of $T_K$ does not necessarily imply that $\mathrm {tr}([A,B])=2$ . See Example 6.3 for further details.

We also note the following results.

Proposition 2.4 [22, Proposition II.3.15].

The translation length of $X\in {\mathrm {SL}_2}(K)$ on $T_K$ is

$$ \begin{align*} l(X)=-2\ {\operatorname{min}}\{0,v(\mathrm{tr}(X))\}. \end{align*} $$

In particular, X is hyperbolic if and only if $v(\mathrm {tr}(X))<0$ .

Lemma 2.5. There are finitely many possible orders of finite order elements in ${\mathrm {SL}_2}(K)$ .

Proof. Let $q=p^r$ be the size of the residue field of K. If $X\in {\mathrm {SL}_2}(K)$ has finite order n coprime to p, then [9, Proposition 3.3] shows that $n \mid q \pm 1$ . If X has order $p^k$ , then X is unipotent and hence $k=1$ when $\mathrm {char}(K)>0$ by [20, page 964], and ${(p-1)p^{k-1}\le 2[K:\mathbb {Q}_p]}$ when $\mathrm {char}(K)=0$ by [25, Proposition 17, page 78] since either K or a quadratic extension of K must contain a $p^k$ th root of unity. Otherwise, if X has order $p^kn$ where $p\nmid n$ , then $X^{p^k}$ and $X^n$ have orders n and $p^k$ , respectively, so the result follows from the two cases above.

Since each finite order element of ${\mathrm {SL}_2}(K)$ has only finitely many possible traces, we obtain the following special case of [27, Lemma 2.4].

Corollary 2.6. The set $\{\mathrm {tr}(X) : X \in {\mathrm {SL}_2}(K)\ \mathrm{has\ finite\ order} \}$ is finite.

We now prove Theorems A and B. We first define the constant

$$ \begin{align*}M_K=\max\{v(\mathrm{tr}(X)-2) : X \in {\mathrm{SL}_2}(K) \text{ has finite order and } \mathrm{tr}(X) \neq 2\}.\end{align*} $$

Corollary 2.6 shows that $M_K$ is well defined. Moreover, since finite order elements of ${\mathrm {SL}_2}(K)$ are elliptic [26, I.4 Proposition 19], it follows from the ultrametric inequality and Proposition 2.4 that $M_K$ is nonnegative.

Proof of Theorem A.

Suppose that $G=\langle A,B \rangle \le {\mathrm {SL}_2}(K)$ is discrete and violates (1-1), that is,

$$ \begin{align*}{\operatorname{min}}\{v(\mathrm{tr}^2(A)-4), v(\mathrm{tr}([A,B])-2) \}> M_K\ge 0.\end{align*} $$

If A (respectively $[A,B]$ ) is hyperbolic, then [8, Ch. 2, Lemma 1.4] and Pro- position 2.4 imply that $v(\mathrm {tr}^2(A)-4)=v(\mathrm {tr}^2(A))<0$ (respectively $v(\mathrm {tr}([A,B])-2)= v(\mathrm {tr}([A,B]))<0$ ), which is a contradiction. Since G contains no infinite order elliptic elements by Lemma 2.1, we deduce that A and $[A,B]$ are both elliptic of finite order.

Now, after applying the well-known trace equality $\mathrm {tr}^2(A)=\mathrm {tr}(A^2)+2$ , it follows from the definition of $M_K$ that $\mathrm {tr}(A)=\pm 2$ and $\mathrm {tr}([A,B])=2$ . Hence, A has characteristic polynomial $x^2 \pm 2x +1=(x \pm 1)^2$ and repeated eigenvalue $\pm 1$ , so A fixes exactly one end $\eta $ of $T_K$ . Lemma 2.2 then shows that B fixes $\eta $ , thus G fixes an end of $T_K$ .

Proof of Theorem B.

Let $G=\langle A, B \rangle $ be a discrete nonelementary subgroup of ${\mathrm {SL}_2}(K)$ , where either $K=\mathbb {Q}_p$ or G contains no elements of order p. Since $v(2)$ and $v(4)$ are nonnegative, Proposition 2.4 and the ultrametric inequality show that (1-2) holds with strict inequality if A or $[A,B]$ is hyperbolic. Hence, we may assume that A and $[A,B]$ are elliptic.

If B is also elliptic, then the fixed point sets of A and B are disjoint since G is nonelementary. The proof of [10, 1.5] shows that the axes of $AB$ and $A^{-1}B^{-1}$ translate in the same direction along the unique geodesic between the fixed point sets of A and B. It follows from [10, 1.8] that $[A,B]$ is hyperbolic, which is a contradiction. Hence, B is hyperbolic.

Note that A and $BA^{-1}B^{-1}$ must fix a common vertex, as otherwise $[A,B]$ is hyperbolic by [10, 1.5]. Since A cannot fix an end of the translation axis $\mathrm {Ax}(B)$ of B, this implies that A fixes a subpath of $\mathrm {Ax}(B)$ of finite length $\Delta \ge l(B)$ .

Since G is discrete, A has finite order and $\Delta =l(B)$ by Lemma 2.1 and [9, Lemma 3.10]. Proposition 2.4 implies that $\Delta \ge 2$ and hence the fixed point set of A cannot be a vertex or an edge. Thus, A fixes two ends of $T_K$ by [9, Proposition 3.4] and is hence diagonalisable over K. Let $\lambda , \lambda ^{-1} \in K$ be the eigenvalues of A which, since G is nonelementary, must be distinct n th roots of unity for some $n>2$ . By Hensel’s lemma [25, II Section 4, Proposition 7], each n th root of unity in K is the unique lift of an n th root of unity modulo $\pi $ , where $\pi $ is the uniformiser of K. It follows that $\lambda \neq \lambda ^{-1} (\mod\pi) $ and hence ${v(\mathrm {tr}^2(A)-4)}=2v(\lambda -\lambda ^{-1})=0$ , so we obtain equality in (1-2).

3 Nonelementary groups

In the following two sections, we establish results that are necessary to prove the remaining statements in the introduction, some of which are interesting in their own right. Throughout, unless otherwise specified, we use T to denote a $\mathbb {R}$ -tree with path metric d, and $\mathrm {Isom}(T)$ to denote the isometry group of T. We equip $\mathrm {Isom}(T)$ with the topology of pointwise convergence.

As in [10], we consider each element $g \in \mathrm {Isom}(T)$ to be either elliptic or hyperbolic. We denote the corresponding translation length by $l(g)$ . We also denote the fixed point set of an elliptic isometry g by $\mathrm {Fix}(g)$ , and the translation axis of a hyperbolic isometry h by $\mathrm {Ax}(h)$ .

As in [12, Section 3.1], we say that a subgroup of $\mathrm {Isom}(T)$ of T is elementary if it stabilises a vertex, an end or a pair of ends of T, and nonelementary otherwise.

Lemma 3.1. If G is a nonelementary subgroup of $\mathrm {Isom}(T)$ , then it contains two hyperbolic elements whose axes have pairwise distinct ends.

Proof. We start by showing that G must contain a hyperbolic element g. Suppose for a contradiction that all elements of G are elliptic. Note that $\mathrm {Fix}(g_i)\cap \mathrm {Fix}(g_j) \neq \varnothing $ for each pair of distinct elements $g_i,g_j \in G$ , as otherwise, [10, 1.5] shows that $g_ig_j$ is hyperbolic. Hence, G fixes either a vertex or an end by [28, Lemma 1.6], which is a contradiction.

Let $\eta ^+,\eta ^-$ be the two ends of $\mathrm {Ax}(g)$ . We may suppose that the axis of every hyperbolic element of G has an end in common with $\mathrm {Ax}(g)$ , as otherwise, there is nothing to prove. Since G is nonelementary, there are hyperbolic elements $h_1, h_2$ such that $h_1$ fixes $\eta ^+$ (but not $\eta ^-$ ) and $h_2$ fixes $\eta ^-$ (but not $\eta ^+$ ). If $\mathrm {Ax}(h_1)$ and $\mathrm {Ax}(h_2)$ have pairwise distinct ends, then the proof is complete, so we may suppose that $\mathrm {Ax}(h_1)$ and $\mathrm {Ax}(h_2)$ have a common end $\zeta \notin \{\eta ^+, \eta ^-\}$ . Since the ends $\eta ^+$ and $\zeta $ of $\mathrm {Ax}(h_1)$ are distinct from the ends $h_2\cdot \eta ^+$ and $\eta ^-$ of $\mathrm {Ax}(h_2gh_2^{-1})=h_2\cdot \mathrm {Ax}(g)$ , this proves the lemma.

We now observe that in a discrete group G of isometries of a locally finite simplicial tree T, no element of G can fix precisely one end of the axis of a hyperbolic element of G.

Lemma 3.2. Let G be a discrete subgroup of $\mathrm {Isom}(T)$ , where T is a locally finite simplicial tree. Suppose that $h\in G$ is hyperbolic. If $g\in G$ fixes at least one end of $\mathrm {Ax}(h)$ , then g commutes with a power of h, whence g fixes both ends of $\mathrm {Ax}(h)$ .

Proof. Let $\eta ^-$ and $\eta ^+$ , respectively, be the repelling and attracting ends of $\mathrm {Ax}(h)$ . Without loss of generality, we may suppose that g fixes $\eta ^-$ .

If g is elliptic, then g fixes a halfray R on $\mathrm {Ax}(h)$ . If x is a point on R, then $h^igh^{-i}$ fixes x for each $i\geq 0$ . Since $\mathrm {Stab}_G(x)$ is finite by Lemma 2.1, we obtain that $h^igh^{-i}=h^jgh^{-j}$ for some distinct i and j. Thus, g commutes with $h^k$ , where $k=i-j$ .

If g is hyperbolic, then $\mathrm {Ax}(g)$ intersects $\mathrm {Ax}(h)$ in at least a halfray R and we may assume (by inverting g if necessary) that $\eta ^-$ is also the repelling end of $\mathrm {Ax}(g)$ . Let $x \in R$ and observe that $gh^ig^{-1}h^{-i}$ fixes x for each $i\geq 0$ . A similar argument to above then shows that g commutes with $h^k$ for some integer k.

In either case, $g \cdot \eta ^+ = gh^k \cdot \eta ^+ = h^k (g \cdot \eta ^+)$ , so $g \cdot \eta ^+ \in \{\eta ^-,\eta ^+\}$ . Hence, g fixes $\eta ^+$ .

We also prove the following nonarchimedean analogue of [16, Lemma 5].

Lemma 3.3. Suppose that $G = \langle g_1,\ldots ,g_r \rangle \le \mathrm {Isom}(T)$ is a discrete nonelementary subgroup of $\mathrm {Isom}(T)$ , where T is a locally finite simplicial tree. If $h \in G$ has infinite order, then the group $\langle g_i,h \rangle $ is nonelementary for some $i\in \{1,\ldots ,r\}$ .

Proof. By Lemma 2.1, h must be hyperbolic. Let $\eta ^-$ and $\eta ^+$ be the ends of $\mathrm {Ax}(h)$ and suppose for a contradiction that $\langle g_i,h \rangle $ is elementary for every i. By Lemma 3.2, $g_i$ cannot fix precisely one of $\eta ^-$ or $\eta ^+$ , and hence $g_i$ stabilises the set $\{\eta ^-,\eta ^+\}$ . Thus, G stabilises $\{\eta ^-,\eta ^+\}$ and is hence elementary, which is a contradiction.

We recall the following well-known nonarchimedean analogue of Scott’s core theorem [24].

Lemma 3.4. A discrete, nonelementary and compactly generated subgroup G of ${\mathrm {SL}_2}(K)$ is finitely presented.

Proof. Since G is a discrete subgroup of a Hausdorff group, it is closed. Hence, by [7, Remark 2.3 and Lemma 2.4], there exists a subtree of T on which the action of G is cocompact. Since G acts properly on $T_K$ , it follows from [5, Corollary I.8.11] that G is finitely presented.

Finally, we show that within the class of discrete subgroups of ${\mathrm {SL}_2}(K)$ , the property of being nonelementary is preserved under isomorphism. In general, this property does not have to be preserved under isomorphism; see Example 6.4.

Lemma 3.5. A discrete subgroup G of ${\mathrm {SL}_2}(K)$ is elementary if and only if it is virtually abelian. In particular, if $G_1$ and $G_2$ are isomorphic discrete subgroups of ${\mathrm {SL}_2}(K)$ , then $G_1$ is nonelementary if and only if $G_2$ is nonelementary.

Proof. Let G be a discrete elementary subgroup of ${\mathrm {SL}_2}(K)$ . If G fixes a vertex of $T_K$ , then G is finite by Lemma 2.1. So suppose that G fixes precisely one end of $T_K$ . By Lemma 3.2, G consists entirely of finite order elliptic elements. Using the identification of $\partial T_K$ with the projective line $\mathbb {P}^1(K)$ [26, page 72], we may conjugate G into a group of upper triangular matrices. Its unipotent elements form an abelian normal subgroup H of G, such that $G/H$ can be identified with a finite subgroup of the collection of roots of unity of K; for instance, see the argument given in [2, page 87]. (Note that, in this case, H is trivial if $\mathrm {char}(K)=0$ , and is an elementary abelian p-group if $\mathrm {char}(K)=p>0$ .) Hence, G is virtually abelian. Finally, we suppose that G stabilises a pair of ends of $T_K$ . Thus, G contains a subgroup H of index at most two which pointwise fixes these two ends. Again using the identification of $\partial T_K$ with $\mathbb {P}^1(K)$ , we may assume by conjugation that H consists entirely of diagonal matrices and is therefore abelian.

Conversely, suppose that G is discrete and virtually abelian. If G is finite, then it fixes a vertex of $T_K$ by [28, 2.3.1], so suppose that G is infinite. In particular, G contains an infinite abelian normal subgroup H. If H contains a hyperbolic element h, then Lemmas 2.2 and 3.2 show that every element of H fixes both ends $\eta ^\pm $ of $\mathrm {Ax}(h)$ . Moreover, if $g\in G\setminus H$ , then since $H\trianglelefteq G$ , we obtain that $(g^{-1}Hg)(\eta ^{\pm }) = \eta ^{\pm }$ , whence g stabilises $\{\eta ^+, \eta ^-\}$ . However, if H contains only elliptic elements, then [28, Lemma 1.6] implies that H fixes either a vertex or an end of $T_K$ . The former option contradicts Lemma 2.1, whence H fixes an end of $T_K$ and a similar argument to the above then shows that G fixes this same end.

4 Converging sequences

Using the same notation as in the previous section, we continue to establish some results needed to prove the remaining statements in the introduction.

Lemma 4.1. Let $\{g_n\}$ be a sequence of elements of $\mathrm {Isom}(T)$ converging to $g \in \mathrm {Isom}(T)$ .

1. (1) If g is elliptic and there is a uniform lower bound $l_{\operatorname {min}}$ on the translation length of hyperbolic elements in the sequence $\{g_n\}$ , then the sequence $\{g_n\}$ is eventually elliptic.

2. (2) If g is hyperbolic, then the sequence $\{g_n\}$ is eventually hyperbolic.

Proof. If g is elliptic, then let $x \in \mathrm {Fix}(g)$ . Using the topology of pointwise convergence, we may choose a positive integer N such that $d(g_n\cdot x, x)=d(g_n\cdot x, g \cdot x)<l_{\operatorname {min}}$ for each $n \ge N$ . It follows that $g_n$ fixes x for each $n \ge N$ .

However, if g is hyperbolic, then assume for a contradiction that there is a subsequence $\{h_n\}$ of $\{g_n\}$ that consists only of elliptic elements and converges to g. Let x be a point of T and let m be the midpoint of $[x, g\cdot x]$ . Using the topology of pointwise convergence, we may choose a positive integer N such that $d(h_n\cdot x,g \cdot x)<\tfrac 12l(g)$ and $d(h_n \cdot m, g \cdot m)<\tfrac 12l(g)$ for each $n \ge N$ . By [10, 1.3(iii)], the midpoint $m_n$ of $[x, h_n\cdot x]$ is fixed by $h_n$ for every n. Note that $d(m_n,m)\leq \tfrac 12 d(h_n \cdot x, g\cdot x)<\tfrac 14l(g)$ by [5, Proposition II.2.2] and thus

$$ \begin{align*}d(h_n\cdot m,m)\leq d(h_n\cdot m,h_n\cdot m_n)+d(h_n \cdot m_n,m_n)+d(m_n,m)<\tfrac{1}{2}l(g)\end{align*} $$

for each $n \ge N$ . Hence, $d(g\cdot m,m)\leq d(g\cdot m,h_n\cdot m)+d(h_n\cdot m,m)<l(g)$ for sufficiently large n, which is a contradiction.

Remark 4.2. Without the bound $l_{\operatorname {min}}$ in Lemma 4.1(1), one could take a sequence of hyperbolic elements $\{g_n\}$ of translation length ${1}/{n}$ that converges to an elliptic element of $\mathrm {Isom}(T)$ .

We obtain the following nonarchimedean analogue of [13, Lemma 2] as a consequence of Lemma 4.1(1). Note that this version does not use Theorem A; this contrasts with the proof in [13] which requires Jørgensen’s inequality.

Corollary 4.3. Let $\{g_n\}$ be a sequence of elements of ${\mathrm {SL}_2}(K)$ such that the cyclic groups $\langle g_n \rangle $ are discrete. If $\{g_n\}$ converges to an elliptic element $g \in {\mathrm {SL}_2}(K)$ , then the sequence $\{\mathrm {tr}(g_n)\}$ is eventually constant.

Proof. By Lemma 4.1(1), the sequence $\{g_n\}$ is eventually elliptic. It follows from Lemma 2.1 that $\{g_n\}$ eventually consists of finite order elements. Since the trace function is continuous, Corollary 2.6 shows that $\{\mathrm {tr}(g_n)\}$ is eventually constant.

Lemma 4.4. Let $\{G_n\}$ be a sequence of elementary subgroups of $\mathrm {Isom}(T)$ . If $\{G_n\}$ converges algebraically to G, then G is elementary.

Proof. Suppose for a contradiction that G is nonelementary. By Lemma 3.1, there are hyperbolic elements $h_1, h_2 \in G$ such that the ends of $\mathrm {Ax}(h_1)$ and $\mathrm {Ax}(h_2)$ are distinct. Without loss of generality, we may assume that $h_1$ and $h_2$ translate in the same direction along the (possibly empty) finite path $\mathrm {Ax}(h_1) \cap \mathrm {Ax}(h_2)$ . There is some positive integer k such that $\mathrm {Ax}(h_1)$ and $\mathrm {Ax}(h_2^kh_1^{-1}h_2^{-k})=h_2^k\cdot \mathrm {Ax}(h_1)$ intersect along a (possibly empty) path of length strictly less than $l(h_1)$ , and hence [10, 1.5 and 3.4] show that $[h_1,h_2^k]$ is hyperbolic. By Lemma 4.1(2), there is a sufficiently large positive integer N such that the corresponding elements $h_{1_N}$ , $h_{2_N}$ and $[h_{1_N},h_{2_N}^k]$ of $G_N$ are hyperbolic. Since $[h_{1_N},h_{2_N}^k]$ is hyperbolic, $\mathrm {Ax}(h_{1_N})$ and $\mathrm {Ax}(h_{2_N})$ must have finite (or empty) overlap by [10, Corollary 2.3], which contradicts the fact that $G_N$ is elementary.

The following is a nonarchimedean analogue of [16, Lemma 9]. Note that the assumption of eventual discreteness is necessary; see Example 6.5.

Lemma 4.5. Let $\{G_n=\langle g_n, h_n \rangle \}$ be a sequence of subgroups of ${\mathrm {SL}_2}(K)$ converging algebraically to $G = \langle g,h \rangle \le {\mathrm {SL}_2}(K)$ , where h is hyperbolic. If $\{G_n\}$ is eventually discrete, then g fixes an end of $\mathrm {Ax}(h)$ if and only if $g_n$ and $h_n$ fix a common end of $T_K$ for all sufficiently large n.

Proof. Suppose first that $g_n$ and $h_n$ fix a common end of $T_K$ for all sufficiently large n. By Lemma 2.2, $\mathrm {tr}([g_n,h_n])=2$ for all sufficiently large n, and so $\mathrm {tr}([g,h])=2$ since the trace function is continuous. Hence, Lemma 2.2 shows that g fixes an end of $\mathrm {Ax}(h)$ .

Conversely, suppose that g fixes an end of $\mathrm {Ax}(h)$ . By Lemma 2.2, $\mathrm {tr}([g,h])=2$ and hence $[g,h]$ is elliptic by Proposition 2.4. Corollary 4.3 then shows that $\mathrm {tr}([g_n,h_n])=2$ for all sufficiently large n. Since $h_n$ is hyperbolic for sufficiently large n by Lemma 4.1 $(2)$ , another application of Lemma 2.2 proves the result.

We use the following technical lemma several times.

Lemma 4.6. Let $g \in {\mathrm {SL}_2}(K)$ and suppose that $h_1, h_2 \in {\mathrm {SL}_2}(K)$ are hyperbolic elements whose axes have pairwise distinct ends. If both $\langle g,h_1 \rangle $ and $ \langle g,h_2 \rangle $ are elementary groups, then $g=\pm 1$ .

Proof. Since $\langle g,h_1 \rangle $ and $\langle g,h_2 \rangle $ are elementary, g stabilises the ends of both $\mathrm {Ax}(h_1)$ and $\mathrm {Ax}(h_2)$ . Hence, $g^2$ fixes four ends of $T_K$ and, since $\partial T_K$ can be identified with the projective line $\mathbb {P}^1(K)$ [26, page 72], it follows that $g^2=1$ .

We conclude this section by proving a nonarchimedean analogue of [13, Proposition 1].

Proposition 4.7. Let G be a nonelementary subgroup of ${\mathrm {SL}_2}(K)$ and let $\{G_n\}$ be a sequence of eventually discrete subgroups of ${\mathrm {SL}_2}(K)$ . If $\{G_n\}$ converges algebraically to G, then G is discrete.

Proof. Let $\{g_i\}$ be a sequence of elements of G converging to $1$ . By Lemma 3.1, we may choose hyperbolic elements $h_1, h_2 \in G$ whose axes have no end in common. Observe that the sequences $\{[g_i,h_1]\}$ and $\{[g_i,h_2]\}$ both converge to $1$ . For sufficiently large i and n, it follows that ${\operatorname {min}}\{v(\mathrm {tr}^2(g_{i_n})-4), v(\mathrm {tr}([g_{i_n},h_{j_n}])-2)\}>M_K$ for $j \in \{1,2\}$ . Theorem A hence implies that the subgroups $\langle g_{i_n}, h_{1_n} \rangle $ and $\langle g_{i_n}, h_{2_n}\rangle $ of $G_n$ are elementary for sufficiently large i and n. By Lemma 4.4, the subgroups $\langle g_i, h_1 \rangle $ and $\langle g_i, h_2 \rangle $ of G are also elementary for sufficiently large i. Hence, $\{g_i\}$ is eventually constant by Lemma 4.6, so G is discrete.

5 Proofs of the remaining statements

Proof of Proposition 1.2.

Let G be a nonelementary subgroup of ${\mathrm {SL}_2}(K)$ . If G is discrete, then so is every subgroup of G. So suppose that every two-generator subgroup of G is discrete, and that $\{g_i\}$ is a sequence of elements of G converging to $1$ . By Lemma 3.1, we may choose hyperbolic elements $h_1, h_2 \in G$ whose axes have pairwise distinct ends. For sufficiently large i, the following inequality holds for each $j \in \{1,2\}$ :

$$ \begin{align*} {\operatorname{min}}\{v(\mathrm{tr}^2(g_i)-4), v(\mathrm{tr}([g_i,h_j]-2)\}>M_K.\end{align*} $$

Hence, Theorem A shows that $\langle g_i, h_1\rangle $ and $\langle g_i, h_2\rangle $ are both elementary for sufficiently large i. By Lemma 4.6, $\{g_i\}$ is eventually constant and hence G is discrete.

Proof of Proposition 1.3.

If G is discrete, then every cyclic subgroup of G is discrete. Hence, we may suppose that every cyclic subgroup of G is discrete. Since G acts by isometries on a locally finite simplicial building X of type $\tilde {A}_{n-1}$ [6, 2.2.8 and 7.4.11], Lemma 2.1 shows that every element in G that fixes a vertex of X has finite order. Thus, every vertex stabiliser in G is periodic, that is, it consists only of finite order elements. Moreover, every vertex stabiliser in G has finite exponent by Lemma 2.5. Thus, every vertex stabiliser in G is finite by [29, Theorem 9.1(ii) and (iii)], so G is discrete by Lemma 2.1.

Proof of Theorem C.

We first prove that $\phi $ is an isomorphism. Since $\phi $ is surjective by construction, it suffices to show that $\phi $ is injective.

Let $A \in \Gamma $ be nontrivial. If A is hyperbolic, then the proof of Lemma 3.1 shows that we may choose a hyperbolic element $B \in \Gamma $ such that $\mathrm {Ax}(A)$ and $\mathrm {Ax}(B)$ have pairwise distinct ends. If A is elliptic, then there exists a hyperbolic element $B \in \Gamma $ such that A does not stabilise the set of ends of $\mathrm {Ax}(B)$ . In either case, there exists a hyperbolic element $B \in \Gamma $ such that $\langle A, B \rangle $ is nonelementary. By Lemma 3.5, $\langle \phi _n(A), \phi _n(B) \rangle $ is then a nonelementary subgroup of $G_n$ for sufficiently large n.

Now suppose for a contradiction that $\phi (A)=1$ . The sequence $\{\phi _n(A)\}$ converges to $1$ , so for sufficiently large n, we obtain

$$ \begin{align*}{\operatorname{min}}\{v(\mathrm{tr}^2(\phi_n(A))-4),v(\mathrm{tr}([\phi_n(A),\phi_n(B)])-2)\}>M_K.\end{align*} $$

Theorem A then implies that $\langle \phi _n(A), \phi _n(B) \rangle $ is elementary for sufficiently large n, which gives the desired contradiction. Hence, $\phi $ is an isomorphism.

Now suppose that $\{g_i=\phi (\gamma _i)\}$ is a sequence of elements of G converging to $1$ . Since $G_n$ is isomorphic to $\Gamma $ , Lemma 3.5 shows that $G_n$ is nonelementary for sufficiently large n. For each such n, there exist hyperbolic elements $\phi _n(h_1), \phi _n(h_2) \in G_n$ whose axes have pairwise distinct ends by Lemma 3.1. For sufficiently large i and n, observe that

$$ \begin{align*}{\operatorname{min}}\{v(\mathrm{tr}^2(\phi_n(\gamma_i)-4)), v(\mathrm{tr}([\phi_n(\gamma_i),\phi_n(h_j)])-2)\}>M_K\end{align*} $$

for $j \in \{1,2\}$ . Theorem A hence implies that the subgroups $\langle \phi _n(\gamma _i), \phi _n(h_1) \rangle $ and $\langle \phi _n(\gamma _i), \phi _n(h_2)\rangle $ of $G_n$ are elementary for sufficiently large i and n. Lemma 4.6 thus shows that $\phi _n(\gamma _i)=\pm 1$ for sufficiently large i and n. Since $\phi _n$ and $\phi $ are isomorphisms, it follows that $\{g_i=\phi (\gamma _i)\}$ is eventually 1, whence G is discrete. Moreover, Lemma 3.5 shows that G is nonelementary.

Proof of Theorem D.

By Proposition 4.7, if G is nonelementary, it is also discrete, so we start by proving the former.

For each n, one of the elements in the set ${\{g_{i_n} : 1 \leq i \leq n\} \cup \{ g_{i_n}g_{j_n} : 1\leq i<j \leq r\}}$ must be hyperbolic as otherwise, $G_n$ fixes a point [26, I.6.5 Corollary 2 of Proposition 26] and is hence elementary. We denote this hyperbolic element by $h_n$ . By Lemma 3.3, for each n, there exists $i_n \in \{1,\ldots , r\}$ such that the group $H_n = \langle h_n, g_{i_n} \rangle $ is discrete and nonelementary. Since each $G_n$ is finitely generated, for infinitely many n, we must have picked the same indices to define both generators of $H_n$ . Hence, there exists a subsequence of $\{H_n\}$ converging to some two-generator subgroup H of G. Since G is nonelementary when H is, it thus suffices to prove the statement for $r=2$ .

If every element of $\{g_1, g_2, g_1g_2\}$ is elliptic, then Lemma 4.1(1) shows that every element of $\{g_{1_n}, g_{2_n}, g_{1_n}g_{2_n}\}$ is also elliptic for sufficiently large n. By [26, I.6.5 Corollary 2 of Proposition 26], $G_n$ is elementary, which is a contradiction. Hence, we may choose some hyperbolic element $h \in \{g_1, g_2, g_1g_2\}$ .

If $g \in \{g_1, g_2, g_1g_2\} \backslash \{h\}$ is such that $ghg^{-1}$ fixes an end of $\mathrm {Ax}(h)$ , then Lemmas 4.1(2) and 4.5 show that, for n sufficiently large, $h_n$ is hyperbolic and $g_nh_ng_n^{-1}$ fixes an end of $\mathrm {Ax}(h_n)$ . Thus, Lemma 3.2 shows that $G_n$ is elementary, which is a contradiction. Therefore, there is some $g \in \{g_1, g_2, g_1g_2\}\backslash \{h\}$ such that the hyperbolic elements h and $ghg^{-1}$ have no ends in common, so G is nonelementary (and hence discrete).

To prove that the maps $\psi _n:g_i\mapsto g_{i_n}$ extend to surjective homomorphisms, we argue as in [13, Theorem 2]. Note that Lemma 3.4 shows that G is finitely presented. Therefore, a necessary and sufficient condition for $\psi _n$ to be a homomorphism is that the images of relators in G are equal to the identity.

Let $R_1,\ldots ,R_k$ be a basis for the relations for G. It remains to find a sufficiently large N such that for $n\geq N$ , the corresponding elements in $G_n$ are equal to the identity. By Lemma 3.1, we can find two hyperbolic elements $h_1, h_2 \in G$ whose axes have pairwise distinct ends. It follows from Lemmas 4.1(2) and 4.5 that, for sufficiently large n, there exist hyperbolic elements $h_{1_n}, h_{2_n} \in G_n$ whose axes have pairwise distinct ends.

Since the sequence $\{G_n\}$ converges to G, the corresponding elements $R_{s_n}$ converge to $1$ for each $s\in \{1,\ldots ,k\}$ . By Theorem A, the groups $\langle R_{s_n}, h_{t_n} \rangle $ are elementary for each $s\in \{1,\ldots ,k\}$ , $t\in \{1,2\}$ and sufficiently large n. Hence, Lemma 4.6 shows that $R_{s_n}=1$ for each $s\in \{1,\ldots ,k\}$ and sufficiently large n.

Proof of Proposition 1.5.

Let G be dense in ${\mathrm {SL}_2}(K)$ . Since ${\mathrm {SL}_2}(K)$ contains a two-generator dense subgroup, there exist $g,h\in \overline {G}$ that generate a dense subgroup H of ${\mathrm {SL}_2}(K)$ . Let $\{g_n\}$ and $\{h_n\}$ be sequences of elements of G converging to g and h, respectively. If all but finitely many of the subgroups $H_n =\langle g_n, h_n \rangle $ of G are elementary, then H is elementary by Lemma 4.4. This is a contradiction by [9, Lemma 6.6], so we may assume without loss of generality that the sequence $\{H_n\}$ consists entirely of nonelementary subgroups of G. If all but finitely many of these subgroups are discrete, then H is discrete by Theorem D, which is again a contradiction. Hence, there exists a positive integer N such that $H_N$ is nonelementary and not discrete. It follows from [9, Lemmas 6.6 and 6.7] that $H_N$ is dense.

6 Examples

In this final section, we include several examples which are referred to throughout the paper.

Example 6.1. Let p be a prime and let G be the subgroup of ${\mathrm {SL}_2}(\mathbb {F}_p((t)))$ generated by

$$ \begin{align*}X=\left\lbrace \left[ \begin{array}{@{}cc@{}} 1 & x \\ 0 & 1 \end{array} \right] : x \in \mathbb{F}_p[[t]] \right\rbrace.\end{align*} $$

Each element of X has order p and fixes the vertex corresponding to $\mathbb {F}_p[[t]]^2$ in the corresponding Bruhat–Tits tree. Since X is infinite, G is not discrete by Lemma 2.1. However, every two elements of X generate a finite (and hence discrete) group.

Example 6.2. We define the following matrices in ${\mathrm {SL}_2}(\mathbb {Q}_p)$ :

$$ \begin{align*}A_n=\left[ \begin{array}{@{}cc@{}} 1 & p^n \\ 0 & 1 \end{array} \right], \quad B=\left[ \begin{array}{@{}cc@{}} p & 0 \\ 1 & \dfrac{1}{p} \end{array} \right], \quad C=\left[ \begin{array}{@{}cc@{}} p & 0 \\ 0 & \dfrac{1}{p} \end{array} \right], \quad D_n=\left[ \begin{array}{@{}cc@{}} 1+p^n & 1 \\ 0 & \dfrac{1}{1+p^n} \end{array} \right].\end{align*} $$

Observe that:

• • each group $G_n=\langle A_n, B \rangle $ is nonelementary and not discrete, but $\{G_n\}$ converges algebraically to the elementary discrete group $\langle B \rangle \cong \mathbb {Z}$ ;

• • each group $H_n=\langle A_n, C \rangle $ is elementary and not discrete, but $\{H_n\}$ converges algebraically to the elementary discrete group $\langle C \rangle \cong \mathbb {Z}$ ;

• • each group $\langle D_n \rangle $ is elementary and discrete, but $\{ \langle D_n \rangle \}$ converges algebraically to an elementary group that is not discrete.

Example 6.3. Note that $-3$ is a quadratic residue modulo $7$ , so Hensel’s lemma shows that we can define the following matrices of ${\mathrm {SL}_2}(\mathbb {Q}_{7})$ which commute:

$$ \begin{align*}A=\left[ \begin{array}{@{}cc@{}} 0 & -1 \\ 1 & 0 \end{array} \right], \quad B=\left[ \begin{array}{@{}cc@{}} 2 & -\sqrt{-3} \\ \sqrt{-3} & 2 \end{array} \right].\end{align*} $$

Since $\mathrm {tr}^2(A)-4=-4$ and $\mathrm {tr}^2(B)-4=12$ are both quadratic nonresidues modulo $7$ , the matrices A and B are not diagonalisable over $\mathbb {Q}_{7}$ and therefore fix no ends of $T_{\mathbb {Q}_7}$ .

However, A and B are elements of ${\mathrm {SL}_2}(\mathbb {Z}_{7})$ and hence they both fix the vertex of $T_{\mathbb {Q}_7}$ corresponding to $\mathbb {Z}_{7}^2$ . In general, however, two elements of ${\mathrm {SL}_2}(K)$ that fix a common vertex need not have the trace of their commutator equal to 2; for instance, consider the pair of generators for ${\mathrm {SL}_2}(\mathbb {Z})$ in Example 6.4.

Example 6.4. Let ${\mathrm {SL}_2}(\mathbb {Z})\cong C_4 *_{C_2} C_6$ be the group generated by the matrices

$$ \begin{align*}\left[ \begin{array}{@{}cc@{}} 0 & -1 \\ 1 & 0 \end{array} \right] \quad\text{and}\quad \left[ \begin{array}{@{}cc@{}} 0 & -1 \\ 1 & 1 \end{array} \right];\end{align*} $$

see [26, Ch. I, 1.5.3]. Since ${\mathrm {SL}_2}(\mathbb {Z})$ fixes the vertex of $T_{\mathbb {Q}_p}$ corresponding to $\mathbb {Z}_p^2$ and also contains infinite order elliptic elements, it is an elementary nondiscrete subgroup of ${\mathrm {SL}_2}(\mathbb {Q}_p)$ . However, the subgroup of ${\mathrm {SL}_2}(\mathbb {Q}_p)$ generated by the matrices

$$ \begin{align*}\left[ \begin{array}{@{}cc@{}} 0 & -1 \\ 1 & 0 \end{array} \right] \quad\text{and}\quad \left[ \begin{array}{@{}cc@{}} 0 & -\dfrac{1}{p} \\ p & 1 \end{array} \right]\end{align*} $$

is discrete, nonelementary and also isomorphic to $C_4 *_{C_2} C_6$ ; for the corresponding quotient in $\mathrm {PSL_2}(K)$ , see [9, Section 5, Case $\left(\mathrm{c}\right)$ ].

Example 6.5. We define the following matrices in ${\mathrm {SL}_2}(\mathbb {Q}_p)$ :

$$ \begin{align*} A_n=\left[ \begin{array}{@{}cc@{}} 1+p^n & 1 \\ p^n & 1 \end{array} \right], \quad A=\left[ \begin{array}{@{}cc@{}} 1 & 1 \\ 0 & 1 \end{array} \right], \quad B=\left[ \begin{array}{@{}cc@{}} p & 0 \\ 0 & \dfrac{1}{p} \end{array} \right].\end{align*} $$

The sequence of nondiscrete groups $\{\langle A_n,B\rangle \}$ converges algebraically to $\langle A,B \rangle $ . Each elliptic element $A_n$ does not fix an end of $\mathrm {Ax}(B)$ , whereas A does fix an end of $\mathrm {Ax}(B)$ .