This paper reviews various symbolisms for the two-valued propositional calculus, and introduces a new set of signs which embodies the principles of Leśniewski's symbolism, yet resembles better known signs. This type of symbolism, serving as a diagram, may be used either in place of or as auxiliary to the usual symbolisms.

This paper will be concerned with an adaptation of Parry's trapezoid symbolism to the solving of problems.

In Parry's notation ‘pq’, in particular, sets forth the relationship that obtains when p is true, whether q be true or false. The symbol may also be regarded as manifesting the matrix analysis of p. It is this aspect which offers promise for manipulation. We propose to write the symbol ‘’ for p itself. It is to be kept in mind, however, that ‘’ is the symbol of p when there are but two variables. How to proceed when there are more than two will be seen later.

The symbol for q will in like manner be ‘⌋’.

Let ‘’ and ‘’, then, be regarded as elemental symbols setting forth the matrix analysis of the variables. Suppose further that in transcribing from conventional to the trapezoid symbolism we substitute for the variables only, retaining the constants (antithetically to Parry's procedure). Thus ‘p ∨ q’ becomes, not ‘pq’ as with Parry, but ‘ ∨ ’. Problem-solving consists of merging the trapezoidal symbols according to procedures specified by the constants. As symbols are merged, the constants are eliminated.

The resultant symbol constitutes the solution.

The rules for merging symbols are derived from the elementary processes of forming truth-tables:

Disjunction of two symbols consists of superimposing them.

Conjunction consists of preserving only such sides as are common to both the conjoined symbols.

In a previous paper I have described a decision method for testing whether or not two arbitrary finite truth-tables are “equal”, i.e., determine the same set of tautologies. The same problem for the case of infinite truth-tables remained open.

In the present note we shall show that the answer to the problem in the case of infinite truth-tables is negative; in fact we shall prove that there exists neither a decision method for testing the equality of arbitrary truth-tables, nor even one for testing the equality of what we call “recursive” truth-tables.

The terminology of Kalicki [3] will be used; for brevity's sake the discussion involving the notions of recursiveness and recursive enumerability uses the informal terminology and mode of argumentation employed by Post in [9].

Quantification theory, or the first-order predicate calculus, is ordinarily so formulated as to provide as theorems all and only those formulas which come out true under all interpretations in all non-empty domains. There are two strong reasons for thus leaving aside the empty domain.

(i) Where D is any non-empty domain, any quantificational formula which comes out true under all interpretations in all domains larger than D will come out true also under all interpretations in D. (Cf. [4], p. 92.) Thus, though any small domain has a certain triviality, all but one of them, the empty domain, can be included without cost. To include the empty one, on the other hand, would mean surrendering some formulas which are valid everywhere else and thus generally useful.

(ii) An easy supplementary test enables us anyway, when we please, to decide whether a formula holds for the empty domain. We have only to mark the universal quantifications as true and the existential ones as false, and apply truth-table considerations.

Incidentally, the existence of that supplementary test shows that there is no difficulty in framing an inclusive quantification theory (i.e., inclusive of the empty domain) if we so desire. A proof in this theory can be made to consist simply of a proof in the exclusive (or usual) theory followed by a check by the method of (ii). We may, however, be curious to see a more direct or autonomous formulation: one which does not consist, like the above, of the exclusive theory plus a rule of expurgation. And, in fact, such formulations have of late been forthcoming: Mostowski [5], Hailperin [3], and, as part of a broader context, Church [2]. I shall not presuppose acquaintance with these papers, except in my final paragraph (and then only with [3]).

Consider any interpreted theory Θ, formulated in the notation of quantification theory (or lower predicate calculus) with interpreted predicate letters. It will be proved that Θ is translatable into a theory, likewise formulated in the notation of quantification theory, in which there is only one predicate letter, and it a dyadic one.

Let us assume a fragment of set theory, adequate to assure the existence, for all x and y without regard to logical type, of the set {x, y) whose members are x and y, and to assure the distinctness of x from {x, y} and {{x}}. ({x} is explained as {x, x}.) Let us construe the ordered pair x; y in Kuratowski's fashion, viz. as {{x}, {x, y}}, and then construe x;y;z as x;(y;z), and x;y;z;w as x;(y;z;w), and so on. Let us refer to w, w;w, w;w;w, etc. as 1w, 2w, 3w, etc.

Suppose the predicates of Θ are ‘F1’, ‘F2’, …, finite or infinite in number, and respectively d1-adic, d2-adic, …. Now let Θ′ be a theory whose notation consists of that of quantification theory with just the single dyadic predicate ‘F’, interpreted thus:

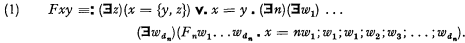
The universe of Θ′ is to comprise all objects of the universe of Θ and, in addition, {x, y) for every x and y in the universe of Θ′. (Of course the universe of Θ may happen already to comprise all this.)

Now I shall show how the familiar notations ‘x = y’, ‘x = {y, z}’, etc., and ultimately the desired ‘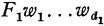’, ‘’, 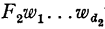etc. themselves can all be defined within Θ′.

In this paper we consider certain formal properties of deductive systems which, in special cases, reduce to the property of ω-consistency; and we then seek to understand the significance of these properties by relating them to the use of models in providing interpretations of the deductive systems.

The notion of ω-consistency arises in connection with deductive systems of arithmetic. For definiteness, let us suppose that the system is a functional calculus whose domain of individuals is construed as the set of natural numbers, and that the system possesses individual constants ν0, ν1, ν2, … such that νi functions as a name for the number i. Such a system is called ω-consistent, if there is no well-formed formula A(x) (in which x is the only free variable) such that A(ν0), A(ν1), A(ν2), … and ∼(x)A(x) are all formal theorems of the system, where A(νi) is the formula resulting from A(x) by substituting the constant νi for each free occurrence of the individual variable x.

Now consider an arbitrary applied functional calculus F, and let Γ be any non-empty set of its individual constants. In imitation of the definition of ω-consistency, we may say that the system F is Γ-consistent, if it contains no formula A(x) (in which x is the only free variable) such that ⊦ A (α) for every constant α in Γ, and also ⊦ ∼(x)A(x) (where an occurrence of “⊦” indicates that the formula which it precedes is a formal theorem). We easily see that the condition of Γ-consistency is equivalent to the condition that the system F contain no formula B(x) such that ⊦ ∼ B(α) for each α in Γ, and also ⊦ (∃x)B(x).

1. In this paper we construct a model for part of the system NF of [4]. Specifically, we define a relation R of natural numbers such that the R-relativiseds of all the axioms except P9 of Hailperin's finitization [2] of NF become theorems of say Zermelo set theory. We start with an informal explanation of the model.

2. Scrutiny of P1-P8 of [2] suggests that a model for these axioms might be constructed by so to speak starting with a universe that contained a “universe set” and a “cardinal 1”, and passing to its closure under the operations implicit in P1-P7, viz., the Boolean, the domain, the direct product, the converse, and the mixtures of product and inverse operations represented by P3 and P4. To obtain such closure we must find a way of representing the operations that involve ordered pairs and triples.

We take as universe of the model the set of natural numbers ω; we let 0 represent the “universe set” and 1 represent “cardinal 1”. Then, in order to be able to refer in the model to the unordered pair of two sets, we determine all representatives of unordered pairs in advance by assigning them the even numbers in unique fashion (see d3 and d25); we can now define the operations that involve ordered pairs and triples, and obtain closure under them using the odd numbers. It remains to weed out, as in d26, the unnecessary sets so as to satisfy the axiom of extensionality.

The decision procedures to be described in this paper constitute simplifications of methods previously developed by G. H. von Wright. The decision problems for both the systems under consideration have already been solved, but the known solutions are hopelessly impractical. Our methods for S4 and M, while not “practical” in the sense that they can be applied quickly and easily to any formula, do constitute a vast improvement over any other known methods. It appears, for example, that our methods (with the aid of very little ingenuity) will yield decisions readily when applied to modal functions of degree two (or less) with three (or fewer) distinct propositional variables.