Published online by Cambridge University Press: 12 March 2014
The complete diagram of a structure 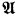 , denoted by Dc(
, denoted by Dc(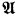 ), is the set of all sentences true in the structure (
), is the set of all sentences true in the structure (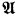 , a)a∈
, a)a∈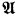 . A structure
. A structure 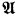 is said to be resplendent if for every sentence θ involving a new relation symbol R in addition to symbols occurring in Dc(
is said to be resplendent if for every sentence θ involving a new relation symbol R in addition to symbols occurring in Dc(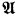 ), if θ is consistent with Dc(
), if θ is consistent with Dc(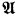 ), then there is a relation P on
), then there is a relation P on 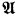 such that
such that 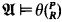 (see[1]).
(see[1]).
Baldwin asked whether a homogeneous recursively saturated structure is necessarily resplendent. Here it is shown that this need not be the case. It is shown that if 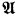 is an uncountable homogeneous resplendent model of an unstable theory, then
is an uncountable homogeneous resplendent model of an unstable theory, then 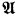 must be saturated. The proof is related to the proof in [5] that an uncountable homogeneous recursively saturated model of first order Peano arithmetic must be saturated. The example for Baldwin's question is an uncountable homogeneous model
must be saturated. The proof is related to the proof in [5] that an uncountable homogeneous recursively saturated model of first order Peano arithmetic must be saturated. The example for Baldwin's question is an uncountable homogeneous model 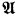 for a particular unstable theory, such that
for a particular unstable theory, such that 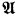 is recursively saturated and omits some type. (The continuum hypothesis is needed to show the existence of such a model in power ℵ1.)
is recursively saturated and omits some type. (The continuum hypothesis is needed to show the existence of such a model in power ℵ1.)
The proof of the main result requires two lemmas.