Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T03:41:31.880Z Has data issue: false hasContentIssue false
  • English
  • Français

A MINIMAL SET LOW FOR SPEED

Part of: Theory of computing Computability and recursion theory

Published online by Cambridge University Press:  03 January 2022

ROD DOWNEY  and
MATTHEW HARRISON-TRAINOR
ROD DOWNEY
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY OF WELLINGTONWELLINGTON, NEW ZEALAND
MATTHEW HARRISON-TRAINOR*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MICHIGANANN ARBOR, MICHIGAN
*
E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An oracle A is low-for-speed if it is unable to speed up the computation of a set which is already computable: if a decidable language can be decided in time $t(n)$ using A as an oracle, then it can be decided without an oracle in time 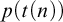$p(t(n))$ for some polynomial p. The existence of a set which is low-for-speed was first shown by Bayer and Slaman who constructed a non-computable computably enumerable set which is low-for-speed. In this paper we answer a question previously raised by Bienvenu and Downey, who asked whether there is a minimal degree which is low-for-speed. The standard method of constructing a set of minimal degree via forcing is incompatible with making the set low-for-speed; but we are able to use an interesting new combination of forcing and full approximation to construct a set which is both of minimal degree and low-for-speed.

Keywords

minimal degreelow for speed

MSC classification

Primary: 03D28: Other Turing degree structures
Secondary: 68Q15: Complexity classes (hierarchies, relations among complexity classes, etc.)
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 4 , December 2022 , pp. 1693 - 1728
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allender, E., Buhrman, H., and Koucký, M., What can be efficiently reduced to the Kolmogorov-random strings? Annals of Pure and Applied Logic , vol. 138 (2006), nos. 1–3, pp. 2–19.CrossRefGoogle Scholar
Allender, E., Friedman, L., and Gasarch, W., Limits on the computational power of random strings . Information and Computation , vol. 222 (2013), pp. 80–92.CrossRefGoogle Scholar
Baker, T., Gill, J., and Solovay, R., Relativizations of the  $\mathbf{\mathcal{P}} = ?\,\mathbf{\mathcal{NP}}$  question . SIAM Journal on Computing , vol. 4 (1975), no. 4, pp. 431–442.CrossRefGoogle Scholar
Bayer, R. E., Lowness for computational speed , Ph.D. thesis, University of California, Berkeley, and ProQuest LLC, 2012.Google Scholar
Bienvenu, L. and Downey, R., On low for speed oracles , Journal of Computer and System Sciences , vol. 108 (2020), pp. 49–63.CrossRefGoogle Scholar
Cai, M., Downey, R. G., Epstein, R., Lempp, S., and Miller, J. S., Random strings and truth-table degrees of Turing complete c.e. sets . Logical Methods in Computer Science , vol. 10 (2014), no. 3:15, 24 pp.CrossRefGoogle Scholar
Slaman, T. A. and Solovay, R., When oracles do not help , COLT (Warmuth, M. K. and Valiant, L. G., editors), Morgan Kaufmann, Oxford, 1991, pp. 379–383.CrossRefGoogle Scholar