Published online by Cambridge University Press: 12 March 2014
Let PA be first order Peano arithmetic, let Λ be the lattice of Π1 sentences modulo PA, and let S be the poset of prime filters of Λ ordered by reverse inclusion. We show there are large convex discrete parts of S; in particular there are convex parts which form a completed Baire tree or an Aronszajn tree.
The elements of S, which we call nodes, correspond to the extensions of PA which are complete for 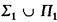 sentences. Equivalently, for each model
sentences. Equivalently, for each model 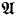 of PA the Π1-theory ∀(
of PA the Π1-theory ∀(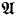 ) of
) of 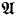 is a node, and every node occurs in this form. Note that the Π1-theory ∀(
is a node, and every node occurs in this form. Note that the Π1-theory ∀(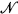 ) of the standard model
) of the standard model 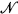 (i.e. the filter of true Π1 sentences) is the unique root of S.
(i.e. the filter of true Π1 sentences) is the unique root of S.
This poset S, which is sometimes called the E-tree, was first studied in [1] where it is shown that:
(1) The poset is tree-like, i.e. the set of predecessors of any node is linearly ordered.
(2) The poset has 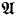 branches, each of which is closed under unions and intersections; in particular each branch has a maximum member.
branches, each of which is closed under unions and intersections; in particular each branch has a maximum member.
(3) There are branches on which ∀(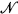 ) does not have an immediate successor. Further properties of the E-tree are given in [2]−[7]. In particular in [4] Misercque shows that:
) does not have an immediate successor. Further properties of the E-tree are given in [2]−[7]. In particular in [4] Misercque shows that:
(4) There are branches on which ∀(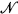 ) does have an immediate successor.
) does have an immediate successor.
(5) There are nodes with both an immediate predecessor and an immediate successor.
The two results (3) and (4) show that there are fundamentally different branches of S, and (5) shows that parts of branches may be discrete.