Article contents
Inequivalent representations of geometric relation algebras
Published online by Cambridge University Press: 12 March 2014
Abstract
It is shown that the automorphism group of a relation algebra 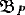 constructed from a projective geometry P is isomorphic to the collineation group of P. Also, the base automorphism group of a representation of
constructed from a projective geometry P is isomorphic to the collineation group of P. Also, the base automorphism group of a representation of 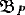 over an affine geometry D is isomorphic to the quotient of the collineation group of D by the dilatation subgroup. Consequently, the total number of inequivalent representations of
over an affine geometry D is isomorphic to the quotient of the collineation group of D by the dilatation subgroup. Consequently, the total number of inequivalent representations of 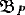 , for finite geometries P, is the sum of the numbers
, for finite geometries P, is the sum of the numbers
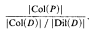
where D ranges over a list of the non-isomorphic affine geometries having P as their geometry at infinity. This formula is used to compute the number of inequivalent representations of relation algebras constructed over projective lines of order at most 10. For instance, the relation algebra constructed over the projective line of order 9 has 56,700 mutually inequivalent representations.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2003
References
REFERENCES
- 1
- Cited by


