Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-02T11:50:24.139Z Has data issue: false hasContentIssue false
  • English
  • Français

The classification of small weakly minimal sets. III: Modules

Published online by Cambridge University Press:  12 March 2014

Steven Buechler
Steven Buechler*
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720
*
Department of Mathematical Sciences, University of Wisconsin—Milwaukee, Milwaukee, Wisconsin 53201
Get access Rights & Permissions [Opens in a new window]

Abstract

Theorem A. Let M be a left R-module such that Th(M) is small and weakly minimal, but does not have Morley rank 1. Let A = acl(∅) ⋂ M and I = {r ∈ R: rM ⊂ A}. Notice that I is an ideal.

(i) F = R/Iis a finite field.

(ii) Suppose that a, b0,…,bn, ∈ M and 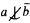. Then there are s, ri ∈ R, i ≤ n, such that sa + Σi≤nribi ∈ A and s ∉ I.

It follows from Theorem A that algebraic closure in M is modular. Using this and results in [B1] and [B2], we obtain

Theorem B. Let M be as in Theorem A. Then Vaught's conjecture holds for Th(M).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 3 , September 1988 , pp. 975 - 979
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bl]Buechler, S., The classification of small weakly minimal sets. I, Proceedings of the U.S.-Israel joint workshop in model theory (Chicago, 1985), Springer-Verlag, Berlin (to appear).Google Scholar
[B2]Buechler, S., The classification of small weakly minimal sets. II, this Journal, vol. 53 (1988), pp. 625–635.Google Scholar
[B3]Buechler, S., The geometry of weakly minimal types, this Journal, vol. 50 (1985), pp. 1044–1053.Google Scholar
[BCM]Baur, W., Cherlin, G., and Macintyre, A., Totally categorical groups and rings, Journal of Algebra, vol. 57 (1979), pp. 407–440.CrossRefGoogle Scholar
[BL]Berline, Ch. and Lascar, D., Superstable groups, Annals of Pure and Applied Logic, vol. 30 (1986), pp. 1–44.CrossRefGoogle Scholar
[Hr]Hrushovski, E., Locally modular regular types, Proceedings of the U.S.-Israel joint workshop in model theory (Chicago, 1985), Springer-Verlag, Berlin (to appear).Google Scholar
[M]Makkai, M., Basic stability theory, with a particular emphasis on orthogonality and regular types, Israel Journal of Mathematics, vol. 49 (1984), pp. 181–238.CrossRefGoogle Scholar
[PP]Pillay, A. and Prest, M., Modules and stability theory, Transactions of the American Mathematical Society, vol. 300 (1987), pp. 641–662.CrossRefGoogle Scholar
[R]Rothmaler, Ph., On a certain ideal, Contributions to general algebra (proceedings, Salzburg, 1986), Hölder-Pichler-Tempsky, Vienna, and Teubner, Stuttgart (to appear).Google Scholar
[Z]Ziegler, M., Model theory of modules, Annals of Pure and Applied Logic, vol. 26 (1984), pp. 149–213.CrossRefGoogle Scholar