Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T17:32:16.348Z Has data issue: false hasContentIssue false
  • English
  • Français

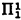Two interpolation theorems for a predicate calculus1

Published online by Cambridge University Press:  12 March 2014

Shoji Maehara  and
Gaisi Takeuti
Shoji Maehara
Affiliation:
University of Illinois, Urbana, Illinois 61801
Gaisi Takeuti
Affiliation:
University of Illinois, Urbana, Illinois 61801
Get access Rights & Permissions [Opens in a new window]

Extract

A second order formula is called Π1 if, in its prenex normal form, all second order quantifiers are universal. A sequent F1, … Fm → G1 …, Gn is called Π1 if a formula

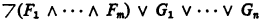
is Π1

If we consider only Π1 sequents, then we can easily generalize the completeness theorem for the cut-free first order predicate calculus to a cut-free Π1 predicate calculus.

In this paper, we shall prove two interpolation theorems on the Π1 sequent, and show that Chang's theorem in [2] is a corollary of our theorem. This further supports our belief that any form of the interpolation theorem is a corollary of a cut-elimination theorem. We shall also show how to generalize our results for an infinitary language. Our method is proof-theoretic and an extension of a method introduced in Maehara [5]. The latter has been used frequently to prove the several forms of the interpolation theorem.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 2 , June 1971 , pp. 262 - 270
Copyright
Copyright © Association for Symbolic Logic 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Part of this work was supported by NSF GP 14134.

References

[1]Chang, C. C., A generalization of the Craig interpolation theorem. Notices of the American Mathematical Society, vol. 15 (1968), p. 934.Google Scholar
[2]Chang, C. C., Two interpolation theorems, Proceedings of a conference in model theory, University of Rome, 11 17–20, 1969 (to appear).Google Scholar
[3]Kueker, D. W., Generalized interpolation and definability (to appear in Annals of Mathematical Logic).Google Scholar
[4]Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas, Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
[5]Maehara, S., Craig's interpolation theorem, Sŭgaku (1961), pp. 235–237 (Japanese).Google Scholar