Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T07:48:02.901Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBCOMPLETE FORCING, TREES, AND GENERIC ABSOLUTENESS

Published online by Cambridge University Press:  23 October 2018

GUNTER FUCHS  and
KAETHE MINDEN
GUNTER FUCHS
Affiliation:
MATHEMATICS, THE GRADUATE CENTER OF THE CITY UNIVERSITY OF NEW YORK, 365 FIFTH AVENUE, NEW YORK, NY 10016, USA and MATHEMATICS, COLLEGE OF STATEN ISLAND OF CUNY, STATEN ISLAND, NY10314, USAE-mail: [email protected]: http://www.math.csi.cuny/edu/∼fuchs
KAETHE MINDEN
Affiliation:
MATHEMATICS, MARLBORO COLLEGE, 2582 SOUTH ROAD, MARLBORO, VT05344, USA E-mail: [email protected]: https://kaetheminden.wordpress.com/
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate properties of trees of height ω1 and their preservation under subcomplete forcing. We show that subcomplete forcing cannot add a new branch to an ω1-tree. We introduce fragments of subcompleteness which are preserved by subcomplete forcing, and use these in order to show that certain strong forms of rigidity of Suslin trees are preserved by subcomplete forcing. Finally, we explore under what circumstances subcomplete forcing preserves Aronszajn trees of height and width ω1. We show that this is the case if CH fails, and if CH holds, then this is the case iff the bounded subcomplete forcing axiom holds. Finally, we explore the relationships between bounded forcing axioms, preservation of Aronszajn trees of height and width ω1 and generic absoluteness of 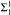${\rm{\Sigma }}_1^1$-statements over first order structures of size ω1, also for other canonical classes of forcing.

Keywords

03E5003E5703E3503E5503E05subcomplete forcingforcing axiomsgeneric absolutenessSuslin treescontinuum hypothesis
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 3 , September 2018 , pp. 1282 - 1305
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J., Bounded forcing axioms as principles of generic absoluteness. Archive for Mathematical Logic, vol. 39 (2000), pp. 393–401.CrossRefGoogle Scholar
Friedman, H., On closed sets of ordinals. Proceedings of the American Mathematical Society, vol. 43 (1974), no. 1, pp. 190–192.CrossRefGoogle Scholar
Fuchs, G., Closed maximality principles: Implications, separations and combinations, this JOURNAL, vol. 73 (2008), no. 1, pp. 276–308.Google Scholar
Fuchs, G., Hierarchies of forcing axioms, the continuum hypothesis and square principles, this JOURNAL, vol. 83 (2018), no. 1, pp. 256–282.Google Scholar
Fuchs, G., Hierarchies of (virtual) resurrection axioms, this JOURNAL, vol. 83 (2018), no. 1, pp. 283–325.Google Scholar
Fuchs, G., Closure properties of parametric subcompleteness. Archive for Mathematical Logic, 2018, https://doi.org/10.1007/s00153-018-0611-x.CrossRefGoogle Scholar
Fuchs, G. and Hamkins, J. D., Degrees of rigidity for Souslin trees, this JOURNAL, vol. 74 (2009), no. 2, pp. 423–454.Google Scholar
Fuchs, G. and Rinot, A., Weak square and stationary reflection. Acta Mathematica Hungarica, 2018, https://doi.org/10.1007/s10474-018-0789-8.CrossRefGoogle Scholar
Goldstern, M. and Shelah, S., The bounded proper forcing axiom, this JOURNAL, vol. 60 (1995), no. 1, pp. 58–73.Google Scholar
Jensen, R. B., Forcing axioms compatible with CH, handwritten notes, 2009. Available at https://www.mathematik.hu-berlin.de/∼raesch/org/jensen.html.Google Scholar
Jensen, R. B., Subcomplete forcing and ℒ-forcing, E-Recursion, Forcing and C*-Algebras (Chong, C., Feng, Q., Slaman, T. A., Woodin, W. H., and Yang, Y., editors), Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 27, World Scientific, Singapore, 2014, pp. 83–182.CrossRefGoogle Scholar
Jensen, R. B., On the subcompleteness of some Namba-type forcings, handwritten notes, 2017. Available at https://www.mathematik.hu-berlin.de/∼raesch/org/jensen.html.Google Scholar
Mildenberger, H. and Shelah, S., Specialising Aronszajn trees and preserving some weak diamonds. Journal of Applied Analysis, vol. 15 (2009), no. 1, pp. 47–78.CrossRefGoogle Scholar
Minden, K., On subcomplete forcing, Ph.D. thesis, The CUNY Graduate Center, 2017. Preprint available from arXiv:1705.00386 [math.LO].Google Scholar