Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-16T23:11:33.820Z Has data issue: false hasContentIssue false
  • English
  • Français

Reverse mathematics and Ramsey's property for trees

Published online by Cambridge University Press:  12 March 2014

Jared Corduan ,
Marcia J. Groszek  and
Joseph R. Mileti
Jared Corduan
Affiliation:
6188 Kemeny Hall, Dartmouth College, Hanover, Nh 03755-3551, USA. E-mail: [email protected]
Marcia J. Groszek
Affiliation:
6188 Kemeny Hall, Dartmouth College, Hanover, Nh 03755-3551, USA. E-mail: [email protected]
Joseph R. Mileti
Affiliation:
Department of Mathematics and Statistics, Grinnell College, Grinnell, Ia 50112-1690, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

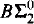We show, relative to the base theory RCA0: A nontrivial tree satisfies Ramsey's Theorem only if it is biembeddable with the complete binary tree. There is a class of partial orderings for which Ramsey's Theorem for pairs is equivalent to ACA0. Ramsey's Theorem for singletons for the complete binary tree is stronger than . hence stronger than Ramsey's Theorem for singletons for ω. These results lead to extensions of results, or answers to questions, of Chubb, Hirst, and McNicholl [3].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 3 , September 2010 , pp. 945 - 954
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cholak, P., Jockusch, C., and Slaman, T., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[2]Chong, C. T. and Yang, Y., Σ2 induction and infinite injury priority argument, I. Maximal sets and the jump operator, this Journal, vol. 63 (1998), no. 3, pp. 797–814.Google Scholar
[3]Chubb, J., Hirst, J., and McNicholl, T., Reverse mathematics, computability, and partitions of trees, this Journal, vol. 74 (2009), no. 1, pp. 201–215.Google Scholar
[4]Hirst, J., Combinatorics in subsystems of second order arithmetic, Ph.D. thesis, The Pennsylvania State University, 1987.Google Scholar
[5]Hirst, J., personal communication (e-mail 06 12, 2008).Google Scholar
[6]Simpson, S., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1999.CrossRefGoogle Scholar