Published online by Cambridge University Press: 12 March 2014
We work in set-theory without choice ZF . A set is countable if it is finite or equipotent with ℕ. Given a closed subset F of [0, 1]I which is a bounded subset of ℓ 1(I) (resp. such that F ⊆ c 0(I)), we show that the countable axiom of choice for finite sets, (resp. the countable axiom of choice AC ℕ) implies that F is compact. This enhances previous results where AC ℕ (resp. the axiom of Dependent Choices) was required. If I is linearly orderable (for example I = ℝ), then, in ZF , the closed unit ball of the Hilbert space ℓ 2 (I) is (Loeb-)compact in the weak topology. However, the weak compactness of the closed unit ball of 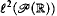 is not provable in ZF .
is not provable in ZF .