Published online by Cambridge University Press: 12 March 2014
In [1], various formal proof systems for infinitary formulas were defined. The formal proof system 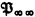 is the result of extending the basic predicate calculus
is the result of extending the basic predicate calculus 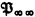 by adding a collection Σ of axiom schemes and a collection Ω of rules of inference. Let Taut be the collection of all infinitary prepositional tautologies, considered as axiom schemes. Let ΩI consist of all the quantificational rules of independent choices. We will show, in §2 (see Theorem 2.1), that
by adding a collection Σ of axiom schemes and a collection Ω of rules of inference. Let Taut be the collection of all infinitary prepositional tautologies, considered as axiom schemes. Let ΩI consist of all the quantificational rules of independent choices. We will show, in §2 (see Theorem 2.1), that 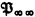 (Taut; 0) is not complete for L∞ω (i.e., infinitary finite-quantifier) sentences; that is, we will exhibit an L∞ω sentence ϕ such that ¬ϕ is true in all models, but ¬ϕ is not provable in
(Taut; 0) is not complete for L∞ω (i.e., infinitary finite-quantifier) sentences; that is, we will exhibit an L∞ω sentence ϕ such that ¬ϕ is true in all models, but ¬ϕ is not provable in 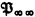 (Taut; 0). (The unprovability is shown by a weak forcing version of Boolean general models.) This answers a question of Karp in [1,12.1(i)]. In §4, we will show that our ϕ is “
(Taut; 0). (The unprovability is shown by a weak forcing version of Boolean general models.) This answers a question of Karp in [1,12.1(i)]. In §4, we will show that our ϕ is “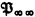 complete for L∞ω ) sentences.”
complete for L∞ω ) sentences.”