Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T23:51:32.655Z Has data issue: false hasContentIssue false
  • English
  • Français

Fragments of bounded arithmetic and the lengths of proofs

Published online by Cambridge University Press:  12 March 2014

Pavel Pudlák
Pavel Pudlák*
Affiliation:
Institute of Mathematics, Academy of Sciences, Prague, Czech Republic, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

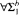We consider the problem whether the theorems of the fragments 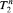form a strictly increasing hierarchy. We shall show a link to some results about the lengths of proofs in predicate logic that supports the conjecture that the hierarchy is strictly increasing.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 4 , December 2008 , pp. 1389 - 1406
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buss, S. R., Bounded arithmetic, Bibliopolis, 1986.Google Scholar
[2]Buss, S. R., An introduction to proof theory, Handbook of proof theory, Elsevier, 1998, pp. 1–78.Google Scholar
[3]Buss, S. R. and Krajíček, J., An application of boolean complexity to separation problems in bounded arithmetic, Proceedings of the London Mathematical Society, vol. 69 (1994), no. 3, pp. 1–21.CrossRefGoogle Scholar
[4]Hanika, J., Herbrandizing search problems in bounded arithmetic, Mathematical Logic Quarterly, vol. 50 (2004), no. 6, pp. 577–586.CrossRefGoogle Scholar
[5]Hetzl, S., Describing proofs by short tautologies, preprint, 2007.Google Scholar
[6]Krajíček, J., No counter-example interpretation and interactive computations, Logic from computer science (Moschovakis, Y. N., editor), Springer-Verlag, 1992, pp. 287–293.CrossRefGoogle Scholar
[7]Krajíček, J., Bounded arithmetic, propositional logic, and complexity theory, Encyclopedia of Mathematics and its Applications, vol. 60, Cambridge University Press, 1995.CrossRefGoogle Scholar
[8]Krajíček, J. and Pudlák, P., Quantified propositional calculi andfragments of bounded arithmetic, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 36 (1990), pp. 29–46.CrossRefGoogle Scholar
[9]Krajíček, J., Pudlák, P., and Takeuti, G., Bounded arithmetic and the polynomial hierarchy, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 143–153.CrossRefGoogle Scholar
[10]Krajíček, J. and Takeuti, G., On induction-free provability, Annals of Mathematics and Artificial Intelligence, vol. 6 (1992), pp. 107–126.CrossRefGoogle Scholar
[11]Orevkov, V. P., Lower bounds on the increase in complexity of deductions in cut elimination, Soviet Mathematics, vol. 20, Original Russian version in Zapiski Nauchnych Seminarov LOMI, vol. 88, (1979), pp. 137–162.Google Scholar
[12]Pudlák, P., Some relations between subsystems of arithmetic and the complexity of computations, Logic from computer science (Moschovakis, Y. N., editor), Springer-Verlag, 1992, pp. 308–317.Google Scholar
[13]Pudlák, P., The lengths of proofs, Handbook of proof theory, Elsevier, 1998, pp. 547–637.CrossRefGoogle Scholar
[14]Pudlák, P., Consistency and games—in search of new combinatorial principles, Proceedings of the Logic Colloquium '03 (Stoltenberg-Hansen, V. and Vaananen, J., editors), Association for Symbolic Logic, 2006, pp. 244–281.CrossRefGoogle Scholar
[15]Skelley, A. and Thapen, N., The provably total search problems of bounded arithmetic, preprint, 2007.Google Scholar
[16]Statman, R., Proof search and speed-up in the predicate calculus, Annals of Mathematical Logic, vol. 15 (1978), pp. 225–287.CrossRefGoogle Scholar