Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-21T02:34:55.352Z Has data issue: false hasContentIssue false
  • English
  • Français

First-order and counting theories of ω-automatic structures

Published online by Cambridge University Press:  12 March 2014

Dietrich Kuske  and
Markus Lohrey
Dietrich Kuske
Affiliation:
Universität Leipzig, Institut Für Informatik, Postfach 100920, D-04009 Leipzig, Germany, E-mail: [email protected]
Markus Lohrey
Affiliation:
Universität Leipzig, Institut Für Informatik, Postfach 100920, D-04009 Leipzig, Germany, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The logic 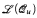extends first-order logic by a generalized form of counting quantifiers (“the number of elements satisfying … belongs to the set C”). This logic is investigated for structures with an injectively ω-automatic presentation. If first-order logic is extended by an infinity-quantifier, the resulting theory of any such structure is known to be decidable [6]. It is shown that, as in the case of automatic structures [21], also modulo-counting quantifiers as well as infinite cardinality quantifiers (“there are 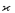many elements satisfying …”) lead to decidable theories. For a structure of bounded degree with injective ω-automatic presentation, the fragment of 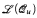that contains only effective quantifiers is shown to be decidable and an elementary algorithm for this decision is presented. Both assumptions (ω-automaticity and bounded degree) are necessary for this result to hold.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 1 , March 2008 , pp. 129 - 150
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bárány, V., Automatic presentations of infinite structures, Ph.D. thesis, RWTH Aachen, Fakultät für Mathematik, Informatik und Naturwissenschaften, 2007.Google Scholar
[2]Benedikt, M., Libkin, L., Schwentick, T., and Segoufin, L., Definable relations and first-order query languages over strings, Journal of the ACM, vol. 50 (2003), no. 5, pp. 694–751.CrossRefGoogle Scholar
[3]Bès, A., Undecidable extensions of Biichi arithmetic and Cobham-Semenov theorem, this Journal, vol. 62 (1997), no. 4, pp. 1280–1296.Google Scholar
[4]Blumensath, A., Automatic structures, Technical report, RWTH Aachen, 1999.Google Scholar
[5]Blumensath, A. and Grädel, E., Automatic structures, Proceedings of the IEEE Symposium on Logic in Computer Science (LICS), EEE Computer Society, 2000, pp. 51–62.Google Scholar
[6]Blumensath, A. and Grädel, E., Finite presentations of infinite structures: Automata and interpretations, Theory of Computing Systems, vol. 37 (2004), no. 6, pp. 641–674.CrossRefGoogle Scholar
[7]BüChi, J. R., Weak second-order arithmetic and finite automata, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 6 (1960), pp. 66–92.CrossRefGoogle Scholar
[8]Choueka, Y., Theories of automata on ω-tapes: A simplified approach, Journal of Computer and System Sciences, vol. 8 (1974), pp. 117–141.CrossRefGoogle Scholar
[9]Compton, K. J. and Henson, C. W., A uniform method for proving lower bounds on the computational complexity of logical theories, Annals of Pure and Applied Logic, vol. 48 (1990), pp. 1–79.CrossRefGoogle Scholar
[10]Epstein, D. B. A., Cannon, J. W., Holt, D. F., Levy, S. V. F., Paterson, M. S., and Thurston, W. P., Word Processing in Groups, Jones and Bartlett, Boston, 1992.CrossRefGoogle Scholar
[11]Gaifman, H., On local and nonlocal properties, Logic Colloquium '81 (Stern, J., editor), North-Holland, 1982, pp. 105–135.Google Scholar
[12]Härtig, K., Über einen Quantifikatur mit zwei Wirkungsbereichen, Colloquium on the Foundations of Mathematics, Mathematical Machines and their Applications (Tihany, 1962), Akademiai Kiadó, Budapest, 1965, pp. 31–36.Google Scholar
[13]Hodges, W., Model Theory, Cambridge University Press, 1993.CrossRefGoogle Scholar
[14]Hodgson, B. R., On direct products of automaton decidable theories, Theoretical Computer Science, vol. 19 (1982), pp. 331–335.CrossRefGoogle Scholar
[15]Ishihara, H., Khoussainov, B., and Rubin, S., Some results on automatic structures, Proceedings of the IEEE Symposium on Logic in Computer Science (LICS), EEE Computer Society, 2002, pp. 235–244.Google Scholar
[16]Keisler, H. J. and Lotfallah, W. B., A local normal form theorem for infinitary logic with unary quantifiers, Mathematical Logic Quarterly, vol. 51 (2005), no. 2, pp. 137–144.CrossRefGoogle Scholar
[17]Khoussainov, B., Hjorth, G., Montalban, A., and Nies, A., From automatic structures to Borel structures, 2007, manuscript.Google Scholar
[18]Khoussainov, B. and Nerode, A., Automatic presentations of structures, LCC: International Workshop on Logic and Computational Complexity (Leivant, Daniel, editor), Lecture Notes in Computer Science, vol. 960, Springer, 1994, pp. 367–392.CrossRefGoogle Scholar
[19]Khoussainov, B. and Rubin, S., Graphs with automatic presentations over a unary alphabet, Journal of Automata, Languages and Combinatorics, vol. 6 (2001), no. 4, pp. 467–480.Google Scholar
[20]Khoussainov, B., Rubin, S., and Stephan, F., Automatic partial orders, Proceedings of the IEEE Symposium on Logic in Computer Science (LICS), EEE Computer Society, 2003, pp. 168–177.Google Scholar
[21]Khoussainov, B., Rubin, S., and Stephan, F., Definability and regularity in automatic structures, Proceedings of the Symposium on Theoretical Aspects of Computer Science (STACS) (Diekert, Volker and Habib, Michel, editors), Lecture Notes in Computer Science, vol. 2996, Springer, 2004, pp. 440–451.Google Scholar
[22]Kuske, D., Is Cantor's theorem automatic, Proceedings of the International Conference on Logic for Programming, Artificial Intelligence, and Reasoning (LPAR) (Vardi, Moshe Y. and Voronkov, Andrei, editors), Lecture Notes in Artificial Intelligence, vol. 2850, Springer, 2003, pp. 332–345.Google Scholar
[23]Kuske, D. and Lohrey, M., First-order and counting theories of ω-automatic structures, Proceedings of the 9th International Conference on Foundations of Software Science and Computation Structures (FOSSACS) (Aceto, Luca and Ingólfsdóttir, Anna, editors), Lecture Notes in Computer Science, vol. 3921, Springer, 2006, pp. 322–336.CrossRefGoogle Scholar
[24]Lindner, R. and Staiger, L., Algebraische Codierungstheorie, Akademie-Verlag Berlin, 1977.CrossRefGoogle Scholar
[25]Lohrey, M., Automatic structures of bounded degree, Proceedings of the 10th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning (LPAR) (Vardi, Moshe Y. and Voronkov, Andrei, editors), Lecture Notes in Artificial Intelligence, vol. 2850, Springer, 2003, pp. 344–358.Google Scholar
[26]Papadimitriou, C. H., Computational Complexity, Addison Wesley, 1994.Google Scholar
[27]Perrin, D. and Pin, J.-E., Infinite Words, Pure and Applied Mathematics, vol. 141, Elsevier, 2004.Google Scholar
[28]Stockmeyer, L.J. and Meyer, A. R., Word problems requiring exponential time (preliminary report), Proceedings of the ACM Symposium on Theory of Computing (STOC), 1973, pp. 1–9.Google Scholar
[29]Tao, Y., Infinity problems and countability problems for ω-automata, Information Processing Letters, vol. 100 (2006), no. 4, pp. 151–153.CrossRefGoogle Scholar
[30]Thomas, W., Automata on infinite objects, Handbook of Theoretical Computer Science (van Leeuwen, J., editor), Elsevier Science Publishers B. V., 1990, pp. 133–191.Google Scholar