Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T20:13:59.339Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS

Part of: Computability and recursion theory Special aspects of infinite or finite groups

Published online by Cambridge University Press:  22 October 2020

ARMAN DARBINYAN
ARMAN DARBINYAN*
Affiliation:
DEPARTMENT OF MATHEMATICS TEXAS A&M UNIVERSITYCOLLEGE STATION, TX, MAILSTOP 3368, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The main objective of this paper is the following two results. (1) There exists a computable bi-orderable group that does not have a computable bi-ordering; (2) there exists a bi-orderable, two-generated computably presented solvable group with undecidable word problem. Both of the groups can be found among two-generated solvable groups of derived length 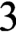$3$.

(1) [a]nswers a question posed by Downey and Kurtz; (2) answers a question posed by Bludov and Glass in Kourovka Notebook.

One of the technical tools used to obtain the main results is a computational extension of an embedding theorem of B. Neumann that was studied by the author earlier. In this paper we also compliment that result and derive new corollaries that might be of independent interest.

Keywords

computable structure theorycomputable groupscomputable ordersorderable groups

MSC classification

Primary: 20F10: Word problems, other decision problems, connections with logic and automata
Secondary: 20F60: Ordered groups 03D45: Theory of numerations, effectively presented structures
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 4 , December 2020 , pp. 1588 - 1598
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bludov, V. V. and Glass, A. M. W., Word problems, embeddings, and free products of right ordered groups with amalgamated subgroup. The Proceedings of the London Mathematical Society, vol. 99 (2009), pp. 585–608.CrossRefGoogle Scholar
Darbinyan, A., Group embeddings with algorithmic properties. Communications in Algebra, vol. 43 (2015), no. 11, pp. 4923–4935.CrossRefGoogle Scholar
Darbinyan, A., Computable groups which do not embed into groups with decidable conjugacy problem. Inventiones Mathematicae, to appear. DOI:10.1007/s00222-020-01022-0, arXiv:1708.09047CrossRefGoogle Scholar
Downey, R. G. and Remmel, J. B., Questions in computable algebra and combinatorics, Computability Theory and Its Applications, Contemporary Mathematics, vol. 257, American Mathematical Society, Providence, RI, 2000, pp. 95–125.CrossRefGoogle Scholar
Harrison-Trainor, M., Left-orderable computable groups, this Journal, vol. 81 (2018), no. 1, pp. 237–255.Google Scholar
Kharlampovich, O., A finitely presented solvable group with non-solvable word problem. Izvestiya Rossiiskoi Akademii Nauk. Seriya Matematicheskaya, vol. 45 (1981), no. 4, pp. 852–873.Google Scholar
Kourovka Notebook, Unsolved Problems in Group Theory, fifth ed., Novosibirsk, Russia, 1976.Google Scholar
Mal'cev, A., Constructive algebras. I. Uspekhi Matematicheskikh Nauk, vol. 16 (1961), no. 3, pp. 3–60.Google Scholar
Neumann, B. H., Embedding theorems for ordered groups. Journal of the London Mathematical Society, vol. 1 (1960), no. 4, pp. 503–512.CrossRefGoogle Scholar
Rabin, M., Computable algebra, general theory and theory of computable fields. Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
Shoenfield, J. R., Mathematical Logic, Addison Wesley, Boston, MA, 1967.Google Scholar
Smullyan, R. M., Undecidability and recursive inseparability. Mathematical Logic Quarterly, vol. 4 (1958), no. 7–11, pp. 143–147.CrossRefGoogle Scholar
Solomon, R., Π10 classes and orderable groups. Annals of Pure and Applied Logic, vol. 115 (2002), no. 1–3, pp. 279–302.CrossRefGoogle Scholar