Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elwes, Richard
Lewis-Pye, Andy
Löwe, Benedikt
Macpherson, Dugald
Normann, Dag
Sorbi, Andrea
Soskova, Alexandra A.
Soskova, Mariya I.
van Emde Boas, Peter
Wainer, Stan
and
Löwe, Benedikt
2018.
S. Barry Cooper (1943–2015).
Computability,
Vol. 7,
Issue. 2-3,
p.
103.
Lempp, Steffen
Slaman, Theodore A.
and
Soskova, Mariya I.
2021.
Fragments of the theory of the enumeration degrees.
Advances in Mathematics,
Vol. 383,
Issue. ,
p.
107686.
Goh, Jun Le
Lempp, Steffen
Ng, Keng Meng
Soskova, Mariya I.
Brattka, Vasco
Greenberg, Noam
Kalimullin, Iskander
and
Soskova, Mariya
2022.
Extensions of two constructions of Ahmad.
Computability,
Vol. 11,
Issue. 3-4,
p.
269.
KALIMULLIN, ISKANDER SH.
LEMPP, STEFFEN
NG, KENG
and
YAMALEEV, MARS M.
2024.
ON CUPPING AND AHMAD PAIRS.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 3,
p.
1358.
Jacobsen-Grocott, Josiah
2024.
Strong minimal pairs in the enumeration degrees.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 10,
p.
103464.


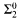 -enumeration degrees is undecidable
-enumeration degrees is undecidable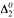 -degrees is undecidable.
-degrees is undecidable.