Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T21:38:12.342Z Has data issue: false hasContentIssue false
  • English
  • Français

THE Σ1-DEFINABLE UNIVERSAL FINITE SEQUENCE

Part of: Set theory Nonstandard models

Published online by Cambridge University Press:  08 January 2021

JOEL DAVID HAMKINS  and
KAMERYN J. WILLIAMS
JOEL DAVID HAMKINS
Affiliation:
UNIVERSITY OF OXFORD FACULTY OF PHILOSOPHY RADCLIFFE OBSERVATORY QUARTER 555 WOODSTOCK ROAD OXFORD, OX2 6GG, UK and UNIVERSITY COLLEGE HIGH STREET OXFORD, OX1 4BH, UKE-mail:[email protected]: http://jdh.hamkins.org
KAMERYN J. WILLIAMS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF HAWAI‘I AT MĀNOA 2565 MCCARTHY MALL KELLER 401A HONOLULU, HI 96822, USAE-mail:[email protected]: http://kamerynjw.net
Get access Rights & Permissions [Opens in a new window]

Abstract

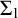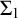We introduce the $\Sigma _1$ -definable universal finite sequence and prove that it exhibits the universal extension property amongst the countable models of set theory under end-extension. That is, (i) the sequence is $\Sigma _1$ -definable and provably finite; (ii) the sequence is empty in transitive models; and (iii) if M is a countable model of set theory in which the sequence is s and t is any finite extension of s in this model, then there is an end-extension of M to a model in which the sequence is t. Our proof method grows out of a new infinitary-logic-free proof of the Barwise extension theorem, by which any countable model of set theory is end-extended to a model of 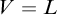$V=L$ or indeed any theory true in a suitable submodel of the original model. The main theorem settles the modal logic of end-extensional potentialism, showing that the potentialist validities of the models of set theory under end-extensions are exactly the assertions of S4. Finally, we introduce the end-extensional maximality principle, which asserts that every possibly necessary sentence is already true, and show that every countable model extends to a model satisfying it.

Keywords

potentialismend-extensions of models of set theorymaximality principles

MSC classification

Primary: 03H05: Nonstandard models in mathematics
Secondary: 03E40: Other aspects of forcing and Boolean-valued models 03E45: Inner models, including constructibility, ordinal definability, and core models
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 2 , June 2022 , pp. 783 - 801
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barwise, J., Infinitary methods in the model theory of set theory , Logic Colloquium ’69 (Proc. Summer School and Colloq., Manchester, 1969) , North-Holland, Amsterdam, 1971, pp. 53–66.Google Scholar
Blanck, R., Contributions to the metamathematics of arithmetic. Fixed points, independence, and flexibility , Ph.D. thesis, University of Gothenburg, 2017. http://hdl.handle.net/2077/52271.Google Scholar
Blanck, R. and Enayat, A., Marginalia on a theorem of Woodin , this Journal, vol. 82 (2017), no. 1, pp. 359–374.Google Scholar
Friedman, S.-D., Kanovei, V., and Gitman, V., A model of second-order arithmetic satisfying AC but not DC . Journal of Mathematical Logic , vol. 19 (2019), no. 1, pp. 1850013.CrossRefGoogle Scholar
Gitman, V., Hamkins, J. D., and Johnstone, T. A., What is the theory ZFC without powerset? Mathematical Logic Quarterly , vol. 62 (2016), no. 4–5, pp. 391–406.10.1002/malq.201500019CrossRefGoogle Scholar
Hamkins, J. D., A multiverse perspective on the axiom of constructibility, Infinity and Truth, Lecture Notes Series, vol. 25, Institute for Mathematical Sciences, National University of Singapore, World Scientific, Hackensack, NJ, 2014, pp. 25–45.CrossRefGoogle Scholar
Hamkins, J. D., A new proof of the Barwise extension theorem, without infinitary logic. Mathematics and Philosophy of the Infinite. 2018. http://jdh.hamkins.org/a-new-proof-of-the-barwise-extension-theorem/ (version 27 July 2018).Google Scholar
Hamkins, J. D., The modal logic of arithmetic potentialism and the universal algorithm, arXiv preprint, 2018, arXiv:1801.04599 [math.LO], under review http://wp.me/p5M0LV-1zz.Google Scholar
Hamkins, J. D. and Linnebo, Ø., The modal logic of set-theoretic potentialism and the potentialist maximality principles. Review of Symbolic Logic , vol. 15 (2022), no. 1, pp. 1–35.Google Scholar
Hamkins, J. D. and Woodin, W. H., The universal finite set, arXiv preprint, 2017, arXiv:1711.07952 [math.LO], manuscript under review. http://jdh.hamkins.org/the-universal-finite-set.Google Scholar
Kaufmann, M., On existence of $\Sigma _n$ end extensions, Logic Year 1979–80 (Proc. Seminars and Conf. Math. Logic, Univ. Connecticut, Conn., 1979/90) , Lecture Notes in Mathematics, vol. 859, Springer, Berlin, 1981, pp. 92–103.Google Scholar
Keisler, H. J. and Morley, M., Elementary extensions of models of set theory . Israel Journal of Mathematics , vol. 6 (1968), pp. 49–65.CrossRefGoogle Scholar
Linnebo, Ø., The potential hierarchy of sets . Review of Symbolic Logic , vol. 6 (2013), no. 2 pp. 205–228.CrossRefGoogle Scholar
Linnebo, Ø. and Shapiro, S., Actual and potential infinity . Noûs , vol. 53 (2019), no. 1, pp. 160–191.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , second ed., Perspectives in Logic, Cambridge University Press, Association for Symbolic Logic, Cambridge, 2009.10.1017/CBO9780511581007CrossRefGoogle Scholar
Woodin, W. H., A potential subtlety concerning the distinction between determinism and nondeterminism , Infinity , Cambridge University Press, Cambridge, 2011, pp. 119–129.10.1017/CBO9780511976889.007CrossRefGoogle Scholar
Zarach, A., Unions of ZF− -models which are themselve ZF− -models , Logic Colloquium ’80 (Van Dalen, D., Lascar, D., and Smiley, T. J., editor), Studies in Logic and the Foundations of Mathematics, vol. 108, Elsevier, Amsterdam, 1982, pp. 315–342.Google Scholar
Zarach, A. M., Replacement ↛ collection , Gödel ’96 (Brno, 1996) , Lecture Notes Logic, vol. 6, Springer, Berlin, 1996, pp. 307–322.10.1007/978-3-662-21963-8_22CrossRefGoogle Scholar