Published online by Cambridge University Press: 30 July 2015
The origin of the 22-year solar magnetic cycle lies below the photosphere where multiscale plasma motions, due to turbulent convection, produce magnetic fields. The most powerful intensity and velocity signals are associated with convection cells, called granules, with a scale of typically 1 Mm and a lifetime of a few minutes. Small-scale magnetic elements (SMEs), ubiquitous on the solar photosphere, are passively transported by associated plasma flows. This advection makes their traces very suitable for defining the convective regime of the photosphere. Therefore the solar photosphere offers an exceptional opportunity to investigate convective motions, associated with compressible, stratified, magnetic, rotating and large Rayleigh number stellar plasmas. The magnetograms used here come from a Hinode/SOT uninterrupted 25-hour sequence of spectropolarimetric images. The mean-square displacement of SMEs has been modelled with a power law with spectral index 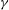 ${\it\gamma}$ . We found
${\it\gamma}$ . We found 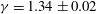 ${\it\gamma}=1.34\pm 0.02$ for times up to
${\it\gamma}=1.34\pm 0.02$ for times up to 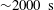 ${\sim}2000~\text{s}$ and
${\sim}2000~\text{s}$ and  ${\it\gamma}=1.20\pm 0.05$ for times up to
${\it\gamma}=1.20\pm 0.05$ for times up to 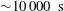 ${\sim}10\,000~\text{s}$ . An alternative way to investigate the advective–diffusive motion of SMEs is to look at the evolution of the two-dimensional probability distribution function (PDF) for the displacements. Although at very short time scales the PDFs are affected by pixel resolution, for times shorter than
${\sim}10\,000~\text{s}$ . An alternative way to investigate the advective–diffusive motion of SMEs is to look at the evolution of the two-dimensional probability distribution function (PDF) for the displacements. Although at very short time scales the PDFs are affected by pixel resolution, for times shorter than 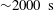 ${\sim}2000~\text{s}$ the PDFs seem to broaden symmetrically with time. In contrast, at longer times a multi-peaked feature of the PDFs emerges, which suggests the non-trivial nature of the diffusion–advection process of magnetic elements. A Voronoi distribution analysis shows that the observed small-scale distribution of SMEs involves the complex details of highly nonlinear small-scale interactions of turbulent convective flows detected in solar photospheric plasma.
${\sim}2000~\text{s}$ the PDFs seem to broaden symmetrically with time. In contrast, at longer times a multi-peaked feature of the PDFs emerges, which suggests the non-trivial nature of the diffusion–advection process of magnetic elements. A Voronoi distribution analysis shows that the observed small-scale distribution of SMEs involves the complex details of highly nonlinear small-scale interactions of turbulent convective flows detected in solar photospheric plasma.