Published online by Cambridge University Press: 10 April 2019
To explain the possible destabilization of a two-dimensional magnetic equilibrium such as the near-Earth magnetotail, we developed a kinetic model describing the resonant interaction of electromagnetic fluctuations and bouncing electrons trapped in the magnetic bottle. A small-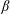 $\unicode[STIX]{x1D6FD}$ approximation (i.e., the plasma pressure is lower than the magnetic pressure) is used in agreement with a small field line curvature. The linearized gyro-kinetic Vlasov equation is integrated along the unperturbed particle trajectories, including cyclotron and bounce motions. The dispersion relation for drift-Alfvèn waves is obtained through the plasma quasi-neutrality condition and Ampere’s law for the parallel current. It has been found that for a quasi-dipolar configuration (
$\unicode[STIX]{x1D6FD}$ approximation (i.e., the plasma pressure is lower than the magnetic pressure) is used in agreement with a small field line curvature. The linearized gyro-kinetic Vlasov equation is integrated along the unperturbed particle trajectories, including cyclotron and bounce motions. The dispersion relation for drift-Alfvèn waves is obtained through the plasma quasi-neutrality condition and Ampere’s law for the parallel current. It has been found that for a quasi-dipolar configuration (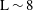 $\text{L}\sim 8$ corresponds to the set of the Earth’s magnetic field lines, crossing the Earths magnetic equator at 8 Earth radii), unstable electromagnetic modes may develop in the current sheet with a growth rate of the order of a few tenths of a second provided that the typical scale of density gradient slope responsible for the diamagnetic drift effects is over one Earth radius or less. This instability growth rate is large enough to destabilize the current sheet on time scales of 2–4 minutes as observed during substorm onset.
$\text{L}\sim 8$ corresponds to the set of the Earth’s magnetic field lines, crossing the Earths magnetic equator at 8 Earth radii), unstable electromagnetic modes may develop in the current sheet with a growth rate of the order of a few tenths of a second provided that the typical scale of density gradient slope responsible for the diamagnetic drift effects is over one Earth radius or less. This instability growth rate is large enough to destabilize the current sheet on time scales of 2–4 minutes as observed during substorm onset.