Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gorshkov, Konstantin A.
and
Pelinovsky, Dmitry E.
1995.
Asymptotic theory of plane soliton self-focusing in two-dimensional wave media.
Physica D: Nonlinear Phenomena,
Vol. 85,
Issue. 4,
p.
468.
Allen, M. A.
and
Rowlands, G.
1995.
Stability of obliquely propagating plane solitons of the Zakharov–Kuznetsov equation.
Journal of Plasma Physics,
Vol. 53,
Issue. 1,
p.
63.
Bettinson, David
and
Rowlands, George
1996.
Stability of the one-dimensional kink solution to a general Cahn-Hilliard equation.
Physical Review E,
Vol. 54,
Issue. 6,
p.
6102.
Allen, M.A.
and
Rowlands, G.
1997.
On the transverse instabilities of solitary waves.
Physics Letters A,
Vol. 235,
Issue. 2,
p.
145.
Infeld, E.
and
Lenkowska-Czerwin-acuteska, T.
1997.
Analysis of stability of light beams in nonlinear photorefractive media.
Physical Review E,
Vol. 55,
Issue. 5,
p.
6101.
O'Keir, I S
and
Parkes, E J
1997.
The derivation of a modified Kadomtsev–Petviashvili equation and the stability of its solutions.
Physica Scripta,
Vol. 55,
Issue. 2,
p.
135.
Bettinson, David
and
Rowlands, George
1997.
Stability of the two- and three-dimensional kink solutions to the Cahn-Hilliard equation.
Physical Review E,
Vol. 55,
Issue. 5,
p.
5427.
Senatorski, A.
and
Infeld, E.
1998.
Breakup of two-dimensional into three-dimensional Kadomtsev-Petviashvili solitons.
Physical Review E,
Vol. 57,
Issue. 5,
p.
6050.
Bettinson, David
and
Rowlands, George
1998.
Transverse stability of the one-dimensional kink solution of the discrete Cahn-Hilliard equation.
Physical Review E,
Vol. 57,
Issue. 1,
p.
169.
Bridges, Thomas J.
2000.
Universal Geometric Condition for the Transverse Instability of Solitary Waves.
Physical Review Letters,
Vol. 84,
Issue. 12,
p.
2614.
Kivshar, Yuri S.
and
Pelinovsky, Dmitry E.
2000.
Self-focusing and transverse instabilities of solitary waves.
Physics Reports,
Vol. 331,
Issue. 4,
p.
117.
Bandyopadhyay, A
and
Das, K P
2001.
Stability of Ion-Acoustic Double Layers in a Magnetized Plasma Consisting of Warm Ions and Nonthermal Electrons.
Physica Scripta,
Vol. 63,
Issue. 2,
p.
145.
Bridges, Thomas J.
and
Reich, Sebastian
2001.
Multi-symplectic spectral discretizations for the Zakharov–Kuznetsov and shallow water equations.
Physica D: Nonlinear Phenomena,
Vol. 152-153,
Issue. ,
p.
491.
Wen-Shan, Duan
Xue-Ren, Hong
Yu-Ren, Shi
Ke-Pu, Lu
and
Jian-An, Sun
2002.
Weakly Two-Dimensional Solitary Waves on Coupled Nonlinear Transmission Lines.
Chinese Physics Letters,
Vol. 19,
Issue. 9,
p.
1231.
Blyuss, K. B.
Bridges, T. J.
and
Derks, G.
2003.
Transverse instability and its long-term development for solitary waves of the (2+1)-dimensional Boussinesq equation.
Physical Review E,
Vol. 67,
Issue. 5,
Duan, Wen-shan
2003.
Weakly two-dimensional modulated wave packet in dusty plasmas.
Physics of Plasmas,
Vol. 10,
Issue. 7,
p.
3022.
Duan, Wen-shan
2004.
Two-dimensional envelop ion acoustic wave under transverse perturbations.
Chaos, Solitons & Fractals,
Vol. 21,
Issue. 2,
p.
319.
Duan, Wen-shan
Zhang, Lei
Lin, Mai-mai
Hong, Xue-ren
and
Lv, Ke-pu
2005.
Cylindrical higher order disturbances to planar solitary waves.
Chaos, Solitons & Fractals,
Vol. 26,
Issue. 2,
p.
325.
Jorge, M. C.
Cruz-Pacheco, Gustavo
Mier-y-Teran-Romero, Luis
and
Smyth, Noel F.
2005.
Evolution of two-dimensional lump nanosolitons for the Zakharov-Kuznetsov and electromigration equations.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 15,
Issue. 3,
Das, Jayasree
Bandyopadhyay, Anup
and
Das, K. P.
2007.
Existence and stability of alternative ion-acoustic solitary wave solution of the combined MKdV-KdV-ZK equation in a magnetized nonthermal plasma consisting of warm adiabatic ions.
Physics of Plasmas,
Vol. 14,
Issue. 9,
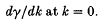 We introduce a more direct analytical method in the form of an extension to the usual multiple-scale perturbation approach and use it to determine a consistent expansion of γ about k = 0 and the other zero at k2 = 5.By combining these results in the form of a two-point Padé approximant, we obtain an analytical expression for γ valid over the entire range of k for which the solution is unstable. We also present a very efficient numerical method for determining the growth rate curve to great accuracy. The Padé approximant gives excellent agreement with the numerical results.
We introduce a more direct analytical method in the form of an extension to the usual multiple-scale perturbation approach and use it to determine a consistent expansion of γ about k = 0 and the other zero at k2 = 5.By combining these results in the form of a two-point Padé approximant, we obtain an analytical expression for γ valid over the entire range of k for which the solution is unstable. We also present a very efficient numerical method for determining the growth rate curve to great accuracy. The Padé approximant gives excellent agreement with the numerical results.