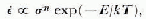Introduction
Most materials exhibit the phenomenon of creep at high temperatures. When subject to mechanical load, they continue to deform once the initial elastic response has occurred. A plot of the amount of deformation (strain) against the time since the start of the test is known as a creep curve.
Polycrystals of ice, like most metals, have initially decelerating creep curves (Fig. 1a). At moderate stresses the creep rate begins at a high value and then slowly falls, after a while reaching a constant minimum value before eventually increasing again. For low stresses the final rise in the creep rate can be absent; for high stresses the minimum value may be essentially a point of inflexion on the graph.
Monocrystals of ice, on the other hand, have creep curves which are accelerating (Fig. lb). Such an accelerating creep curve is to be expected in a material, which, as the creep test begins, has a low dislocation density. The velocity of the dislocations is low and cross-slip from one slip plane to another is difficult. Therefore, dislocations multiply by the usual

Fig. 1. a. The creep curve obtained when a polycrystal is deformed at moderate stresses.
b. The creep curve obtained when a monocrystal is deformed so that there is a resolved shear stress on the basal plane.
methods (Frank–Read sources, etc.) but few or no dislocations become immobile. Under these conditions the creep rate must increase. Such an effect is observed in other materials of a similar crystallography to that of ice. The creep rate for a monocrystal is much higher than that for a polycrystal, given the same test conditions (temperature and stress).
Polycrystals have decelerating creep curves because the interaction between grains forces the deformation process to slow down, or stop, in grains which are favourably orientated for slip. Steady-state creep is reached when the rate at which grain deformation is blocked equals the rate of grain release. Further increase in the strain-rate is due to recrystallization in the bulk of the ice, producing collections of grains which are more favourably oriented for creep and which, therefore, can develop a higher strain-rate. In the past, the minimum creep rate of any particular deforming polycrystal has been taken as an indicator of its deformation rate. This minimum creep rate has been related to the stress and temperature by the expression:
where ![]() is the minimum strain-rate, σ is the stress, n is a constant, typically about 3, E is the creep activation energy, k is Boltzmann’s constant, and T is the temperature. The use of such an expression assumes that the processes which operate the creep mechanism are thermally activated, and that all have the same activation energy.
is the minimum strain-rate, σ is the stress, n is a constant, typically about 3, E is the creep activation energy, k is Boltzmann’s constant, and T is the temperature. The use of such an expression assumes that the processes which operate the creep mechanism are thermally activated, and that all have the same activation energy.
An expression similar to (1) has been adopted for monocrystals—though with more difficulty as regards the decision as to where on the creep curve the rate should be measured. Table I contains a brief and necessarily condensed summary of previous work on both polycrystals and monocrystals. It will be seen that n is typically 3 for polycrystals and 2-3 for monocrystals, while E is in the ranges 50–70 kJ/mol for monocrystals and 40–140 kJ/mol for polycrystals. A more complete review of the present position will be found in Glen (1975).
Walker (unpublished) has noted that below — 10°C the values obtained for creep activation energies for polycrystals are much smaller than those obtained above — 10°C. He has advanced the idea that this rise in apparent activation energy is due to the appearance of liquid at the grain boundaries. This conclusion hinges on the assumption that there is no corresponding increase in the creep activation energy for monocrystals near to the melting point.
In the research reported here, we have attempted to measure the creep activation energy for monocrystals close to the melting point, and to deform ice bicrystals in order to assess the effect of a single grain boundary on creep.
Table I

Experimental Method
In order to achieve the objectives of the experiment, it was desirable to grow, and then to deform, ice bicrystals which have a single plane grain boundary running parallel to the tensile axis (Fig. 2).
These bicrystals were subsequently deformed by tensile stresses acting parallel to the plane of the grain boundary; this is a configuration which does not permit slip between the individual

Fig. 2. A diagram showing the relationship between the grain boundary and the tensile axis in the bicrystal.
grains which make up the bicrystal. In other words, a deformation test made on this type of specimen should examine the effect which a grain boundary has on slip when macroscopic grain-boundary sliding is not permitted.
Growing the bicrystals
The bicrystals were grown by a method due to Adams and Lewis (1934) which has since been extended by Roos (1975). Our technique was developed independently from that of Roos though it can be considered as essentially an extension of his ideas.
Monocrystals of ice were first produced by the method of Glen (Glen and Jones, 1967) in glass tubes of constant, square cross-section. They were frozen from water which had a conductivity of 8 × 106 Ω-1 m-1, and the freezing was carried out using well-leached glass materials. The monocrystals thus produced were square in cross-section about 100 mm long with the other cross-section 10 mm × 10 mm.
We consider two distinct types of orientation between the grains of the bicrystals:
(A) Different angles between the tensile and c-axis in the two grains.
(B) Same angle between the tensile and c-axis in both grains but a rotation of one grain relative to the other about the tensile axis.
For bicrystals in the A category, two separate monocrystals of different orientation were used as seeds; for those of type B a monocrystal was cut in half and one half was rotated by multiples of 90° relative to the other to achieve the desired misorientation. However, the same growth method was used whichever type of bicrystal was being made.
Inside a cold chamber, the two seed monocrystals were frozen side-by-side, but not in contact, on to the machined face of a brass block which had previously been cooled to — 6°C. The crystals, but not the brass, were then dipped into ice-cold water (with a similar impurity concentration to the water used in preparing the monocrystals). The water was contained in a beaker mounted on a magnetic stirring device consisting of a motor which rotates a magnet inside a base upon which the beaker may be placed. Another small magnet is placed inside the beaker and is attracted to, and rotates with, the motor-driven magnet. The motor speed was adjusted so that the heat from the motor was sufficient to maintain the water at 0°C as the whole apparatus was held in a cold room. The movement of a stirrer provided the axial rotation which is necessary in a Czochralski (or Kyropoulos) growth technique so that, in our case, the melt was rotated relative to the seed, whereas the more usual technique with other materials is to rotate the seed relative to the melt. Rather than raise the growing bicrystal from the water, we lowered the water level using a syringe. The growth of these specimens can proceed remarkably quickly, if required. We maintained our growth rates at no more than a few millimetres per hour.
This technique produces clear bubble-free ice with a straight grain boundary. With a single seed it will also produce monocrystals of high quality (when viewed through crossed polars).
The shape of the surface of the growing crystal is always convex into the water, and this tends to produce an ice with a lower impurity concentration than the water from which it is made (Bilgram, 1973). We believe, as do others, that a technique where no constraint is applied to the growing crystal can produce crystals in which the dislocation densities are initially much lower than densities found in crystals grown by methods in which there is confinement of the crystal within a tube. The original seeds of our bicrystals were, for this reason, always discarded.
From time to time, bicrystals were melted and the melt water tested for fluoride ion concentration using a specific-ion probe. The concentration of this ion, the most significant dopant for ice as far as mechanical properties are concerned, was always less than 0.1 p.p.m.
When the bicrystal or monocrystal had been produced, it was removed from the brass block and trimmed by melting and cutting with a hot-wire cutter into three or four tensile specimens of an appropriate size.
The final stage in the preparation was to “freeze-tap” each surface of the bicrystal (Tobin and Itagaki, 1970). This process is said to ensure that the ice surfaces have a low dislocation density. In any event, it produces a perfectly flat surface, which is of value later in the optical examination of a strained bicrystal.
The specimens used in the creep tests were about 25 mm long by about 5 mm square with the grain boundary running down the centre of the specimen parallel to the tensile axis.
Testing the specimens
Figure 3 shows a diagram of the creep-test machine used. It is of a compact design to operate within an available cold chamber.

Fig. 3. The creep-test machine.
The creep machine consists of two frameworks, one sliding within the other. The fixed framework is made of three threaded brass rods AA′ along which three circular Duralumin plates B are bolted. The rods pass through holes drilled 120° apart around the circumference, near the edge of the plates. A threaded brass cylinder c with a flat machined face at one end and a hook at the other is screwed into the centre of the middle plate. The moving framework also has three brass rods and three circular Duralumin plates. These rods are not threaded but are machined smooth; the plates are fixed to them by means of brass clamping collars. The middle plate carries a displacement transducer D.
The moving framework fits into the holes drilled into the upper and middle plates inside the fixed framework as shown by the dotted lines on the diagram. The spring-loaded armature of the displacement transducer touches the machined face of the threaded cylinder C. A load placed on the top moving plate acts through the framework into the hook at F. As the specimen creeps, the bottom plate and the rest of the moving framework carrying the transducer body move downwards. This changes the length of the armature within the body of the transducer which in turn governs the d.c. voltage from the device. The relative movement of the framework is thus detected, and this is the change in length of the crystal under test. Not shown on the diagram is a system of pulleys which counter-balanced the weight of the moving framework so that low loads could be applied to the test specimens.
A 12 V d.c. supply provided power for the displacement transducer. The output from the transducer was recorded in paper-tape form at regular time intervals throughout the test.
A complete test was conducted as follows: a specimen was frozen into end grips and its dimensions were measured. The specimen was fitted into the pre-cooled creep machine and, after allowing sufficient time for the ice to reach the temperature of the cold chamber, the test was begun by loading the top plate and by activating a data-logging system.
At the end of a test, marked by the fracture of a specimen or by the creep machine reaching the limit of its extension (a strain of about 0.2), the specimen was removed from the machine and examined,
Results
In all, 32 monocrystals and 255 bicrystals were tested at stress levels which ranged between 0.1 and 2 MN m -2, and at the four temperatures —4.5, —10, —15, and — 20°C.
Monocrystals
All the monocrystals had an angle of 45° between the optic and tensile axes. The data of strain against time for each test were fitted to the equation:
where ϵ is the strain, t is the time since the start of the test, A and B are constants, and m is an exponent assumed to be constant for a particular test, the mean value of which was found to be 1.9 ± 0.5.
The assumption of constant m is not strictly true. Logarithmic plots of the creep curves have gradients (and hence values for m) which increase as the strain increases sometimes rising to a value as high as 5. This increase began to occur after a strain of 0.01 had been passed. Steinemann (1954) and Jones (unpublished) also noted a change in the value of m at a strain level of about 0.01. Rotation of the optic axis relative to the tensile axis will produce changes in the resolved shear stress acting on the basal plane and could be responsible for a change in m.
The definition of an appropriate strain-rate to characterize a monocrystalline creep rate is difficult. Some workers have used the minimum creep rate in the same way that one might for a polycrystal test. This is undesirable, as it leads to creep rates being determined at the start of the test when effects due to starting the test will still be in evidence.
Another method which has been used is to evaluate
As ϵ
![]() t
m
and
t
m
and ![]() t
m-l, such an expression should be constant for a particular test; however, we felt that our values for m varied too much to allow a single value to be used, and if the value of m peculiar to a particular test is used in the analysis of that test then one is comparing a series of numbers which have effectively different dimensions. Accordingly, we used the creep rates for each test at three particular strains: 0.01, 0.05, and 0.10. These were obtained from a simple computer analysis of the data.
t
m-l, such an expression should be constant for a particular test; however, we felt that our values for m varied too much to allow a single value to be used, and if the value of m peculiar to a particular test is used in the analysis of that test then one is comparing a series of numbers which have effectively different dimensions. Accordingly, we used the creep rates for each test at three particular strains: 0.01, 0.05, and 0.10. These were obtained from a simple computer analysis of the data.
The advantage of evaluating strain-rates at a constant strain is that the rate is obtained at three separate microstructures (assuming that the dislocation density is a function of strain only) and at approximately the same specimen shape.

Fig. 4. Three plots of ![]() versus a for monocrystals. The strain-rates were derived at a strain of 0.05.
versus a for monocrystals. The strain-rates were derived at a strain of 0.05.
A plot of log ![]() (at a strain of 0.05) against log σ is shown, by way of example, in Figure 4. A mean value of 1.9(5) ± 0.1 (4) was found for the constant n in the expression
(at a strain of 0.05) against log σ is shown, by way of example, in Figure 4. A mean value of 1.9(5) ± 0.1 (4) was found for the constant n in the expression
This mean value for n was obtained from eight such graphs. The individual gradients of the graphs (i.e. n) are shown in Table II.
The activation energy obtained graphically from the data was 78 ± 4 kJ/mol.
Table II. Values of the Stress Exponent n for Monocrystals Determined from the log–log Graphs of Strain-Rate plotted Against Stress

Temperature Strain level°C0.010.050.1— 4.51.81.7(2)*— 10.01.912.12.1— 20.02.02.02.0
* Data were insufficient to determine an accurate value here; few monocrystals crept 0.10 before fracturing. The strain-rates become very large indeed.
Bicrystals
The bicrystals were tested at six different temperatures: — 4.5, — 10, — 15, — 20, and —30°C.
When type A specimens were deformed in creep, it was found that the creep rate of the bicrystal was governed by the grain with the lower resolved shear stress on the basal plane. This is not surprising and was very obvious when an extreme misorientation was used, such as 10° and 45°. In such a case, many small slip lines would develop on the surface of the grain which had the smaller resolved shear stress, whereas on the surface of the grain with the greater resolved shear stress there were a few poorly developed slip lines.
Most creep tests were carried out with type B bicrystals, that is, specimens with identical angles between optic and tensile axes in both grains, but with a rotational misorientation between the grains. The angle between the optic and tensile axes was chosen to be 45°.
When type B bicrystals were deformed, slip lines were again visible on the surface of the ice. These are also a common and obvious feature of monocrystal tests and have been observed on deformed polycrystal grains (Gold, 1963). The bicrystal slip lines were, in general, much finer and more numerous than those seen on a monocrystal. There was no sign of cross-slip or waviness in the slip lines near to the boundary even under optical microscopic examination. Indeed, when there was a misorientation, the two sets of slip lines clearly delineated the grain boundary which is not normally visible, except when the ice is viewed through crossed polarizing filters.
Sometimes the bicrystals fractured in the centre of the specimen. This is unusual for a tensile creep test of this type. The stress concentrations at the end grip are such that the crystal might be expected to fracture there. When a bicrystal fractured centrally, the fracture was often associated with small internal cracks close to or on the grain boundary. Some bicrystals

Fig. 5. Typical bicrystal creep curves.
which did not fracture during test were also observed to have these small cracks after the test when removed from the test apparatus.
Neither grain growth nor recrystallization were observed in the bicrystal tests (grain growth is here taken to mean the development of one grain at the expense of the other; recrystallization is the nucleation of a new grain of orientation different from the others in the specimen).
Such a lack of structural alteration is probably to be expected. Both halves of the bicrystal have the same angle between the optic and tensile axes and so neither is more favourably oriented for growth than the other. At larger strains, as rotation of the basal planes occurs, sufficient strain energy may be stored at the grain boundary to trigger a recrystallization.
Typical bicrystal creep curves are shown in Figure 5. They are accelerating in character. Logarithmic plots of strain against time indicate that the exponent m in Equation (2) is 1.3±0.4. The analysis of the type B bicrystal creep results was similar to the monocrystal analysis. Creep rates were determined at strain-rates of 0.01, 0.05, 0.1 and in addition the value ![]() was derived for each creep test. These derived data were plotted against stress for a constant temperature and strain level. Bicrystal creep rates are roughly a factor often lower than equivalent monocrystal rates. There is no apparent dependence of the creep rate or the exponent m on the degree of misorientation,
was derived for each creep test. These derived data were plotted against stress for a constant temperature and strain level. Bicrystal creep rates are roughly a factor often lower than equivalent monocrystal rates. There is no apparent dependence of the creep rate or the exponent m on the degree of misorientation,
Again, following the monocrystal analysis, the relationship between strain-rate and stress (expression (3)) indicated that
Table III shows the individual values of n obtained for each temperature–strain level. The creep activation energy for the bicrystals was 75±2 kJ/mol.
Table III. Values of the Stress Exponent n for Bicrystals Determined from the Graphs of Strain-Rate Against Stress and ![]() Against Stress
Against Stress

Discussion
Monocrystals
The mechanical properties of the monocrystals reported here are similar to those of previous workers. The activation energies here are somewhat greater than previous values but by less than 10%, and the stress exponent n was 1.9, falling well within the range of values observed by other investigators. There was considerable spread in the four values for the activation energy. This is especially noticeable at the 0.01 strain level and denies our assumption concerning the possible initial behaviour at the start of a monocrystal creep test (which was that at a strain of 0.01 any atypical behaviour due to the initial state of specimen should have been eliminated). By the time the crystal has strained by 0.05 the creep specimens are apparently showing much more uniform behaviour. ‘The question arises whether the 10% higher activation energy given by the tests as compared with the results of other workers can be explained as being due to the methods used for specimen preparation. Muguruma (1969) showed that in constant strain-rate tests the values of the activation energy and the stress exponent depend on the method used for the preparation of the ice. His results would imply that the ice in this study had a high surface dislocation density. This is however unlikely, because the Itagaki “freeze-tap” method has been shown to produce a strain-free surface with a low dislocation density (Tobin and Itagaki, 1970), in fact, a better surface than can be obtained by using a fracture surface (Tobin, 1973). The fact that the crystal was unconfined during growth should also result in a low dislocation density in the ice; it is therefore necessary to look elsewhere for reasons for the activation energy increases.
Most of the creep experiments undertaken previously were at somewhat lower temperatures than those presented here. Higashi’s experiments were in the range — 15 to — 40°C; those of Jones were mostly below about — 50°C. It seems probable that the activation energy increase observed here is a genuine one, and that the results show a true rise in the activation energy for monocrystalline creep as the temperature rises. We shall see later that there is independent evidence to support this.
Weertman (1973) has pointed out that, at present, the three-regime model of Barnes and others (1971) can be no more than a hypothesis simply because no adequate investigations of monocrystalline creep have been made at temperatures near to the melting point. This was the justification for carrying out monocrystalline creep tests here. It will be recalled that the work of Walker hinged on his observation of a gross increase in the activation energy for polycrystalline creep from 78 to 120 kJ/mol between — 10°C and the melting point.
Our experiments do not reveal a similar gross increase in monocrystals or bicrystals and thus confirm Walker’s view that the large increase in activation energy in poly crystals is due to causes other than those of intra-granular activity. There does, however, appear to be a small general rise in the energy value throughout the range of temperatures for which tests have been reported (from — 90°C upwards). This is also apparent in Walker’s own polycrystalline data.
The activation energies derived in Walker’s and most other ice experiments are only apparent activation energies. In general, the temperature dependence of the elastic modulus has been neglected in the analysis and derivation of the true strain-rate. For metallurgical work, the constitutive relation:
is often re-written as:
where D is the diffusion coefficient, Ω is the atomic volume, E T is the elastic modulus, and A ′ is a constant (Weertman, 1973). Both D and E T are temperature dependent:
and
where α is a constant and θ is the temperature difference between the temperature T and the melting point in kelvins.
As Ramseier (unpublished) has pointed out, the modulus effect is significant in polycrystalline ice, but not in monocrystalline material as α for a monocrystal is very small (Gold, 1958). If Walker’s data are corrected for the modulus changes, the activation energies become true rather than apparent, and by taking strain-rates at an effectively constant stress for calculating the activation energies the diffusion-coefficient compensation becomes irrelevant so that the diffusion-controlled creep assumption is not made. The corrected activation energies are given in Table IV in which the activation energy is seen to be increasing as the temperature rises. It is also worth noting that Steinemann (1958) found an apparent activation energy of about 82 kJ/mol in this temperature range (when his data are analysed using Walker’s data-reduction techniques). This corresponds to a true activation energy of about 68 kJ/mol. The activation energies derived by Steinemann and Walker are similar to those corrected activation energies derived from the present work at temperatures between — 8 and — 20°C. (The effect of the correction for the results presented here is to reduce them by 3 kJ/mol.) At lower temperatures, Walker’s energies are similar to those obtained from mono-crystal tests at equivalent temperatures. Thus, the results presented here confirm that there is no large and almost discontinuous change in the activation energy of monocrystals near to the melting point. On the contrary, the activation energy for monocrystalline creep is monotonically increasing from the lowest temperatures at which creep has been detected. Further, the true activation energy for polycrystalline creep at medium temperatures is almost identical to the activation energy for monocrystalline creep, thus providing more evidence for Walker’s model. In their paper, Barnes and others (1971) assumed that the activation energy for monocrystalline creep is nearer the values for self-diffusion and dielectric relaxation than our analysis here would indicate.
Table IV. Walker’s Activation Energies for Polycrystalline Creep with a Correction for the Elastic Modulus Effect (After Barnes and Others, 1971)

Temperature range Uncorrected activation energy Corrected activation energy°CkJ mol-1kJ mol-1— 8 to — 1478.664.7— 14 to — 2278.863.3— 22 to — 3476.462. 1
The position is, of course, not so straightforward as this. There are at least two extensive and well-founded studies which have produced a lower monocrystal creep activation energy than the experiments considered here. Both Ramseier (unpublished) and Readey and Kingery (1964) have derived energies from constant strain-rate tests which are identical to the activation energy for self-diffusion in monocrystals. There is, however, some evidence to suggest that tins value only obtains in the higher stress range above perhaps 2 MN/m2. If the data of Ramseier (unpublished) are re-plotted as strain-rate against stress at a constant temperature, it becomes clear that the activation energy is stress-dependent. At high stresses, therefore, the value of the activation energy is indeed 59.5 kJ/mol but at lower stresses (less than 2 MN/m2) it seems likely that it is higher. We have obtained a value for Ramseier’s activation energy of 65 kJ/mol at a stress of 0.1 MN/m2 in the temperature range — 10 to — 30°C (his data were obtained at three separate temperatures). 2 MN/m2 is also the stress at which a change occurs in the relationship between the stress and the strain-rate. Above 2 MN/m2 (Ramseier, unpublished):
whereas below 2 MN/m2
Thus two separate mechanisms are indicated for monocrystals. Above 2 MN/m2, a stress level more likely to be found in constant strain-rate or compressive creep tests, the strain-rate is proportional to stress raised to the power 2.5 and the activation energy is about 60 kJ/mol; below 2 MN/m2, the strain-rate is proportional to the square of the stress and the activation energy (at the lowest stresses and highest temperatures) is 75 kJ/mol. There is some evidence to suggest that at lower temperatures, down to perhaps — 80°C, the stress-transition level falls so that in tests at these temperatures all practicable strain-rates are produced by stresses greater than the transition level.
The mechanisms which operate in these two regimes are of some interest; as we are dealing with monocrystals, it seems certain that basal slip is operating in both cases. At least the literature contains no reports of non-basal deformation in monocrystals in any tests in which appreciable resolved shear stress operates upon the basal plane.
At higher stresses the activation energy is close to the values obtaining in dielectric and anelastic relaxation processes. It seems that the mechanism involved in all three processes is the re-orientation of protons around individual water molecules by the movement of Bjerrum defects. Therefore, this same process may control the deformation of monocrystals at the higher stresses. Essentially, this is the same suggestion as that made by Glen (1968).
Bicrystals
The type B bicrystals had creep curves which were accelerating, yielding a similar activation energy to those of monocrystals and polycrystals, and showed a relationship between strain-rate and stress which closely resembles that of a polycrystal. Bicrystal creep rates were slower than those of monocrystals by roughly an order of magnitude for similar lest conditions.
Monocrystals are free to deform by slip upon their basal planes providing that there is some resolved shear stress acting on these planes. Our type B bicrystals are two monocrystals with the same orientation relative to the tensile axis, joined by a grain boundary along one lace o each crystal, which does not impose very great constraint to slip deformation on the basal planes. Our experiments illustrate the effect of this single boundary on the creep of the bicrystal.
There was within experimental error, no difference between the possible types of misorientation which were examined. The grain boundary imposes constraints on dislocation movement even when the Burgers vector is parallel to the grain boundary in both grains (Fig. 6). The interaction of a dislocation with a boundary is more obvious when a dislocation, whose Burgers vector is perpendicular to the grain boundary, moves up to it.
A frequent observation was that a large number of slip lines appeared on the surface of bicrystals compared to the relatively small number which appeared on the surface of a monocrystal deformed by the same amount.
Thus there are more dislocation sources operating in each grain of a bicrystal than there would have been in an equivalent monocrystal, and these increased numbers of sources are operating more slowly.

Fig. 6. Two possible grain-boundary arrangements which were examined.
a. basal planes crossed; Burgers vectors parallel to boundary.
b. basal planes meeting; Burgers vectors perpendicular to boundary.
It is possible that the bicrystal growth method may have resulted in a higher initial dislocation density compared with the monocrystals but, as a similar method was used to grow the monocrystals, this seems unlikely.
A more plausible explanation for the increase in the number of dislocations is that they are generated at the boundary. It seems certain that with the high degree of disorder which is found at a boundary, mobile dislocations can be produced here initially and can then cross slip or jog to produce an active Frank–Read source. This may then operate in the usual way to generate more dislocations.
It is also possible that the constraints imposed by the boundary produce a back stress on the most active sources within the crystal and allow further sources to operate.
Despite the increased number of sources, our bicrystal creep rates are lower than those for monocrystals; many basal systems are operating but the overall strain-rate is lower. The mobile dislocation density must therefore be lower if the dislocation velocity is constant and the strain-rate is reduced. No large-scale boundary migration took place, and no step structure formed at the boundary. Either few dislocations with Burgers vectors perpendicular to the boundary only are able to move up the slip planes into the grain boundary, or the boundary is able to absorb large numbers of dislocations without displacement.
The former possibility is the more likely as the steps on the crystal surface were so small, implying only a limited freedom for the dislocations.
Thus, the grain boundary in the bicrystals does not affect the process by which the ice deforms (slip by dislocation movement on basal planes); the boundary acts to slow down the deformation rate. The unchanged activation energy is evidence for this.
Polycrystalline deformation
The creep mechanism at the molecular scale for monocrystal deformation at low stresses is not well understood. One of the existing theories, due to Glen (1968) has recently been made more quantitative by its author and others (Whitworth and others, 1976), and this has shown it to be inadequate at present to explain the observed rates. However, deformation in mono-crystals is certainly due to basal-plane processes, with only small contributions from other sources. We have suggested that, except at very high temperatures, the activation energies for creep in monocrystals, bicrystals, and polycrystals are closer than had previously been thought. There is thus the strong possibility that the controlling processes are the same in all types of creep. In other words, the rate-limiting mechanism would seem to be that controlling the glide of dislocations across the basal plane.
It is clear, of course, that polycrystals differ from monocrystals in a rather marked way. All grains in the polycrystal are bounded by other grains except at the surface. We have shown that the presence of only one grain limits the freedom of the basal slip systems to operate. Grains surrounded on all sides are still less free to deform. Any slip must result in the creation of a step at a boundary.
The first two stages may be described in the following way:
(1) Primary creep
Here there is an increasing interaction between the dislocations and the grain boundary. This takes the form of a piling-up of dislocations at grain-boundary barriers, a process which takes longer in some grains than others due to the differences in resolved shear stresses on the basal plane from grain to grain. The creep rate slows down because fewer and fewer grains are left operating.
(2) Secondary creep
Eventually the secondary region of creep is reached; here a steady-state condition obtains in which the rate of release of blocked dislocations equals the rate at which other operating sources are blocked. It is possible that stress concentrations arising from intra-granular interactions induce the operation of non-basal slip systems; systems which normally have yield stresses (in constant strain-rate tests) of the order of 1 MN m-2, a factor of ten greater than the yield stresses of basal systems. Near to the melting point, grain-boundary sliding and the observed thermodynamic grain-boundary liquid (Nye and Mae, 1972) also play a part. All these interactions proceed at different rates in different grains and are, in general, slower in all grains than might at first be expected. There are two reasons for this. First, most types of polycrystalline ice have some degree of misalignment between the grains and between the tensile axis and any particular grain. Thus, when the ice is stressed there are varying resolved shear stresses acting on the basal plane’s Sources must therefore operate at different speeds. Also, ice has only two independent slip systems on the basal planes and Weertman (1968) has shown (we have altered his calculation slightly (Homer, unpublished)) that from geometrical considerations alone, one would expect the expression

where k is a constant associated with the creep of a monocrystal. A creep reduction factor of 25 is expected for randomly orientated ice. If all these factors are taken into account, then it is possible to account for the whole of the ratio difference of about 1 000 in the creep rates of polycrystals and monocrystals.
Acknowledgements
We thank Mr J. H. Emery for much technical assistance, and Dr J. G. Paren and Dr R. W. Whitworth for their advice. One of us (D.R.H.) is grateful to the Natural Environment Research Council for a Research Studentship.
Discussion
T. O’D. HANLEY: The power-function relation between strain-rate and stress,
is purely empirical; the relation of the exponent n to such parameters as activation energy and activation volume has been investigated, but it is complicated. Would it not be more informative to employ an equation based on a well-established model, an equation whose parameters have a clear and simple meaning? Hanley and Krausz (1974) have published a good fit to such a model over several orders of magnitude of stress relaxation in ice, and are currently working on a model for creep and for tests at constant strain-rate in ice, expressed by an equation of the following form:
where M is a factor to account for multiplication of dislocations, H is a factor for strain hardening, and the other quantities need not be explained in this brief note.
D. R. HOMER: I agree. One clearly wishes to know the mechanism which is at work. However, from the point of view of comparison between authors, one evaluates activation energies and exponents in order to say X obtained this value, Y obtained that.
J. W. GLEN: It is not quite true to say that the power-law relation is purely empirical. Although it was first suggested empirically, Weertman (1957[a], [b], 1963) subsequently elaborated a theory of creep based on dislocation climb that resulted in a power law.
T. HONDOH: In your bicrystal specimens, what are the crystallographic indices of the rotation axes? What about thickness?
HOMER: When the bicrystals are grown, the water is rotated about an axis which is at 90° to the eventual tensile axis of the specimen. The dimensions of the specimens were approximately 5 mm square by 25 mm long.
D. TABOR: It is naturally very gratifying to find that one’s earlier work is supported by the elegant experiments described by Homer and Glen. I would like to ask one question. The creep rate with the bicrystal is ten to one hundred times smaller than with the monocrystal. Do the authors feel that it is fair to attribute the creep in both cases to a single mechanism?
HOMER: Yes, we believe that the reduction in the creep rate is due to processes of dislocation interaction arising because of the grain boundary. A further reduction occurs when we move from bicrystals to poly crystals; there are more interactions as there are more grain boundaries.