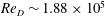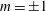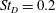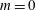1 Introduction
At low Reynolds numbers, many flows are able to sustain a stable stationary state when perturbed. With increasing Reynolds number, such flows may undergo a change in stability that affects the whole flow field and become globally unstable. This change in stability is termed a bifurcation, with Reynolds number being the bifurcation parameter. Flows which exhibit a global instability are known as oscillator flows, and bluff-body wake flows are an example (Huerre & Monkewitz Reference Huerre and Monkewitz1990; Chomaz Reference Chomaz2005).
In the simple case of the flow behind a cylinder, an unstable oscillatory global mode exists above
![]() $Re_{c}=46$
due to a supercritical Hopf bifurcation which gives rise to periodic vortex shedding (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987). The evolution of the amplitude of the global mode with time, starting from the exponential growth characterised by linear instability, and progressing to the nonlinear saturation characterised by a stable limit cycle, can be modelled using the Stuart–Landau equation. This weakly nonlinear model can be derived from the Navier–Stokes equations, by considering asymptotic expansions close to the threshold of the bifurcation (Sipp & Lebedev Reference Sipp and Lebedev2007).
$Re_{c}=46$
due to a supercritical Hopf bifurcation which gives rise to periodic vortex shedding (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987). The evolution of the amplitude of the global mode with time, starting from the exponential growth characterised by linear instability, and progressing to the nonlinear saturation characterised by a stable limit cycle, can be modelled using the Stuart–Landau equation. This weakly nonlinear model can be derived from the Navier–Stokes equations, by considering asymptotic expansions close to the threshold of the bifurcation (Sipp & Lebedev Reference Sipp and Lebedev2007).
The Stuart–Landau equation has been widely used to predict the oscillation amplitude and frequency of flows undergoing a supercritical Hopf bifurcation. Sipp (Reference Sipp2012) extended the weakly nonlinear analysis in the case where open-loop forcing is applied externally to the system and accurately captured the evolution of the forced global instability in the laminar cavity flow. Multiple coupled Landau-like equations have been also shown to apply to more complicated flows in which several linearly unstable modes interact. These include axisymmetric bluff bodies such as the disk and the sphere (Fabre, Auguste & Magnaudet Reference Fabre, Auguste and Magnaudet2008; Meliga, Chomaz & Sipp Reference Meliga, Chomaz and Sipp2009). Thus far, weakly nonlinear modelling of bluff-body flows has been limited to laminar, low Reynolds number flows close to criticality.
The focus of this paper is the forced dynamics of the turbulent wake flow behind a three-dimensional axisymmetric bluff-body, characterised via wind tunnel experiments at a diameter Reynolds number of
![]() ${\sim}1.88\times 10^{5}$
. The main contributions of this paper are twofold. Firstly, we show how a weakly nonlinear analysis applied to the Navier–Stokes equations yields coupled Landau-like equations for the evolution of the dominant global modes in the turbulent regime. The effect of external forcing is also included in the equations. Similar models are known to apply to laminar flows, but we believe this is the first work demonstrating that they also apply to the dynamics of turbulent flows. Secondly, we show how the unknown coefficients of the governing Landau equations can be extracted from experiments, and we validate the derived models by predicting the effect of zero-net-mass-flux forcing on the turbulent bluff-body flow.
${\sim}1.88\times 10^{5}$
. The main contributions of this paper are twofold. Firstly, we show how a weakly nonlinear analysis applied to the Navier–Stokes equations yields coupled Landau-like equations for the evolution of the dominant global modes in the turbulent regime. The effect of external forcing is also included in the equations. Similar models are known to apply to laminar flows, but we believe this is the first work demonstrating that they also apply to the dynamics of turbulent flows. Secondly, we show how the unknown coefficients of the governing Landau equations can be extracted from experiments, and we validate the derived models by predicting the effect of zero-net-mass-flux forcing on the turbulent bluff-body flow.
The paper is organised as follows. First, in § 2 we present some relevant background both on low-dimensional modelling and on axisymmetric bluff-body flows. In § 3 we present the experimental set-up of the turbulent bluff-body flow and in § 4 some key measurements from the unforced and forced flows that justify the theoretical modelling approach. In § 5 we present the theoretical framework, deriving equations for the evolution of the dominant modes, and show how unknown coefficients in these equations can be obtained from experiments. We validate the resulting equations using experiments of the forced response of the above turbulent bluff-body flow. Finally, § 6 discusses the implications of the work.
2 Background
Key dynamics of turbulent flows, which span a high-dimensional space, may frequently be captured accurately and efficiently by projection onto a low-dimensional space. To enhance understanding of why this is the case, we begin with the governing equations, taken to be the incompressible Navier–Stokes equations:
One can expand the solution of (2.1) as an infinite sum of basis functions
![]() $\unicode[STIX]{x1D713}_{n}(\boldsymbol{x})$
that satisfy the boundary conditions, each with temporal amplitude
$\unicode[STIX]{x1D713}_{n}(\boldsymbol{x})$
that satisfy the boundary conditions, each with temporal amplitude
![]() $A_{n}$
. The solution the can be written as:
$A_{n}$
. The solution the can be written as:
Upon substitution in (2.1), a set of ordinary differential equations for the amplitudes
![]() $A_{n}$
is obtained. Quite generally, this can be written as
$A_{n}$
is obtained. Quite generally, this can be written as
where
![]() $L$
is a linear operator and
$L$
is a linear operator and
![]() $N$
is the nonlinear part. Note that this is an infinite-dimensional description, while experimental evidence suggests that many flows, including the flows behind bluff bodies, are dominated by a small number of modes. For small deviations from the steady state, the nonlinear part can be neglected. In a stable stationary state all the modes are stable in the sense that perturbations off the stationary equilibrium decay in time. Then stability implies that all the eigenvalues
$N$
is the nonlinear part. Note that this is an infinite-dimensional description, while experimental evidence suggests that many flows, including the flows behind bluff bodies, are dominated by a small number of modes. For small deviations from the steady state, the nonlinear part can be neglected. In a stable stationary state all the modes are stable in the sense that perturbations off the stationary equilibrium decay in time. Then stability implies that all the eigenvalues
![]() $\unicode[STIX]{x1D706}_{i}$
of the linear operator
$\unicode[STIX]{x1D706}_{i}$
of the linear operator
![]() $L$
are lying in the left half-complex plane (negative real part), since any solution of a linear equation can be expanded in eigenmodes whose time dependence is
$L$
are lying in the left half-complex plane (negative real part), since any solution of a linear equation can be expanded in eigenmodes whose time dependence is
![]() $\text{e}^{\unicode[STIX]{x1D706}t}$
. A mode becomes unstable if it is associated with an eigenvalue that crosses the imaginary axis gaining a positive real part. When the Reynolds number is increased, at a critical value it often happens that at least one eigenvalue crosses the imaginary axis. Whenever this situation occurs, the dynamics can be effectively reduced to a set of differential equations, where the number of variables involved is determined by the number of the unstable modes (Crawford & Knobloch Reference Crawford and Knobloch1991). Intuitively, the reason for this reduction is simple separation of time scales. Modes that have just crossed the imaginary axis have a small real part and are evolving on long time scales. All the other fast modes rapidly adapt themselves to the slow modes (Procaccia Reference Procaccia1988).
$\text{e}^{\unicode[STIX]{x1D706}t}$
. A mode becomes unstable if it is associated with an eigenvalue that crosses the imaginary axis gaining a positive real part. When the Reynolds number is increased, at a critical value it often happens that at least one eigenvalue crosses the imaginary axis. Whenever this situation occurs, the dynamics can be effectively reduced to a set of differential equations, where the number of variables involved is determined by the number of the unstable modes (Crawford & Knobloch Reference Crawford and Knobloch1991). Intuitively, the reason for this reduction is simple separation of time scales. Modes that have just crossed the imaginary axis have a small real part and are evolving on long time scales. All the other fast modes rapidly adapt themselves to the slow modes (Procaccia Reference Procaccia1988).
2.1 Dynamics and modelling of axisymmetric bluff-body flows
Several works have previously considered the investigation of the dynamics of bluff-body flows and more recently, the low-dimensional dynamic modelling of these flows. Here we focus on wakes generated by three-dimensional axisymmetric bluff bodies. At low Reynolds numbers, which are in excess of the critical Reynolds number but nonetheless correspond to laminar flow, the axisymmetric wake exhibits global modes with azimuthal number
![]() $|m|=1$
. After an initial steady bifurcation to a stationary
$|m|=1$
. After an initial steady bifurcation to a stationary
![]() $|m|=1$
mode, a second unsteady bifurcation to oscillatory
$|m|=1$
mode, a second unsteady bifurcation to oscillatory
![]() $m=\pm 1$
modes occurs giving rise to periodic vortex shedding (Bohorquez et al.
Reference Bohorquez, Sanmiguel-Rojas, Sevilla, Jiménez-González and Martínez-Bazán2011; Bury & Jardin Reference Bury and Jardin2012).
$m=\pm 1$
modes occurs giving rise to periodic vortex shedding (Bohorquez et al.
Reference Bohorquez, Sanmiguel-Rojas, Sevilla, Jiménez-González and Martínez-Bazán2011; Bury & Jardin Reference Bury and Jardin2012).
Close to the threshold of bifurcations, simple nonlinear models have been proposed that accurately capture the dynamics of axisymmetric bluff-body wakes. As mentioned above, the infinite-dimensional fluid system can be reduced to a system of ordinary differential equations governing their amplitudes when the leading destabilising global modes are simultaneously nearly neutral. Under this framework, Fabre et al. (Reference Fabre, Auguste and Magnaudet2008), using the symmetry group
![]() $O(2)$
of the problem, derived the normal form truncated at third order which describes the interaction of the three global modes (steady
$O(2)$
of the problem, derived the normal form truncated at third order which describes the interaction of the three global modes (steady
![]() $m=1$
, unsteady
$m=1$
, unsteady
![]() $m=\pm 1$
) in the wake of a sphere and a disk. Meliga et al. (Reference Meliga, Chomaz and Sipp2009) used a multiple time scale expansion to compute analytically the leading-order equations that describe the nonlinear interaction of the three leading eigenmodes in the wake of a disk. The normal form, which was the same to the normal form proposed by Fabre et al. (Reference Fabre, Auguste and Magnaudet2008), accurately predicted the sequence of bifurcations, the associated thresholds and symmetry properties observed in the direct numerical simulations.
$m=\pm 1$
) in the wake of a sphere and a disk. Meliga et al. (Reference Meliga, Chomaz and Sipp2009) used a multiple time scale expansion to compute analytically the leading-order equations that describe the nonlinear interaction of the three leading eigenmodes in the wake of a disk. The normal form, which was the same to the normal form proposed by Fabre et al. (Reference Fabre, Auguste and Magnaudet2008), accurately predicted the sequence of bifurcations, the associated thresholds and symmetry properties observed in the direct numerical simulations.
For the laminar weakly nonlinear analysis, the velocity and the pressure
![]() $\boldsymbol{q}=(\boldsymbol{u},p)^{\text{T}}$
of the Navier–Stokes equations are expanded considering the following asymptotic expansion:
$\boldsymbol{q}=(\boldsymbol{u},p)^{\text{T}}$
of the Navier–Stokes equations are expanded considering the following asymptotic expansion:
Based on the multiple-scale method used here, a ‘fast’ time scale
![]() $t$
and a ‘slow’ one
$t$
and a ‘slow’ one
![]() $t_{1}=\unicode[STIX]{x1D700}t$
, where
$t_{1}=\unicode[STIX]{x1D700}t$
, where
![]() $\unicode[STIX]{x1D700}\ll 1$
, have been introduced. The Reynolds number is defined based on the diameter of the body and the free-stream velocity,
$\unicode[STIX]{x1D700}\ll 1$
, have been introduced. The Reynolds number is defined based on the diameter of the body and the free-stream velocity,
![]() $Re=U_{\infty }D/\unicode[STIX]{x1D708}$
. Introducing (2.4) into (2.1) and considering departure of order
$Re=U_{\infty }D/\unicode[STIX]{x1D708}$
. Introducing (2.4) into (2.1) and considering departure of order
![]() $\unicode[STIX]{x1D700}$
from criticality,
$\unicode[STIX]{x1D700}$
from criticality,
![]() $Re^{-1}=Re_{c}^{-1}-\unicode[STIX]{x1D700}$
, a series of equations is obtained at various orders equating coefficients of the
$Re^{-1}=Re_{c}^{-1}-\unicode[STIX]{x1D700}$
, a series of equations is obtained at various orders equating coefficients of the
![]() $n$
th power of
$n$
th power of
![]() $\sqrt{\unicode[STIX]{x1D700}}$
to zero. At third order, compatibility equations are imposed to cancel secular terms which yield coupled Landau-like equations that describe the amplitude evolution of the linearly unstable global modes (Sipp & Lebedev Reference Sipp and Lebedev2007; Meliga et al.
Reference Meliga, Chomaz and Sipp2009).
$\sqrt{\unicode[STIX]{x1D700}}$
to zero. At third order, compatibility equations are imposed to cancel secular terms which yield coupled Landau-like equations that describe the amplitude evolution of the linearly unstable global modes (Sipp & Lebedev Reference Sipp and Lebedev2007; Meliga et al.
Reference Meliga, Chomaz and Sipp2009).
Based on the above, before reaching a highly turbulent condition, bluff-body wakes pass through a transitional state in which the time dependence of their state variables is already erratic but only a few modes are appreciably excited. Such a system can be successfully described by mathematical models involving a finite, and even small, number of dynamic variables. Recently it has been shown that the global modes appearing close to the bifurcation thresholds persist at even high Reynolds numbers and manifest as coherent structures. These modes, which are reminiscent of the temporal and spatial symmetry break mechanisms of the transitional regime, contain most of the dynamic behaviour observed in the near turbulent wake of axisymmetric three-dimensional bluff bodies (Rigas et al. Reference Rigas, Oxlade, Morgans and Morrison2014; Grandemange, Gohlke & Cadot Reference Grandemange, Gohlke and Cadot2014; Rigas et al. Reference Rigas, Morgans, Brackston and Morrison2015; Gentile et al. Reference Gentile, Schrijer, Van Oudheusden and Scarano2016). Similar behaviour has been observed for rectilinear three-dimensional bodies, such as the Ahmed body (Grandemange, Cadot & Gohlke Reference Grandemange, Cadot and Gohlke2012; Grandemange, Gohlke & Cadot Reference Grandemange, Gohlke and Cadot2013; Volpe, Devinant & Kourta Reference Volpe, Devinant and Kourta2015).
In summary, the evolution of laminar global modes in the transitional regime can be captured using simple weakly nonlinear Landau-like models. These global modes persist at high Reynolds numbers and manifest as coherent structures. In this study we will extend the weakly nonlinear analysis to the turbulent regime and validate the theoretical predictions with experimental measurements.
3 Experimental set-up
The focus of the present work is the turbulent flow around an axisymmetric bluff body with a blunt trailing edge, shown schematically in figure 1 (Rigas et al.
Reference Rigas, Oxlade, Morgans and Morrison2014, Reference Rigas, Morgans, Brackston and Morrison2015; Oxlade et al.
Reference Oxlade, Morrison, Qubain and Rigas2015). Experiments were performed in a closed circuit wind tunnel, the working section of which measures
![]() $0.91~\text{m}\times 0.91~\text{m}\times 4.8~\text{m}$
. The contraction ratio is
$0.91~\text{m}\times 0.91~\text{m}\times 4.8~\text{m}$
. The contraction ratio is
![]() $9:1$
and the free-stream turbulence intensity is less than
$9:1$
and the free-stream turbulence intensity is less than
![]() $0.1\,\%$
. A proportional–integral–derivative controller with a set-point variation of less than
$0.1\,\%$
. A proportional–integral–derivative controller with a set-point variation of less than
![]() $0.2\,\%$
was used to maintain the free-stream velocity,
$0.2\,\%$
was used to maintain the free-stream velocity,
![]() $U_{\infty }=15~\text{m s}^{-1}$
.
$U_{\infty }=15~\text{m s}^{-1}$
.

Figure 1. Schematic of axisymmetric bluff body: (a) side view; (b) rear view.
The model diameter,
![]() $D$
, is 196.5 mm and the length-to-diameter ratio,
$D$
, is 196.5 mm and the length-to-diameter ratio,
![]() $L/D$
, is 6.48. The nose employs a modified super ellipse profile with an aspect ratio of 2.5. The boundary layer was conditioned with a 2 mm wide strip of 120 grit emery paper located at
$L/D$
, is 6.48. The nose employs a modified super ellipse profile with an aspect ratio of 2.5. The boundary layer was conditioned with a 2 mm wide strip of 120 grit emery paper located at
![]() $x/L=0.884$
(approximately the point of minimum pressure). The Reynolds number based on diameter and free-stream velocity is
$x/L=0.884$
(approximately the point of minimum pressure). The Reynolds number based on diameter and free-stream velocity is
![]() $1.88\times 10^{5}$
, and at separation is
$1.88\times 10^{5}$
, and at separation is
![]() $2050$
based on the boundary layer thickness, corresponding to turbulent flow and a turbulent boundary layer separation.
$2050$
based on the boundary layer thickness, corresponding to turbulent flow and a turbulent boundary layer separation.
Appropriate forcing for interacting with the wake behind the axisymmetric bluff body was provided by a zero-net-mass-flux actuator. A high-fidelity loudspeaker (model Beyma 6P200ND) mounted inside the model was used to generate a pulsed jet of variable frequency and amplitude. The jet issues in the free-stream direction from a
![]() $2.0$
mm annular slit, located
$2.0$
mm annular slit, located
![]() $1.0$
mm below the trailing edge, as shown in figure 1(b). The jet velocity is uniform in the azimuthal direction, hence forcing is axisymmetric with azimuthal wavenumber
$1.0$
mm below the trailing edge, as shown in figure 1(b). The jet velocity is uniform in the azimuthal direction, hence forcing is axisymmetric with azimuthal wavenumber
![]() $m=0$
. A first-principles linear model relating the actuator driving signal (voltage) to its forcing output (centreline jet velocity) has been derived in appendix A.
$m=0$
. A first-principles linear model relating the actuator driving signal (voltage) to its forcing output (centreline jet velocity) has been derived in appendix A.
The circular rear face of the model was instrumented with 8 Endevco 8507C-1 piezoresistive pressure transducers equispaced in the azimuthal direction at
![]() $r/D=0.3$
. The sampling frequency was 20 KHz. Pressure measurements are expressed as a pressure coefficient, non-dimensionalised by the free-stream dynamic head
$r/D=0.3$
. The sampling frequency was 20 KHz. Pressure measurements are expressed as a pressure coefficient, non-dimensionalised by the free-stream dynamic head
![]() $0.5\unicode[STIX]{x1D70C}U_{\infty }^{2}$
. An important feature of the dynamic pressure transducers on the rear face of the model is that they allow the pressure distribution to be decomposed into azimuthal Fourier modes:
$0.5\unicode[STIX]{x1D70C}U_{\infty }^{2}$
. An important feature of the dynamic pressure transducers on the rear face of the model is that they allow the pressure distribution to be decomposed into azimuthal Fourier modes:
Depending on the amplitude values
![]() $p_{+m}$
and
$p_{+m}$
and
![]() $p_{-m}$
of the counter-rotating azimuthal modes, the decomposed wave can be a travelling wave, a standing wave or a combination of the last two.
$p_{-m}$
of the counter-rotating azimuthal modes, the decomposed wave can be a travelling wave, a standing wave or a combination of the last two.
4 Dynamic flow response to forcing
4.1 Unforced flow
The frequency premultiplied spectra of the unforced base-pressure fluctuations obtained from the eight pressure transducers at
![]() $r=0.3D$
, decomposed into azimuthal modes, are shown in figure 2. The Strouhal number is based on the body diameter and the free-stream velocity,
$r=0.3D$
, decomposed into azimuthal modes, are shown in figure 2. The Strouhal number is based on the body diameter and the free-stream velocity,
![]() $St=fD/U_{\infty }$
. A detailed analysis of the energetic regions of the spectra in the turbulent regime has been given in Rigas et al. (Reference Rigas, Oxlade, Morgans and Morrison2014).
$St=fD/U_{\infty }$
. A detailed analysis of the energetic regions of the spectra in the turbulent regime has been given in Rigas et al. (Reference Rigas, Oxlade, Morgans and Morrison2014).

Figure 2. Premultiplied spectra of the unforced base-pressure fluctuations obtained from the eight pressure transducers located at
![]() $r=0.3D$
, decomposed in azimuthal modes.
$r=0.3D$
, decomposed in azimuthal modes.
At very low frequencies (VLF),
![]() $St\approx 0.002$
and
$St\approx 0.002$
and
![]() $m=\pm 1$
, the energy content of the spectra is linked to random reorientations of the turbulent wake in the azimuthal direction. Similarly, random oscillations with broadband energy content occur around a frequency
$m=\pm 1$
, the energy content of the spectra is linked to random reorientations of the turbulent wake in the azimuthal direction. Similarly, random oscillations with broadband energy content occur around a frequency
![]() $St\approx 0.6$
and mainly with
$St\approx 0.6$
and mainly with
![]() $m=0$
, known in the literature as the ‘bubble-pumping mode’. These oscillations appear in the radial direction by examining the motion of the centre of pressure. A stochastic model describing this dynamic behaviour, which is linked to the random motion of the persisting steady symmetry break mode, has been proposed in Rigas et al. (Reference Rigas, Morgans, Brackston and Morrison2015).
$m=0$
, known in the literature as the ‘bubble-pumping mode’. These oscillations appear in the radial direction by examining the motion of the centre of pressure. A stochastic model describing this dynamic behaviour, which is linked to the random motion of the persisting steady symmetry break mode, has been proposed in Rigas et al. (Reference Rigas, Morgans, Brackston and Morrison2015).
Quasi-periodic oscillations with azimuthal wavenumber
![]() $m=\pm 1$
are identified at
$m=\pm 1$
are identified at
![]() $St\sim 0.2$
, corresponding to the vortex shedding (VS) mode. Recently performed direct numerical simulations and three-dimensional global stability analyses identify this mode as the primary unsteady mode undergoing a supercritical Hopf bifurcation in the laminar regime (Rigas, Esclapez & Magri Reference Rigas, Esclapez and Magri2016). Finally, in figure 2 quasi-periodic oscillations are identified at a frequency close to the subharmonic of the VS mode at
$St\sim 0.2$
, corresponding to the vortex shedding (VS) mode. Recently performed direct numerical simulations and three-dimensional global stability analyses identify this mode as the primary unsteady mode undergoing a supercritical Hopf bifurcation in the laminar regime (Rigas, Esclapez & Magri Reference Rigas, Esclapez and Magri2016). Finally, in figure 2 quasi-periodic oscillations are identified at a frequency close to the subharmonic of the VS mode at
![]() $St\approx 0.1$
for
$St\approx 0.1$
for
![]() $|m|=1,2$
. Time-resolved particle image velocimetry (not shown here) revealed that this mode is strong only close to the base of the body, in accordance also with the pressure measurements. Additionally, the VS mode is dominating the dynamic wake behaviour and reaches maximum amplitude close to the end of the recirculation bubble, which is approximately 1.5D downstream the base of the body.
$|m|=1,2$
. Time-resolved particle image velocimetry (not shown here) revealed that this mode is strong only close to the base of the body, in accordance also with the pressure measurements. Additionally, the VS mode is dominating the dynamic wake behaviour and reaches maximum amplitude close to the end of the recirculation bubble, which is approximately 1.5D downstream the base of the body.
4.2 Wake response
We experimentally examine the effect of flow forcing using axisymmetric (
![]() $m=0$
) slot jet actuation on the predominant modes present in the unforced flow. The turbulent wake was excited driving the actuator with a harmonic voltage signal, as in the work of Oxlade et al. (Reference Oxlade, Morrison, Qubain and Rigas2015). A wide range of forcing amplitudes and frequencies was explored during the experiments and the results are presented here.
$m=0$
) slot jet actuation on the predominant modes present in the unforced flow. The turbulent wake was excited driving the actuator with a harmonic voltage signal, as in the work of Oxlade et al. (Reference Oxlade, Morrison, Qubain and Rigas2015). A wide range of forcing amplitudes and frequencies was explored during the experiments and the results are presented here.

Figure 3. The response of the amplitude (a) and frequency (b) of the
![]() $m=\pm 1$
global vortex shedding mode to axisymmetric forcing with
$m=\pm 1$
global vortex shedding mode to axisymmetric forcing with
![]() $m=0$
at different forcing frequencies. The results for two forcing amplitudes,
$m=0$
at different forcing frequencies. The results for two forcing amplitudes,
![]() $U_{jet}/U_{\infty }$
, are shown corresponding to
$U_{jet}/U_{\infty }$
, are shown corresponding to
![]() $+1$
(○) and
$+1$
(○) and
![]() $-1$
(
$-1$
(
![]() $+$
) modes.
$+$
) modes.
The forced spectra of the azimuthally decomposed base pressure were inspected for changes and compared to the unforced ones. During all forcing conditions, a dominant response was identified at the forcing wavenumber,
![]() $m_{f}=0$
, and frequency
$m_{f}=0$
, and frequency
![]() $St_{f}=\unicode[STIX]{x1D714}_{f}/2\unicode[STIX]{x03C0}$
, as expected in a linear framework. In the spectra of base pressure, a sharp peak appears in the
$St_{f}=\unicode[STIX]{x1D714}_{f}/2\unicode[STIX]{x03C0}$
, as expected in a linear framework. In the spectra of base pressure, a sharp peak appears in the
![]() $m=0$
mode. However, a pronounced change was also observed in the spectra of the
$m=0$
mode. However, a pronounced change was also observed in the spectra of the
![]() $|m|=1$
mode, near
$|m|=1$
mode, near
![]() $St=0.2$
, which coincides with the frequency of the global shedding mode. This behaviour is indicative of the inherent nonlinearity of the fluid system. The steady-state amplitude and frequency response of the
$St=0.2$
, which coincides with the frequency of the global shedding mode. This behaviour is indicative of the inherent nonlinearity of the fluid system. The steady-state amplitude and frequency response of the
![]() $m=\pm 1$
global shedding mode to axisymmetric forcing over different forcing frequencies and amplitudes are shown in figure 3. The amplitude of the vortex shedding mode was estimated by integrating the
$m=\pm 1$
global shedding mode to axisymmetric forcing over different forcing frequencies and amplitudes are shown in figure 3. The amplitude of the vortex shedding mode was estimated by integrating the
![]() $m=\pm 1$
pressure spectra around the frequency of the shedding mode (
$m=\pm 1$
pressure spectra around the frequency of the shedding mode (
![]() $St_{VS}$
,
$St_{VS}$
,
![]() $\unicode[STIX]{x0394}St=0.01$
):
$\unicode[STIX]{x0394}St=0.01$
):
Due to the fact that the frequency of the shedding mode varies depending on the forcing amplitude and frequency, its frequency was estimated as the frequency of the maximum amplitude close to
![]() $St=0.2$
.
$St=0.2$
.
The amplitude response is indistinguishable for the
![]() $m=+1$
and
$m=+1$
and
![]() $m=-1$
modes at the VS frequency, meaning
$m=-1$
modes at the VS frequency, meaning
![]() $A_{VS}\equiv A_{+}=A_{-}$
for the entire frequency and amplitude range of the forcing. Since the amplitudes of the two counter-rotating decomposed modes are the same, it is concluded that the shedding is a standing mode in the presence of axisymmetric forcing.
$A_{VS}\equiv A_{+}=A_{-}$
for the entire frequency and amplitude range of the forcing. Since the amplitudes of the two counter-rotating decomposed modes are the same, it is concluded that the shedding is a standing mode in the presence of axisymmetric forcing.
4.3 Vortex shedding: parametric subharmonic resonance
A strong resonance in the response occurs when the forcing is close to twice the global-mode frequency,
![]() $St_{f}\approx 2St_{VS}=0.4$
, as shown in figure 3. Near this forcing frequency, the frequency of the global mode ‘locks-in’ to one-half the forcing frequency. The lock-in region depends on the forcing amplitude; increasing amplitude results in a wider lock-in range.
$St_{f}\approx 2St_{VS}=0.4$
, as shown in figure 3. Near this forcing frequency, the frequency of the global mode ‘locks-in’ to one-half the forcing frequency. The lock-in region depends on the forcing amplitude; increasing amplitude results in a wider lock-in range.
Similar frequency lock-in behaviour has been observed experimentally before for three-dimensional bluff-body wakes. Kim & Durbin (Reference Kim and Durbin1988) examined the wake of a sphere under acoustic excitation for Reynolds number 3700. In their experiments, the shedding frequency also locked-in to one-half the forcing frequency, with no such effect when forcing near to the shedding frequency. Also, Bigger, Higuchi & Hall (Reference Bigger, Higuchi and Hall2009) examined the forced wake of a disk under helical and symmetric actuation, and found that the most effective frequency to reduce the length of the recirculation zone corresponds to the natural shedding frequency and twice that, for the two types of actuation, respectively. Recently, Barros et al. (Reference Barros, Borée, Noack and Spohn2016) found that symmetric pulsed-jet forcing can lead to subharmonic resonance of the antisymmetric vortex shedding mode observed in the square-back Ahmed body, when forcing is applied close to twice the shedding frequency.
Lock-in phenomena point to nonlinear oscillator behaviour forcing past a suspected global-mode frequency or its rational multiples (Huerre & Monkewitz Reference Huerre and Monkewitz1990). Hence, a nonlinear coupling between the forcing (
![]() $m=0$
) and the unsteady global (
$m=0$
) and the unsteady global (
![]() $m=\pm 1$
) modes exists. The results indicate that the dominant interaction is a parametric resonance mechanism between the fundamental forcing and the subharmonic modes which leads to a pronounced growth of the subharmonic. This parametric subharmonic instability (PSI), is a resonant wave–triad interaction characterised by transfer of energy from a parent wave to two daughter waves of half-frequency and higher wavenumber (Craik Reference Craik1988). The resonant conditions are
$m=\pm 1$
) modes exists. The results indicate that the dominant interaction is a parametric resonance mechanism between the fundamental forcing and the subharmonic modes which leads to a pronounced growth of the subharmonic. This parametric subharmonic instability (PSI), is a resonant wave–triad interaction characterised by transfer of energy from a parent wave to two daughter waves of half-frequency and higher wavenumber (Craik Reference Craik1988). The resonant conditions are
The resonant triadic interaction between axisymmetric forcing and antisymmetric vortex shedding is depicted in the spectra of the azimuthally decomposed pressure in figure 4, where the results of a specific forcing frequency and amplitude are presented. Forcing at
![]() $St_{f}=0.40$
, the spectra of the pressure are dominated by the linear response of the axisymmetric mode at the forcing frequency (
$St_{f}=0.40$
, the spectra of the pressure are dominated by the linear response of the axisymmetric mode at the forcing frequency (
![]() $St=0.4$
) and the nonlinear subharmonic response of the global mode at half the forcing frequency (
$St=0.4$
) and the nonlinear subharmonic response of the global mode at half the forcing frequency (
![]() $St=0.2$
). Interestingly, all the other spectral peaks observed in the unforced case have been suppressed except the broadband axisymmetric mode at
$St=0.2$
). Interestingly, all the other spectral peaks observed in the unforced case have been suppressed except the broadband axisymmetric mode at
![]() $St\approx 0.06$
which is still present in the base-pressure measurements. The suppressed modes of the wake are the random VLF mode near
$St\approx 0.06$
which is still present in the base-pressure measurements. The suppressed modes of the wake are the random VLF mode near
![]() $St\approx 0.002$
and the quasi-periodic motion close to the subharmonic of the VS mode at
$St\approx 0.002$
and the quasi-periodic motion close to the subharmonic of the VS mode at
![]() $St\approx 0.1$
. The suppression of the VLF mode fixes the angle of the reflectional symmetry plane on the base of the body and no random meandering is observed when harmonic forcing is applied, as opposed to the unforced case. In conclusion, for the PSI case, the VS mode is dominating the forced response over the entire near wake.
$St\approx 0.1$
. The suppression of the VLF mode fixes the angle of the reflectional symmetry plane on the base of the body and no random meandering is observed when harmonic forcing is applied, as opposed to the unforced case. In conclusion, for the PSI case, the VS mode is dominating the forced response over the entire near wake.

Figure 4. The effect of axisymmetric forcing at
![]() $St_{f}=2St_{VS}=0.4$
on the spectra of (a)
$St_{f}=2St_{VS}=0.4$
on the spectra of (a)
![]() $m=0$
and (b)
$m=0$
and (b)
![]() $|m|=1$
mode. The forcing results in parametric subharmonic resonance (PSI) of the
$|m|=1$
mode. The forcing results in parametric subharmonic resonance (PSI) of the
![]() $|m|=1$
shedding mode at
$|m|=1$
shedding mode at
![]() $St_{VS}=0.2$
.
$St_{VS}=0.2$
.
The amplitude and frequency values of the VS mode, as a function of the forcing amplitude
![]() $U_{jet}$
, are shown in figure 5. The response of the shedding amplitude follows a nonlinear trend as the forcing amplitude increases. Also, at low forcing amplitudes the shedding mode appears to be insensitive to forcing, meaning that a minimum forcing amplitude is required to excite parametrically the VS. This threshold, when forcing with a small detuning at
$U_{jet}$
, are shown in figure 5. The response of the shedding amplitude follows a nonlinear trend as the forcing amplitude increases. Also, at low forcing amplitudes the shedding mode appears to be insensitive to forcing, meaning that a minimum forcing amplitude is required to excite parametrically the VS. This threshold, when forcing with a small detuning at
![]() $St_{f}\approx 0.40$
, is
$St_{f}\approx 0.40$
, is
![]() $U_{jet}\approx 0.05U_{\infty }$
. The same forcing amplitude threshold exists in order to lock in the frequency of the VS mode.
$U_{jet}\approx 0.05U_{\infty }$
. The same forcing amplitude threshold exists in order to lock in the frequency of the VS mode.

Figure 5. Steady-state response of the global vortex shedding mode with
![]() $m=\pm 1$
to periodic zero-net-mass-flux forcing with azimuthal wavenumber
$m=\pm 1$
to periodic zero-net-mass-flux forcing with azimuthal wavenumber
![]() $m_{f}=0$
and frequencies
$m_{f}=0$
and frequencies
![]() $St_{f}$
close to twice the global mode frequency; (a) amplitude and (b) frequency.
$St_{f}$
close to twice the global mode frequency; (a) amplitude and (b) frequency.
To summarise, the unsteady global mode of the flow is known to be the shedding mode, with azimuthal wavenumbers
![]() $m=\pm 1$
and frequency
$m=\pm 1$
and frequency
![]() $St\approx 0.2$
. Axisymmetric harmonic forcing couples nonlinearly with this global mode, with this coupling being the main factor that determines the flow field response. Spectral peaks close to the subharmonic of the global mode, and the very low frequency random rotation of the wake which were present in the unforced spectrum, are suppressed on applying forcing. We therefore conclude that any mathematical attempt to predict the effect of forcing on the flow field must retain at least the global
$St\approx 0.2$
. Axisymmetric harmonic forcing couples nonlinearly with this global mode, with this coupling being the main factor that determines the flow field response. Spectral peaks close to the subharmonic of the global mode, and the very low frequency random rotation of the wake which were present in the unforced spectrum, are suppressed on applying forcing. We therefore conclude that any mathematical attempt to predict the effect of forcing on the flow field must retain at least the global
![]() $m=\pm 1$
modes, along with their coupling with the axisymmetric
$m=\pm 1$
modes, along with their coupling with the axisymmetric
![]() $m=0$
forcing.
$m=0$
forcing.
5 Dynamic modelling
We consider the flow behind the axisymmetric bluff body and we derive amplitude equations governing the forced amplitude evolution of the vortex shedding global mode for the turbulent axisymmetric wake in the presence of external forcing. The governing equations are the incompressible Navier–Stokes equations (2.1).
5.1 Flow decomposition
For a large departure from criticality, where
![]() $Re\gg 1$
, the separating boundary layer and the near wake are turbulent resulting in the generation of small-scale incoherent motion in localised regions in space and time. Since the near-wake turbulent flow contains structures of widely separated time and length scales, which may interact despite their large scale separation, we consider a model employing scale subdivision with the large scales accounting for the coherent structures and the small scales involving the incoherent background. Then, the instantaneous flow quantities
$Re\gg 1$
, the separating boundary layer and the near wake are turbulent resulting in the generation of small-scale incoherent motion in localised regions in space and time. Since the near-wake turbulent flow contains structures of widely separated time and length scales, which may interact despite their large scale separation, we consider a model employing scale subdivision with the large scales accounting for the coherent structures and the small scales involving the incoherent background. Then, the instantaneous flow quantities
![]() $\boldsymbol{q}=(\boldsymbol{u},p)^{\text{T}}$
can be decomposed as:
$\boldsymbol{q}=(\boldsymbol{u},p)^{\text{T}}$
can be decomposed as:
where
![]() $\boldsymbol{q}_{0}$
is a base flow at
$\boldsymbol{q}_{0}$
is a base flow at
![]() $Re_{c}$
,
$Re_{c}$
,
![]() $\tilde{\boldsymbol{q}}$
the contribution of the global modes (coherent part) and
$\tilde{\boldsymbol{q}}$
the contribution of the global modes (coherent part) and
![]() $\boldsymbol{q}^{\prime }$
the turbulence (incoherent part). The time-independent base flow
$\boldsymbol{q}^{\prime }$
the turbulence (incoherent part). The time-independent base flow
![]() $\boldsymbol{q}_{0}$
is a steady solution of the Navier–Stokes equations at
$\boldsymbol{q}_{0}$
is a steady solution of the Navier–Stokes equations at
![]() $Re_{c}$
:
$Re_{c}$
:
The base flow modifications due to departure from
![]() $Re_{c}$
and the nonlinear interactions of the waves are given from the mean component of the coherent wave whereas the turbulence is considered of random nature with zero mean. Similar to Reynolds & Hussain (Reference Reynolds and Hussain1972), we define time-averaged and the phase-averaged quantities as
$Re_{c}$
and the nonlinear interactions of the waves are given from the mean component of the coherent wave whereas the turbulence is considered of random nature with zero mean. Similar to Reynolds & Hussain (Reference Reynolds and Hussain1972), we define time-averaged and the phase-averaged quantities as
with
![]() $\unicode[STIX]{x1D70F}$
being the period of the quasi-periodic vortex shedding mode. Applying (5.3), the time- and phase-averaged flow quantities are:
$\unicode[STIX]{x1D70F}$
being the period of the quasi-periodic vortex shedding mode. Applying (5.3), the time- and phase-averaged flow quantities are:
Both averaging operations remove the incoherent contribution of turbulence. Then the mean flow is given as the superposition of a base flow and the mean flow modification of the coherent waves.
5.2 Governing equations for the turbulent flow
Substituting the decomposition (5.1) into the Navier–Stokes equations (2.1) and phase averaging, one finds the following equations:
Or equivalently:
The right-hand side term of equation (5.7) involves the contribution of the Reynolds stress of the phase-averaged random turbulence. The phase-averaged form of the Navier–Stokes equations cannot by themselves determine the phase-averaged quantities; one must also provide a relation between the random fluctuating and averaged quantities. For laminar flows and close to the threshold of the instability the amplitude evolution of the coherent waves (linearly unstable modes) can be found using a weakly nonlinear expansion (Meliga et al.
Reference Meliga, Chomaz and Sipp2009); in this case
![]() $\boldsymbol{u}^{\prime }\equiv 0$
since the flow is laminar. The weakly nonlinear analysis can be extended also in the turbulent regime by introducing an eddy viscosity closure for the incoherent Reynolds stresses:
$\boldsymbol{u}^{\prime }\equiv 0$
since the flow is laminar. The weakly nonlinear analysis can be extended also in the turbulent regime by introducing an eddy viscosity closure for the incoherent Reynolds stresses:
Despite its limitations, this approach has been successfully used in various studies for the prediction of global modes through stability analysis of turbulent time-averaged flows (Meliga, Pujals & Serre Reference Meliga, Pujals and Serre2012; Tammisola & Juniper Reference Tammisola and Juniper2016) and base flows obtained by Reynolds-averaged Navier–Stokes equations (Mettot, Sipp & Bézard Reference Mettot, Sipp and Bézard2014) in a linearised framework. Under this assumption, equation (5.7) becomes:
Here,
![]() $Re_{T}=(U_{\infty }D)/(\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{t})$
, where
$Re_{T}=(U_{\infty }D)/(\unicode[STIX]{x1D708}+\unicode[STIX]{x1D708}_{t})$
, where
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
![]() $\unicode[STIX]{x1D708}_{t}$
the turbulent eddy viscosity, where it is expected that
$\unicode[STIX]{x1D708}_{t}$
the turbulent eddy viscosity, where it is expected that
![]() $\unicode[STIX]{x1D708}_{t}\gg \unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}_{t}\gg \unicode[STIX]{x1D708}$
.
5.3 Weakly nonlinear analysis
The turbulent wake exhibits global modes with azimuthal wavenumbers
![]() $+1$
and
$+1$
and
![]() $-1$
. It therefore has at least a pair of complex eigenvalues with azimuthal wavenumbers
$-1$
. It therefore has at least a pair of complex eigenvalues with azimuthal wavenumbers
![]() $+1$
and
$+1$
and
![]() $-1$
, which manifest as organised waves in the turbulent flow. In the present analysis, we focus on the derivation of the response of the global modes to external forcing. The weakly nonlinear analysis can be applied to derive the amplitude equations of the unstable modes. For this, we follow the analysis proposed by Sipp (Reference Sipp2012) for the laminar open-cavity flow but now for the three-dimensional axisymmetric turbulent wake.
$-1$
, which manifest as organised waves in the turbulent flow. In the present analysis, we focus on the derivation of the response of the global modes to external forcing. The weakly nonlinear analysis can be applied to derive the amplitude equations of the unstable modes. For this, we follow the analysis proposed by Sipp (Reference Sipp2012) for the laminar open-cavity flow but now for the three-dimensional axisymmetric turbulent wake.
The departure from the critical Reynolds number,
![]() $Re_{c}$
, where the stability is lost, can be expressed as:
$Re_{c}$
, where the stability is lost, can be expressed as:
Assuming that the turbulent Reynolds number is close and above the critical one, we can write
We introduce a fast time scale
![]() $t$
and a slow time scale
$t$
and a slow time scale
![]() $t_{1}=\unicode[STIX]{x1D700}t$
. Then, the turbulent phase-averaged field
$t_{1}=\unicode[STIX]{x1D700}t$
. Then, the turbulent phase-averaged field
![]() $\langle \boldsymbol{q}\rangle$
can be expanded around a base flow at criticality as
$\langle \boldsymbol{q}\rangle$
can be expanded around a base flow at criticality as
Introducing (5.11) and (5.12) into (5.9), and equating coefficients of the
![]() $n$
th power of
$n$
th power of
![]() $\sqrt{\unicode[STIX]{x1D700}}$
to zero, a series of equations is obtained at various orders (see appendix B).
$\sqrt{\unicode[STIX]{x1D700}}$
to zero, a series of equations is obtained at various orders (see appendix B).
For non-resonant forcing at order
![]() $\sqrt{\unicode[STIX]{x1D700}}$
, the solution of the equations is sought in the form
$\sqrt{\unicode[STIX]{x1D700}}$
, the solution of the equations is sought in the form
and consists of the superposition of the global mode and the forcing response, with amplitudes
![]() $A_{VS}=A_{+}=A_{-}$
and
$A_{VS}=A_{+}=A_{-}$
and
![]() $E$
, and spatial structures
$E$
, and spatial structures
![]() $q_{1}^{A}=q_{1}^{A}(r,z)$
and
$q_{1}^{A}=q_{1}^{A}(r,z)$
and
![]() $q_{1}^{E}=q_{1}^{E}(r,z)$
, respectively. At order
$q_{1}^{E}=q_{1}^{E}(r,z)$
, respectively. At order
![]() $\sqrt{\unicode[STIX]{x1D700}}^{3}$
, compatibility conditions have to be imposed for the solvability of the equations (Sipp & Lebedev Reference Sipp and Lebedev2007; Meliga et al.
Reference Meliga, Chomaz and Sipp2009; Sipp Reference Sipp2012; Orchini, Rigas & Juniper Reference Orchini, Rigas and Juniper2016). These conditions yield the following equation governing the complex amplitude
$\sqrt{\unicode[STIX]{x1D700}}^{3}$
, compatibility conditions have to be imposed for the solvability of the equations (Sipp & Lebedev Reference Sipp and Lebedev2007; Meliga et al.
Reference Meliga, Chomaz and Sipp2009; Sipp Reference Sipp2012; Orchini, Rigas & Juniper Reference Orchini, Rigas and Juniper2016). These conditions yield the following equation governing the complex amplitude
![]() $A_{VS}$
of the global mode:
$A_{VS}$
of the global mode:
The complex parameters
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D706}$
are the linear growth rate and the saturation coefficient. The function
$\unicode[STIX]{x1D706}$
are the linear growth rate and the saturation coefficient. The function
![]() $g$
contains all the secular terms that stem from the interaction of the global mode with the forcing at third order. In the absence of external forcing, the function
$g$
contains all the secular terms that stem from the interaction of the global mode with the forcing at third order. In the absence of external forcing, the function
![]() $g$
is zero and the well-known Stuart–Landau equation is obtained.
$g$
is zero and the well-known Stuart–Landau equation is obtained.
When
![]() $\unicode[STIX]{x1D714}_{f}$
is close to twice the global shedding mode frequency, we have seen in figure 4 that the flow responds significantly in azimuthal wavenumber
$\unicode[STIX]{x1D714}_{f}$
is close to twice the global shedding mode frequency, we have seen in figure 4 that the flow responds significantly in azimuthal wavenumber
![]() $|m|=1$
at half the forcing frequency. Thus forcing at frequencies close to twice the shedding frequency (i.e.
$|m|=1$
at half the forcing frequency. Thus forcing at frequencies close to twice the shedding frequency (i.e.
![]() $St\approx 0.4$
) will be termed ‘resonant forcing’. For resonant forcing, we have the superimposition of two counter-rotating modes of same amplitude
$St\approx 0.4$
) will be termed ‘resonant forcing’. For resonant forcing, we have the superimposition of two counter-rotating modes of same amplitude
![]() $A_{VS}$
, and (5.14) has the following form:
$A_{VS}$
, and (5.14) has the following form:
The last term in (5.15) results from the nonlinear coupling between the complex conjugate of the global mode
![]() $A_{VS}^{\ast }$
and the axisymmetric forcing
$A_{VS}^{\ast }$
and the axisymmetric forcing
![]() $E$
, when forcing is applied resonantly near twice the global-mode frequency.
$E$
, when forcing is applied resonantly near twice the global-mode frequency.
5.4 Identification of model parameters
In order to identify the unknown complex parameters,
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D707}$
, of (5.15), further forced experiments are performed. The system is subject to harmonic excitation, modelled through the forcing term
$\unicode[STIX]{x1D707}$
, of (5.15), further forced experiments are performed. The system is subject to harmonic excitation, modelled through the forcing term
![]() $E$
, and the transient response of the unsteady global shedding mode is measured. The non-dimensional centreline velocity of the jet output is used to quantify the forcing amplitude
$E$
, and the transient response of the unsteady global shedding mode is measured. The non-dimensional centreline velocity of the jet output is used to quantify the forcing amplitude
![]() $E$
, that is
$E$
, that is
![]() $E=U_{jet}/U_{\infty }$
. Substituting
$E=U_{jet}/U_{\infty }$
. Substituting
![]() $A_{VS}=|A_{VS}|\text{e}^{\text{i}\unicode[STIX]{x1D714}t}$
and
$A_{VS}=|A_{VS}|\text{e}^{\text{i}\unicode[STIX]{x1D714}t}$
and
![]() $E=|E|\text{e}^{\text{i}\unicode[STIX]{x1D714}_{f}t}$
, for
$E=|E|\text{e}^{\text{i}\unicode[STIX]{x1D714}_{f}t}$
, for
![]() $\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x1D714}_{c}$
, yields the following equations for the modulus and phase of the unsteady global mode:
$\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x1D714}_{c}$
, yields the following equations for the modulus and phase of the unsteady global mode:
-
(i) The measured pressure signals on the base of the body are decomposed in the azimuthal direction to obtain the first azimuthal Fourier components corresponding to
 $m=\pm 1$
.
$m=\pm 1$
. -
(ii) The signal is then bandpass filtered in the spectral domain with a window centred on the frequency of the vortex shedding mode to obtain
 $A_{VS}(t)$
.
$A_{VS}(t)$
. -
(iii) The instantaneous complex amplitude
 $(A_{r}+\text{i}A_{i})(t)$
of the vortex shedding global mode is built from the Hilbert transform.
$(A_{r}+\text{i}A_{i})(t)$
of the vortex shedding global mode is built from the Hilbert transform. -
(iv) Then, the instantaneous amplitude and phase are given by
 $|A_{VS}|=\sqrt{A_{r}^{2}+A_{i}^{2}}$
and
$|A_{VS}|=\sqrt{A_{r}^{2}+A_{i}^{2}}$
and
 $\unicode[STIX]{x1D719}=\tan ^{-1}(A_{r}/A_{i})$
.
$\unicode[STIX]{x1D719}=\tan ^{-1}(A_{r}/A_{i})$
. -
(v) The growth rate
 $\text{d}|A_{VS}|/\text{d}t$
and frequency
$\text{d}|A_{VS}|/\text{d}t$
and frequency
 $\unicode[STIX]{x1D714}$
are calculated by differentiating in time the instantaneous amplitude and phase. Time derivatives are evaluated by finite differences.
$\unicode[STIX]{x1D714}$
are calculated by differentiating in time the instantaneous amplitude and phase. Time derivatives are evaluated by finite differences.

Figure 6. Fitting of unknown coefficients of (5.16b
) for
![]() $\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x1D714}_{c}$
using experimental transient data from the shedding response to three forcing amplitudes
$\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x1D714}_{c}$
using experimental transient data from the shedding response to three forcing amplitudes
![]() $U_{jet}/U_{\infty }$
, 0.33 (blue), 0.41 (red), 0.49 (yellow). (a,b) Fitted planes and experimental transient data (symbols); (c,d) and (e,f) two different views of the fitted planes. (a,c,e) Amplitude (real part); (b,d,f) frequency (imaginary part).
$U_{jet}/U_{\infty }$
, 0.33 (blue), 0.41 (red), 0.49 (yellow). (a,b) Fitted planes and experimental transient data (symbols); (c,d) and (e,f) two different views of the fitted planes. (a,c,e) Amplitude (real part); (b,d,f) frequency (imaginary part).
A similar procedure to the one described above for the identification of the Landau coefficients has been applied close to the threshold of bifurcation for the velocity signal in the wake of a cylinder (Schumm, Berger & Monkewitz Reference Schumm, Berger and Monkewitz1994). When transients are contaminated by noise, the instantaneous growth rates and frequencies determined in this fashion are only reliable where the signal-to-noise ratio is significantly above unity. The irregularity of the forced transient data was pronounced in the present measurements due to the high turbulent activity in the near wake, despite the bandpass filtering of the signal around the shedding frequency. This problem was tackled by phase averaging over a number of experiments using as a reference signal the forcing signal. In effect, the phase-averaging procedure rejects the background turbulence and extracts only the organised motions from the total signal (Reynolds & Hussain Reference Reynolds and Hussain1972). The averaging procedure produced smooth transient responses, which also facilitated the calculation of relevant derivatives for calculating instantaneous growth rates and frequencies. Averaging was performed here over 50 transient data sets to obtain an average of the amplitude
![]() $|A(t)|$
and the instantaneous frequency
$|A(t)|$
and the instantaneous frequency
![]() $\unicode[STIX]{x1D714}(t)$
.
$\unicode[STIX]{x1D714}(t)$
.
After computing the above phase-averaged transient quantities and their derivatives, in order to obtain growth rates and frequencies, the identification of the unknown coefficients is performed by least squares fitting. Inspection of (5.16a
) and (5.16b
) reveals that the left-hand side of the equations lie on two planes, i.e. of the form
![]() $y=c_{0}+c_{1}x_{1}+c_{2}x_{2}$
, as shown in figure 6. The growth rates, frequencies and amplitudes used for the fitting describe the transient behaviour of the vortex shedding from the unforced limit cycle to the saturated amplitude and frequency, for various forcing amplitudes. The fitted parameters, obtained by least squares fitting, are given in table 1. Finally, it should be noted that an alternative way to perform the fitting would be by using only steady-state data. This approach was not followed here in order to evaluate the predictability of the model during the transient regimes. In both cases, longer time series reduce the error of the fitting.
$y=c_{0}+c_{1}x_{1}+c_{2}x_{2}$
, as shown in figure 6. The growth rates, frequencies and amplitudes used for the fitting describe the transient behaviour of the vortex shedding from the unforced limit cycle to the saturated amplitude and frequency, for various forcing amplitudes. The fitted parameters, obtained by least squares fitting, are given in table 1. Finally, it should be noted that an alternative way to perform the fitting would be by using only steady-state data. This approach was not followed here in order to evaluate the predictability of the model during the transient regimes. In both cases, longer time series reduce the error of the fitting.
Table 1. Values of non-dimensional model parameters obtained from data fitting.
5.5 Model validation
In order to validate the coupled Stuart–Landau equations that resulted from the weakly nonlinear analysis, including the complex coefficient values obtained from experiments, the version of the equation valid for resonant forcing, equation (5.15), is now used to predict some features of the forced response. These predictions will be compared to experimental measurements.
We begin by revisiting figure 3, in which the response of the global
![]() $m=\pm 1$
shedding mode to axisymmetric forcing was presented for a range of frequencies and two forcing amplitudes, exhibiting amplitude resonance and frequency lock-in when forcing was applied near twice the global-mode frequency. The model predictions, are shown in figure 7, overlaid with the experimental results. The steady-state amplitude and frequency response obtained from the model are shown as a function of forcing frequency for the two experimental forcing amplitudes. It is clear that the model captures the frequency lock-in effect and the parametric subharmonic resonance, as observed in the wind tunnel measurements.
$m=\pm 1$
shedding mode to axisymmetric forcing was presented for a range of frequencies and two forcing amplitudes, exhibiting amplitude resonance and frequency lock-in when forcing was applied near twice the global-mode frequency. The model predictions, are shown in figure 7, overlaid with the experimental results. The steady-state amplitude and frequency response obtained from the model are shown as a function of forcing frequency for the two experimental forcing amplitudes. It is clear that the model captures the frequency lock-in effect and the parametric subharmonic resonance, as observed in the wind tunnel measurements.

Figure 7. The response of the amplitude and frequency of the
![]() $m=\pm 1$
vortex shedding mode to axisymmetric forcing with
$m=\pm 1$
vortex shedding mode to axisymmetric forcing with
![]() $m=0$
at different forcing frequencies. Model predictions (lines) and experimental data (symbols).
$m=0$
at different forcing frequencies. Model predictions (lines) and experimental data (symbols).
The effect of forcing amplitude on the shedding mode response is now considered for the PSI. The model predictions are compared with the experimental results in figure 8. The response in
![]() $|m|=1$
is nonlinear; when a certain forcing amplitude is reached, frequency lock-in occurs and the amplitude rises sharply. This effect is also well predicted by the model. Thus it is clear that the low-dimensional, weakly nonlinear model is capturing the main features of the response of the global shedding mode. However, it is observed that the quantitative accuracy of the model deteriorates towards lower forcing amplitudes, as seen in figures 7 and 8.
$|m|=1$
is nonlinear; when a certain forcing amplitude is reached, frequency lock-in occurs and the amplitude rises sharply. This effect is also well predicted by the model. Thus it is clear that the low-dimensional, weakly nonlinear model is capturing the main features of the response of the global shedding mode. However, it is observed that the quantitative accuracy of the model deteriorates towards lower forcing amplitudes, as seen in figures 7 and 8.

Figure 8. Steady-state response of the global vortex shedding mode to zero-net-mass-flux harmonic forcing with azimuthal wavenumber
![]() $m=0$
and two frequencies close to twice the global-mode frequency; amplitude (a) and frequency (b).
$m=0$
and two frequencies close to twice the global-mode frequency; amplitude (a) and frequency (b).
6 Conclusions
We have derived Landau-like models to capture the weakly nonlinear interaction between the global modes and axisymmetric forcing at high Reynolds numbers. These ideas have previously been applied only to laminar wakes. The models were validated performing experiments on the three-dimensional wake of an axisymmetric bluff body, incorporating an axisymmetric zero-net-mass-flux actuator on the base of the body. With the present experiments we have demonstrated that the concept of weakly nonlinear global modes can be extended to a fully turbulent flow, far away from the critical bifurcation Reynolds number.
Key advantage of the models is that the dynamics of the forcing is explicitly included in the Landau models and the unknown coefficients are identified from forced experiments. We derived and validated the models for specific forcing conditions
![]() $(\unicode[STIX]{x1D714}_{f},m_{f})=(2\unicode[STIX]{x1D714}_{c},0)$
. The specific choice was made due to the high sensitivity of the global mode close to this forcing frequency, which could be beneficial in feedback control designs (Pastoor et al.
Reference Pastoor, Henning, Noack, King and Tadmor2008; Brackston et al.
Reference Brackston, Garcia de la Cruz, Wynn, Rigas and Morrison2016). Also, the combination of the actuator transfer function with the wake dynamics given by the Landau models, gives the full transfer function between physical input to the actuator and measured output of the fluid system. These low-order models can be used as a basis for feedback control designs for the suppression of the large-scale shedding observed in the wake of three-dimensional bluff bodies.
$(\unicode[STIX]{x1D714}_{f},m_{f})=(2\unicode[STIX]{x1D714}_{c},0)$
. The specific choice was made due to the high sensitivity of the global mode close to this forcing frequency, which could be beneficial in feedback control designs (Pastoor et al.
Reference Pastoor, Henning, Noack, King and Tadmor2008; Brackston et al.
Reference Brackston, Garcia de la Cruz, Wynn, Rigas and Morrison2016). Also, the combination of the actuator transfer function with the wake dynamics given by the Landau models, gives the full transfer function between physical input to the actuator and measured output of the fluid system. These low-order models can be used as a basis for feedback control designs for the suppression of the large-scale shedding observed in the wake of three-dimensional bluff bodies.
Acknowledgements
This research was sponsored by the Engineering and Physical Sciences Research Council (EPSRC), under grant EP/I005684. We are also indebted to the Imperial College EPSRC Impact Acceleration Account for financial support.
Appendix A. Actuator modelling
A simple linear model is used to describe the zero-net-mass-flux actuator dynamics and relate the input (driving voltage) with the output (jet velocity). The basic components of the actuator are an oscillatory diaphragm (here loudspeaker), a cavity and an orifice, as shown schematically in figure 9. The relations among actuator deflection
![]() $x_{d}$
, cavity pressure
$x_{d}$
, cavity pressure
![]() $p_{cav}$
and jet velocity
$p_{cav}$
and jet velocity
![]() $u_{jet}$
are described by the following linear differential equations (Persoons & O’Donovan Reference Persoons and O’Donovan2007; Persoons Reference Persoons2012):
$u_{jet}$
are described by the following linear differential equations (Persoons & O’Donovan Reference Persoons and O’Donovan2007; Persoons Reference Persoons2012):

Figure 9. Schematic of the zero-net-mass-flux actuator.
Conservation of mass in the cavity, combined with ideal gas law and assuming adiabatic compression/expansion:
Conservation of momentum in the orifice, assuming linear damping force:
The relations linking driving voltage
![]() $v_{in}$
and current
$v_{in}$
and current
![]() $i_{in}$
with
$i_{in}$
with
![]() $x_{d}$
and
$x_{d}$
and
![]() $p_{cav}$
are given by the governing equations of the electromagnetic system (voice coil diaphragm). These are
$p_{cav}$
are given by the governing equations of the electromagnetic system (voice coil diaphragm). These are
where
![]() $F_{d}=Bli_{in}$
is the electromagnetic force produced by the current in the coil.
$F_{d}=Bli_{in}$
is the electromagnetic force produced by the current in the coil.
We apply the Laplace transform on the differential equations (A 1)–(A 4) to obtain polynomials in
![]() $s=j\unicode[STIX]{x1D714}$
, the Laplace variable (time domain to the complex frequency domain). Solving for
$s=j\unicode[STIX]{x1D714}$
, the Laplace variable (time domain to the complex frequency domain). Solving for
![]() $U/V$
, we find the following transfer function between output jet velocity and driving voltage:
$U/V$
, we find the following transfer function between output jet velocity and driving voltage:
 $$\begin{eqnarray}\displaystyle \frac{U_{jet}(s)}{V_{in}(s)}=\frac{K_{1}\,s}{\underbrace{(s+\unicode[STIX]{x1D714}_{3})}_{\mathit{Coil}}\underbrace{(s^{2}+2\unicode[STIX]{x1D701}\unicode[STIX]{x1D714}_{2}s+{\unicode[STIX]{x1D714}_{2}}^{2})}_{\mathit{Helmholtz}}\underbrace{(s^{2}+2\unicode[STIX]{x1D701}\unicode[STIX]{x1D714}_{1}s+{\unicode[STIX]{x1D714}_{1}}^{2})}_{\mathit{Diaphragm}}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{U_{jet}(s)}{V_{in}(s)}=\frac{K_{1}\,s}{\underbrace{(s+\unicode[STIX]{x1D714}_{3})}_{\mathit{Coil}}\underbrace{(s^{2}+2\unicode[STIX]{x1D701}\unicode[STIX]{x1D714}_{2}s+{\unicode[STIX]{x1D714}_{2}}^{2})}_{\mathit{Helmholtz}}\underbrace{(s^{2}+2\unicode[STIX]{x1D701}\unicode[STIX]{x1D714}_{1}s+{\unicode[STIX]{x1D714}_{1}}^{2})}_{\mathit{Diaphragm}}}. & & \displaystyle\end{eqnarray}$$
Combining (A 2) and (A 5), it can be easily shown that:

Figure 10. Frequency response function of the zero-net-mass-flux (ZNMF) actuator: (a) cavity pressure over driving voltage,
![]() $P_{cav}/V$
; (b) jet velocity over cavity pressure,
$P_{cav}/V$
; (b) jet velocity over cavity pressure,
![]() $U_{jet}/P_{cav}$
.
$U_{jet}/P_{cav}$
.
In figure 10, the frequency response functions (A 6) and (A 5) are plotted. The parameters of the model were determined based on the geometric characteristics of the cavity and orifice and the loudspeaker specifications (table 2). The damping factor of the orifice,
![]() $c$
, is the only parameter that was obtained experimentally. The transfer function was obtained experimentally by exciting the actuator with a broadband frequency signal (white noise) and recording the cavity pressure.
$c$
, is the only parameter that was obtained experimentally. The transfer function was obtained experimentally by exciting the actuator with a broadband frequency signal (white noise) and recording the cavity pressure.
Table 2. Actuator parameters.

Appendix B. Weakly nonlinear analysis
Here, the equations governing the forced amplitude evolution of the unstable global modes of the turbulent flow for the turbulent axisymmetric wake are derived. The analysis is based on the weakly nonlinear analysis proposed by Sipp (Reference Sipp2012), in which the forcing enters the amplitude equations. The analysis distinguishes between two cases depending on the forcing frequency; non-resonant case (
![]() $\unicode[STIX]{x1D714}_{f}$
is not close to
$\unicode[STIX]{x1D714}_{f}$
is not close to
![]() $2\unicode[STIX]{x1D714}_{0}$
) and resonant case (
$2\unicode[STIX]{x1D714}_{0}$
) and resonant case (
![]() $\unicode[STIX]{x1D714}_{f}$
is close to
$\unicode[STIX]{x1D714}_{f}$
is close to
![]() $2\unicode[STIX]{x1D714}_{0}$
).
$2\unicode[STIX]{x1D714}_{0}$
).
B.1 Non-resonant case
B.1.1 Order
 $\sqrt{\unicode[STIX]{x1D700}}^{1}$
$\sqrt{\unicode[STIX]{x1D700}}^{1}$
The above set of equations can also be written in a more elegant way as
with
![]() ${\mathcal{M}}$
being the linearised Navier–Stokes operator,
${\mathcal{M}}$
being the linearised Navier–Stokes operator,
![]() ${\mathcal{P}}$
a prolongation operator which transforms
${\mathcal{P}}$
a prolongation operator which transforms
![]() $\boldsymbol{u}$
into
$\boldsymbol{u}$
into
![]() $(\boldsymbol{u},0)^{\text{T}}$
and
$(\boldsymbol{u},0)^{\text{T}}$
and
![]() ${\mathcal{P}}^{\text{T}}$
a restriction operator which transforms
${\mathcal{P}}^{\text{T}}$
a restriction operator which transforms
![]() $(\boldsymbol{u},p)^{\text{T}}$
quantity into
$(\boldsymbol{u},p)^{\text{T}}$
quantity into
![]() $\boldsymbol{u}$
:
$\boldsymbol{u}$
:
The solution is sought in the form
and consists of the superposition of the global mode and the forcing response. The eigenfunctions
![]() $\boldsymbol{q}_{1}^{A}$
and
$\boldsymbol{q}_{1}^{A}$
and
![]() $\boldsymbol{q}_{1}^{E}$
can be found from:
$\boldsymbol{q}_{1}^{E}$
can be found from:
with
![]() $\boldsymbol{u}=\boldsymbol{u}_{C}$
on some given forcing boundary
$\boldsymbol{u}=\boldsymbol{u}_{C}$
on some given forcing boundary
![]() $\unicode[STIX]{x1D6E4}_{C}$
for (B 6). Equation (B 6) defines
$\unicode[STIX]{x1D6E4}_{C}$
for (B 6). Equation (B 6) defines
![]() $\boldsymbol{q}_{E}$
as the linear response of the flow to the forcing
$\boldsymbol{q}_{E}$
as the linear response of the flow to the forcing
![]() $\boldsymbol{f}_{E}$
. Notice that, in order to invert (B 6), the value
$\boldsymbol{f}_{E}$
. Notice that, in order to invert (B 6), the value
![]() $\text{i}\unicode[STIX]{x1D714}_{f}$
cannot belong to the eigenvalue spectrum at
$\text{i}\unicode[STIX]{x1D714}_{f}$
cannot belong to the eigenvalue spectrum at
![]() $Re_{c}$
.
$Re_{c}$
.
B.1.2 Order
 $\sqrt{\unicode[STIX]{x1D700}}^{2}$
$\sqrt{\unicode[STIX]{x1D700}}^{2}$
Considering equation (B 4), the above system becomes:
 $$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x2202}_{t}{\mathcal{P}}{\mathcal{P}}^{\text{T}}+{\mathcal{M}}\right)\boldsymbol{q}_{2} & = & \displaystyle \boldsymbol{F}_{2}^{1}+|A_{VS}|^{2}\boldsymbol{F}_{2}^{|A_{VS}|^{2}}+[A_{VS}^{2}(\text{e}^{2\text{i}\unicode[STIX]{x1D703}}+\text{e}^{2\text{i}\unicode[STIX]{x1D703}})\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{c}t}\boldsymbol{F}_{2}^{A_{VS}^{2}}+\text{c.c}.]\nonumber\\ \displaystyle & & \displaystyle +\,[A_{VS}E(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{f})t}\boldsymbol{F}_{2}^{A_{VS}E}+A_{VS}E^{\ast }(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{f})t}\boldsymbol{F}_{2}^{A_{VS}E^{\ast }}]\nonumber\\ \displaystyle & & \displaystyle +\,(E^{2}\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{f}t}\boldsymbol{F}_{2}^{E^{2}}+\text{c.c}.)+|E|^{2}\boldsymbol{F}_{2}^{|E|^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x2202}_{t}{\mathcal{P}}{\mathcal{P}}^{\text{T}}+{\mathcal{M}}\right)\boldsymbol{q}_{2} & = & \displaystyle \boldsymbol{F}_{2}^{1}+|A_{VS}|^{2}\boldsymbol{F}_{2}^{|A_{VS}|^{2}}+[A_{VS}^{2}(\text{e}^{2\text{i}\unicode[STIX]{x1D703}}+\text{e}^{2\text{i}\unicode[STIX]{x1D703}})\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{c}t}\boldsymbol{F}_{2}^{A_{VS}^{2}}+\text{c.c}.]\nonumber\\ \displaystyle & & \displaystyle +\,[A_{VS}E(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{f})t}\boldsymbol{F}_{2}^{A_{VS}E}+A_{VS}E^{\ast }(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{f})t}\boldsymbol{F}_{2}^{A_{VS}E^{\ast }}]\nonumber\\ \displaystyle & & \displaystyle +\,(E^{2}\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{f}t}\boldsymbol{F}_{2}^{E^{2}}+\text{c.c}.)+|E|^{2}\boldsymbol{F}_{2}^{|E|^{2}},\end{eqnarray}$$
where
The terms on the right-hand side of (B 8) are forcing terms. The velocity fields involved in these expressions have been determined at lower order. Since (B 8) is linear, we may write the solution as the superposition of
![]() $\boldsymbol{q}_{2}^{1}$
,
$\boldsymbol{q}_{2}^{1}$
,
![]() $\boldsymbol{q}_{2}^{|A|^{2}}$
and
$\boldsymbol{q}_{2}^{|A|^{2}}$
and
![]() $\boldsymbol{q}_{2}^{A^{2}}$
corresponding to the response of the linear system to
$\boldsymbol{q}_{2}^{A^{2}}$
corresponding to the response of the linear system to
![]() $\boldsymbol{F}_{2}^{1}$
,
$\boldsymbol{F}_{2}^{1}$
,
![]() $\boldsymbol{F}_{2}^{|A|^{2}}$
and
$\boldsymbol{F}_{2}^{|A|^{2}}$
and
![]() $\boldsymbol{F}_{2}^{A^{2}}$
, respectively, i.e.
$\boldsymbol{F}_{2}^{A^{2}}$
, respectively, i.e.
 $$\begin{eqnarray}\displaystyle \boldsymbol{q}_{2} & = & \displaystyle \boldsymbol{q}_{2}^{1}+|A_{VS}|^{2}\boldsymbol{q}_{2}^{|A|^{2}}+[A_{VS}^{2}(\text{e}^{2\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-2\text{i}\unicode[STIX]{x1D703}})\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{c}t}\boldsymbol{q}_{2}^{A^{2}}+\text{c.c}.]\nonumber\\ \displaystyle & & \displaystyle +\,[A_{VS}E(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{f})t}\boldsymbol{q}_{2}^{AE}+A_{VS}E^{\ast }(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{f})t}\boldsymbol{q}_{2}^{AE^{\ast }}]\nonumber\\ \displaystyle & & \displaystyle +\,(E^{2}\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{f}t}\boldsymbol{q}_{2}^{E^{2}}+\text{c.c}.)+|E|^{2}\boldsymbol{q}_{2}^{|E|^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q}_{2} & = & \displaystyle \boldsymbol{q}_{2}^{1}+|A_{VS}|^{2}\boldsymbol{q}_{2}^{|A|^{2}}+[A_{VS}^{2}(\text{e}^{2\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-2\text{i}\unicode[STIX]{x1D703}})\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{c}t}\boldsymbol{q}_{2}^{A^{2}}+\text{c.c}.]\nonumber\\ \displaystyle & & \displaystyle +\,[A_{VS}E(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{f})t}\boldsymbol{q}_{2}^{AE}+A_{VS}E^{\ast }(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{f})t}\boldsymbol{q}_{2}^{AE^{\ast }}]\nonumber\\ \displaystyle & & \displaystyle +\,(E^{2}\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{f}t}\boldsymbol{q}_{2}^{E^{2}}+\text{c.c}.)+|E|^{2}\boldsymbol{q}_{2}^{|E|^{2}},\end{eqnarray}$$
where
These are non-degenerate systems that may be readily inverted when the values
![]() $0$
,
$0$
,
![]() $\text{i}(\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x1D714}_{f})$
,
$\text{i}(\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x1D714}_{f})$
,
![]() $\text{i}(\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x1D714}_{f})$
and
$\text{i}(\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x1D714}_{f})$
and
![]() $2\text{i}\unicode[STIX]{x1D714}_{f}$
do not belong to the eigenvalue spectrum. These conditions, together with the one obtained from (B 6), define the resonant cases.
$2\text{i}\unicode[STIX]{x1D714}_{f}$
do not belong to the eigenvalue spectrum. These conditions, together with the one obtained from (B 6), define the resonant cases.
B.1.3 Order
 $\sqrt{\unicode[STIX]{x1D700}}^{3}$
$\sqrt{\unicode[STIX]{x1D700}}^{3}$
The third-order equation is:
Using (B 4) and (B 16), the forcing terms of the right-hand side can be written as
where
Elimination of the secular terms yields the following equation governing the amplitude
![]() $A_{VS}^{\prime }=\sqrt{\unicode[STIX]{x1D700}}A_{VS}$
of the global mode:
$A_{VS}^{\prime }=\sqrt{\unicode[STIX]{x1D700}}A_{VS}$
of the global mode:
B.2 Resonant case
 $\unicode[STIX]{x1D714}_{f}\approx 2\unicode[STIX]{x1D714}_{c}$
$\unicode[STIX]{x1D714}_{f}\approx 2\unicode[STIX]{x1D714}_{c}$
The scaling is
![]() $\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x1D6FA}^{\prime }$
,
$\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x1D714}_{c}+\unicode[STIX]{x1D6FA}^{\prime }$
,
![]() $E^{\prime }=\sqrt{\unicode[STIX]{x1D700}}^{2}E$
,
$E^{\prime }=\sqrt{\unicode[STIX]{x1D700}}^{2}E$
,
![]() $\unicode[STIX]{x1D6FA}^{\prime }=\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FA}$
. At order
$\unicode[STIX]{x1D6FA}^{\prime }=\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FA}$
. At order
![]() $\sqrt{\unicode[STIX]{x1D700}}^{2}$
the solution is sought in the form
$\sqrt{\unicode[STIX]{x1D700}}^{2}$
the solution is sought in the form
 $$\begin{eqnarray}\displaystyle \boldsymbol{q} & = & \displaystyle \boldsymbol{q}_{0}+\sqrt{\unicode[STIX]{x1D700}}[A_{VS}(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}\unicode[STIX]{x1D714}t}\boldsymbol{q}_{1}^{A}+\text{c.c}.]\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{\unicode[STIX]{x1D700}}^{2}[\unicode[STIX]{x1D6FF}\boldsymbol{q}_{2}^{1}+|A_{VS}|^{2}\boldsymbol{q}_{2}^{|A|^{2}}+(A_{VS}^{2}(\text{e}^{2\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-2\text{i}\unicode[STIX]{x1D703}})\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{c}t}\boldsymbol{q}_{2}^{A^{2}}+\text{c.c}.)]\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{\unicode[STIX]{x1D700}}^{2}[E\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{f}t}\boldsymbol{q}_{2}^{E}+\text{c.c}.],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q} & = & \displaystyle \boldsymbol{q}_{0}+\sqrt{\unicode[STIX]{x1D700}}[A_{VS}(\text{e}^{\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-\text{i}\unicode[STIX]{x1D703}})\text{e}^{\text{i}\unicode[STIX]{x1D714}t}\boldsymbol{q}_{1}^{A}+\text{c.c}.]\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{\unicode[STIX]{x1D700}}^{2}[\unicode[STIX]{x1D6FF}\boldsymbol{q}_{2}^{1}+|A_{VS}|^{2}\boldsymbol{q}_{2}^{|A|^{2}}+(A_{VS}^{2}(\text{e}^{2\text{i}\unicode[STIX]{x1D703}}+\text{e}^{-2\text{i}\unicode[STIX]{x1D703}})\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{c}t}\boldsymbol{q}_{2}^{A^{2}}+\text{c.c}.)]\nonumber\\ \displaystyle & & \displaystyle +\,\sqrt{\unicode[STIX]{x1D700}}^{2}[E\text{e}^{2\text{i}\unicode[STIX]{x1D714}_{f}t}\boldsymbol{q}_{2}^{E}+\text{c.c}.],\end{eqnarray}$$
where
The amplitude equation reads