Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-18T21:58:40.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibration of a transversely rotating sphere

Published online by Cambridge University Press:  29 May 2018

Methma M. Rajamuni Open the ORCID record for Methma M. Rajamuni [Opens in a new window] ,
Mark C. Thompson  and
Kerry Hourigan
Methma M. Rajamuni*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of transverse rotation on the vortex-induced vibration (VIV) of a sphere in a uniform flow are investigated numerically. The one degree-of-freedom sphere motion is constrained to the cross-stream direction, with the rotation axis orthogonal to flow and vibration directions. For the current simulations, the Reynolds number of the flow, 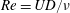$Re=UD/\unicode[STIX]{x1D708}$, and the mass ratio of the sphere, 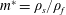$m^{\ast }=\unicode[STIX]{x1D70C}_{s}/\unicode[STIX]{x1D70C}_{f}$, were fixed at 300 and 2.865, respectively, while the reduced velocity of the flow was varied over the range 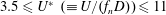$3.5\leqslant U^{\ast }~(\equiv U/(f_{n}D))\leqslant 11$, where, 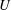$U$ is the upstream velocity of the flow, 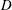$D$ is the sphere diameter, $\unicode[STIX]{x1D708}$ is the fluid viscosity, 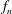$f_{n}$ is the system natural frequency and 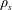$\unicode[STIX]{x1D70C}_{s}$ and 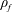$\unicode[STIX]{x1D70C}_{f}$ are solid and fluid densities, respectively. The effect of sphere rotation on VIV was studied over a wide range of non-dimensional rotation rates: 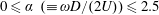$0\leqslant \unicode[STIX]{x1D6FC}~(\equiv \unicode[STIX]{x1D714}D/(2U))\leqslant 2.5$, with 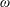$\unicode[STIX]{x1D714}$ the angular velocity. The flow satisfied the incompressible Navier–Stokes equations while the coupled sphere motion was modelled by a spring–mass–damper system, under zero damping. For zero rotation, the sphere oscillated symmetrically through its initial position with a maximum amplitude of approximately 0.4 diameters. Under forced rotation, it oscillated about a new time-mean position. Rotation also resulted in a decreased oscillation amplitude and a narrowed synchronisation range. VIV was suppressed completely for 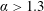$\unicode[STIX]{x1D6FC}>1.3$. Within the 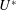$U^{\ast }$ synchronisation range for each rotation rate, the drag force coefficient increased while the lift force coefficient decreased from their respective pre-oscillatory values. The increment of the drag force coefficient and the decrement of the lift force coefficient reduced with increasing reduced velocity as well as with increasing rotation rate. In terms of wake dynamics, in the synchronisation range at zero rotation, two equal-strength trails of interlaced hairpin-type vortex loops were formed behind the sphere. Under rotation, the streamwise vorticity trail on the advancing side of the sphere became stronger than the trail in the retreating side, consistent with wake deflection due to the Magnus effect. This symmetry breaking appears to be associated with the reduction in the observed amplitude response and the narrowing of the synchronisation range. In terms of variation with Reynolds number, the sphere oscillation amplitude was found to increase over the range 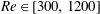$Re\in [300,1200]$ at 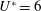$U^{\ast }=6$ for each of 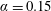$\unicode[STIX]{x1D6FC}=0.15$, 0.75 and 1.5. The VIV response depends strongly on Reynolds number, with predictions indicating that VIV will persist for higher rotation rates at higher Reynolds numbers.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 786 - 820
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16 (1), 195–222.CrossRefGoogle Scholar
Behara, S., Borazjani, I. & Sotiropoulos, F. 2011 Vortex-induced vibrations of an elastically mounted sphere with three degrees of freedom at Re = 300: hysteresis and vortex shedding modes. J. Fluid Mech. 686, 426–450.CrossRefGoogle Scholar
Behara, S. & Sotiropoulos, F. 2016 Vortex-induced vibrations of an elastically mounted sphere: the effects of Reynolds number and reduced velocity. J. Fluids Struct. 66, 54–68.CrossRefGoogle Scholar
Blackburn, H. & Henderson, R. 1996 Lock-in behavior in simulated vortex-induced vibration. Exp. Therm. Fluid Sci. 12 (2), 184–189.CrossRefGoogle Scholar
Bourguet, R. & Jacono, D. L. 2014 Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 740, 342–380.CrossRefGoogle Scholar
Dobson, J., Ooi, A. & Poon, E. K. W. 2014 The flow structures of a transversely rotating sphere at high rotation rates. Comput. Fluids 102, 170–181.CrossRefGoogle Scholar
Giacobello, M., Ooi, A. & Balachandar, S. 2009 Wake structure of a transversely rotating sphere at moderate Reynolds numbers. J. Fluid Mech. 621, 103–130.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C. H. K. 1997 Vortex-induced motions of a tethered sphere. J. Wind Engng Ind. Aerodyn. 69, 375–385.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Govardhan, R. N. & Williamson, C. H. K. 2005 Vortex-induced vibrations of a sphere. J. Fluid Mech. 531, 11–47.CrossRefGoogle Scholar
Hout, R. V., Katz, A. & Greenblatt, D. 2013 Time-resolved particle image velocimetry measurements of vortex and shear layer dynamics in the near wake of a tethered sphere. Phys. Fluids 25 (7), 077102.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, vol. 2, pp. 193–208. Stanford University.Google Scholar
Issa, R. I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62 (1), 40–65.CrossRefGoogle Scholar
Jasak, H. & Tukovic, Z. 2010 Dynamic mesh handling in Openfoam applied to fluid-structure interaction simulations. In Proceedings of the V European Conference on Computational Fluid Dynamics: ECCOMAS CFD 2010, Lisbon, Portugal (ed. Pereira, J. C. F., Sequeira, A. & Pereira, J. M. C.), ECCOMAS.Google Scholar
Jauvtis, N., Govardhan, R. & Williamson, C. H. K. 2001 Multiple modes of vortex-induced vibration of a sphere. J. Fluids Struct. 15 (3), 555–563.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kim, D. 2009 Laminar flow past a sphere rotating in the transverse direction. J. Mech. Sci. Technol. 23 (2), 578–589.CrossRefGoogle Scholar
Krakovich, A., Eshbal, L. & Hout, R. V. 2013 Vortex dynamics and associated fluid forcing in the near wake of a light and heavy tethered sphere in uniform flow. Exp. Fluids 54 (11), 1615.CrossRefGoogle Scholar
Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.CrossRefGoogle Scholar
Lee, H., Hourigan, K. & Thompson, M. C. 2013 Vortex-induced vibration of a neutrally buoyant tethered sphere. J. Fluid Mech. 719, 97–128.CrossRefGoogle Scholar
Lee, H., Thompson, M. C. & Hourigan, K. 2008 Flow around a tethered neutrally-buoyant sphere. In Proceedings of the XXII International Congress of Theoretical and Applied Mechanics, Adelaide Convention Centre, Adelaide, Australia (ed. Denier, J., Finn, M. & Mattner, T.), International Union of Theoretical and Applied Mechanics.Google Scholar
Leontini, J. S., Stewart, B. E., Thompson, M. C. & Hourigan, K. 2006a Predicting vortex-induced vibration from driven oscillation results. Appl. Math. Model. 30 (10), 1096–1102.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006b The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22 (6), 857–864.CrossRefGoogle Scholar
Lighthill, J. 1986 Wave loading on offshore structures. J. Fluid Mech. 173, 667–681.CrossRefGoogle Scholar
Magnus, G. 1853 Über die Abweichung der Geschosse, und: Über eine abfallende Erscheinung bei rotierenden Körpern, vol. 164. Annalen der Physik.Google Scholar
Naudascher, E. & Rockwell, D. 2012 Flow-induced Vibrations: an Engineering Guide. Courier Corporation.Google Scholar
Parkinson, G. 1989 Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 26 (2), 169–224.CrossRefGoogle Scholar
Poon, E. K. W., Ooi, A. S. H., Giacobello, M. & Cohen, R. C. Z. 2010 Laminar flow structures from a rotating sphere: effect of rotating axis angle. Intl J. Heat Fluid Flow 31 (5), 961–972.CrossRefGoogle Scholar
Poon, E. K. W., Ooi, A. S. H., Giacobello, M., Iaccarino, G. & Chung, D. 2014 Flow past a transversely rotating sphere at Reynolds numbers above the laminar regime. J. Fluid Mech. 759, 751–781.CrossRefGoogle Scholar
Pregnalato, C. J.2003 Flow-induced vibrations of a tethered sphere. PhD, Monash University.Google Scholar
Rajamuni, M. M., Thompson, M. C. & Hourigan, K. 2018 Transverse flow-induced vibrations of a sphere. J. Fluid Mech. 837, 931–966.CrossRefGoogle Scholar
Robins, B. 1972 New Principle of Gunnery (of 1742). Republished by Richmond Publishing.Google Scholar
Rubinow, S. I. & Keller, J. B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11 (03), 447–459.CrossRefGoogle Scholar
Sareen, A., Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018 Vortex-induced vibration of a rotating sphere. J. Fluid Mech. 837, 258–292.CrossRefGoogle Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Seyed-Aghazadeh, B. & Modarres-Sadeghi, Y. 2015 An experimental investigation of vortex-induced vibration of a rotating circular cylinder in the crossflow direction. Phys. Fluids 27 (6), 067101.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 1997 Dynamics and forcing of a tethered sphere in a fluid flow. J. Fluids Struct. 11 (3), 293–305.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2008 A brief review of recent results in vortex-induced vibrations. J. Wind Engng Ind. Aerodyn. 96 (6), 713–735.CrossRefGoogle Scholar
Wong, K. W., Zhao, J., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2017 Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 829, 486–511.CrossRefGoogle Scholar
Wu, X., Ge, F. & Hong, Y. 2012 A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluids Struct. 28, 292–308.CrossRefGoogle Scholar