Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-19T06:08:36.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional wake transition of a diamond-shaped cylinder

Published online by Cambridge University Press:  14 May 2021

Hongyi Jiang Open the ORCID record for Hongyi Jiang [Opens in a new window]
Hongyi Jiang*
Affiliation:
School of Engineering, The University of Western Australia, 35 Stirling Highway, Perth, WA6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

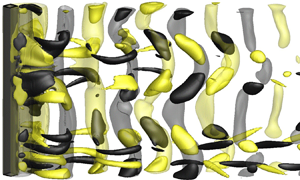
Three-dimensional (3-D) wake transition for flow past a diamond cylinder is investigated numerically. Detailed 3-D direct numerical simulations (DNS) show that the wake is represented by mode A with global vortex dislocations for Reynolds numbers Re = 121–150, followed by a mode swapping between modes A and B for Re = 160–210 and increasingly disordered mode B for Re ≥ 220. In the mode swapping regime, different characteristics of the dislocation and non-dislocation periods are revealed by decomposing flow properties (e.g. the root-mean-square lift coefficient) into the values corresponding to the dislocation and non-dislocation periods. Such decomposition helps to explain some major differences observed for the cases of a diamond and a circular cylinder. In addition to DNS, Floquet stability analyses are conducted to identify the 3-D wake instability modes of a diamond cylinder up to Re = 300. Phase-averaged base flow is used to eliminate the quantitative uncertainties induced by the aperiodic secondary vortex street of the base flow. Interestingly, a subharmonic instability mode is identified at Re ≥ 285, whereas mode B is absent. The origin of the subharmonic mode is explained. The disagreement between the DNS and the Floquet analysis regarding the existence of mode B and the subharmonic mode is also explained. It is found that the natural 3-D flow involves complex interactions between the streamwise and spanwise vortices, as well as between the 3-D wake transition and the two-dimensional base-flow transition, which excite mode B and suppress the subharmonic mode.

JFM classification

Wakes/Jets: Wakes Vortex Flows: Vortex instability Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 918 , 10 July 2021 , A35
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akbar, T., Bouchet, G. & Dušek, J. 2011 Numerical investigation of the subcritical effects at the onset of three-dimensionality in the circular cylinder wake. Phys. Fluids 23, 094103.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Barkley, D., Tuckerman, L.S. & Golubitsky, M. 2000 Bifurcation theory for three-dimensional flow in the wake of a circular cylinder. Phys. Rev. E 61, 5247–5252.CrossRefGoogle ScholarPubMed
Blackburn, H.M. & Lopez, J.M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.CrossRefGoogle Scholar
Blackburn, H.M. & Sheard, G.J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22, 031701.CrossRefGoogle Scholar
Cantwell, C.D., et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Carmo, B.S., Meneghini, J.R. & Sherwin, S.J. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
Choi, C., Jang, Y. & Yang, K. 2012 Secondary instability in the near-wake past two tandem square cylinders. Phys. Fluids 24, 024102.CrossRefGoogle Scholar
Henderson, R.D. 1995 Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7, 2102–2104.CrossRefGoogle Scholar
Henderson, R.D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Henderson, R.D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8, 1683–1685.CrossRefGoogle Scholar
Issa, R.I. 1986 Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2017 Strouhal–Reynolds number relationship for flow past a circular cylinder. J. Fluid Mech. 832, 170–188.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2018 Hydrodynamic characteristics of flow past a square cylinder at moderate Reynolds numbers. Phys. Fluids 30, 104107.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2019 Transition to the secondary vortex street in the wake of a circular cylinder. J. Fluid Mech. 867, 691–722.CrossRefGoogle Scholar
Jiang, H., Cheng, L. & An, H. 2017 a On numerical aspects of simulating flow past a circular cylinder. Intl J. Numer. Meth. Fluids 85, 113–132.CrossRefGoogle Scholar
Jiang, H., Cheng, L. & An, H. 2018 a Three-dimensional wake transition of a square cylinder. J. Fluid Mech. 842, 102–127.CrossRefGoogle Scholar
Jiang, H., Cheng, L., An, H., Tong, F. & Yang, F. 2018 b. Flow past a diamond cylinder at moderate Reynolds numbers. In 21st Australasian Fluid Mechanics Conference, Adelaide, Australia.Google Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017 b Prediction of the secondary wake instability of a circular cylinder with direct numerical simulation. Comput. Fluids 149, 172–180.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.CrossRefGoogle Scholar
Karniadakis, G.E. & Sherwin, S.J. 2005 Spectral/hp Element Methods for CFD. Oxford University Press.Google Scholar
Leweke, T. & Williamson, C.H.K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.CrossRefGoogle Scholar
Ng, Z.Y., Vo, T., Hussam, W.K. & Sheard, G.J. 2016 Two-dimensional wake dynamics behind cylinders with triangular cross-section under incidence angle variation. J. Fluids Struct. 63, 302–324.CrossRefGoogle Scholar
Park, D. & Yang, K. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Posdziech, O. & Grundmann, R. 2001 Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 15, 121–141.Google Scholar
Robichaux, J., Balachandar, S. & Vanka, S.P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11, 560–578.CrossRefGoogle Scholar
Saha, A.K. 2007 Far-wake characteristics of two-dimensional flow past a normal flat plate. Phys. Fluids 19, 128110.CrossRefGoogle Scholar
Serson, D., Meneghini, J.R., Carmo, B.S., Volpe, E.V. & Gioria, R.S. 2014 Wake transition in the flow around a circular cylinder with a splitter plate. J. Fluid Mech. 755, 582–602.CrossRefGoogle Scholar
Sheard, G.J., Fitzgerald, M.J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.CrossRefGoogle Scholar
Sheard, G.J., Thompson, M.C. & Hourigan, K. 2003 A coupled Landau model describing the Strouhal–Reynolds number profile of a three-dimensional circular cylinder wake. Phys. Fluids 15, L68–L71.CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11, 288–306.CrossRefGoogle Scholar
Thompson, M.C., Leweke, T. & Williamson, C.H.K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Thompson, M.C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.CrossRefGoogle Scholar
Tong, X.H., Luo, S.C. & Khoo, B.C. 2008 Transition phenomena in the wake of an inclined square cylinder. J. Fluids Struct. 24, 994–1005.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Yildirim, I., Rindt, C.C.M. & van Steenhoven, A.A. 2013 Energy contents and vortex dynamics in Mode-C transition of wired-cylinder wake. Phys. Fluids 25, 054103.CrossRefGoogle Scholar
Yoon, D., Yang, K. & Choi, C. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22, 043603.CrossRefGoogle Scholar
Yoon, D., Yang, K. & Choi, C. 2012 Three-dimensional wake structures and aerodynamic coefficients for flow past an inclined square cylinder. J. Wind Engng Ind. Aerodyn. 101, 34–42.CrossRefGoogle Scholar