Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-03T05:14:47.473Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of the wakes of cylinders with triangular cross-sections

Published online by Cambridge University Press:  12 April 2018

Zhi Y. Ng Open the ORCID record for Zhi Y. Ng [Opens in a new window] ,
Tony Vo  and
Gregory J. Sheard Open the ORCID record for Gregory J. Sheard [Opens in a new window]
Zhi Y. Ng
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Tony Vo
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Gregory J. Sheard*
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of the wakes of cylinders with triangular cross-sections at incidence is investigated using Floquet stability analysis to elucidate the effects of cylinder inclination on the dominant flow instability. The upper limit of the Reynolds numbers (scaled by the height projected by the cylinder in this study) at which the wake of the two-dimensional base flow is time periodic is 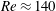$Re\approx 140$ for most cylinder inclinations, exceeding which the flow becomes aperiodic, restricting the range of Reynolds numbers permitted for the stability analysis. Two different instability modes are predicted to manifest as the first-occurring mode at various cylinder inclinations – a regular mode possessing perturbation structures consistent with mode A dominates the wakes of cylinders at inclinations 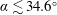$\unicode[STIX]{x1D6FC}\lesssim 34.6^{\circ }$ and 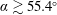$\unicode[STIX]{x1D6FC}\gtrsim 55.4^{\circ }$, with a subharmonic mode consistent with mode C emerging as the primary mode in the wakes of the cylinder at the intermediate range of inclinations. For all inclinations, the mode B branch is not detected within the range of Reynolds numbers examined. The peak instability growth rates corresponding to mode A for all cylinder inclinations describe a linear variation with 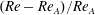$(Re-Re_{A})/Re_{A}$, where 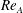$Re_{A}$ is the mode A transition Reynolds number, while those corresponding to mode C vary only approximately linearly. The generalized trend most pertinently shows mode C to develop more rapidly than mode A at inclinations which permit it. Examination of the near wake of the two-dimensional time-periodic base flow demonstrates the dependence of the development and intensity of mode C on imbalances in the flow solution over each shedding period, directly implying that the two-dimensional base flow solutions deviate from the half-period-flip map as the cylinder inclination is increased. The degree of asymmetry of the two-dimensional base flow relative to the ideal half-period-flip map is quantified using several measures. The results show distinctly different trends in these asymmetry measures between inclinations where modes A or C are dominant, agreeing with results from the stability analysis. The nature of the predicted instability modes at transition are also investigated by applying the Stuart–Landau equation, showing the transitions to be supercritical for all cylinder inclinations, with mode C being consistently more strongly supercritical than mode A.

JFM classification

Instability: Instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 721 - 745
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bao, Y., Zhou, D. & Zhao, Y.-J. 2010 A two-step Taylor-characteristic-based Galerkin method for incompressible flows and its application to flow over triangular cylinder with different incidence angles. Intl J. Numer. Meth. Fluids 62 (11), 1181–1208.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.10.1017/S0022112096002777Google Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15 (8), L57–L60.10.1063/1.1591771Google Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.10.1017/S0022112004002095Google Scholar
Blackburn, H. M. & Sheard, G. J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701.10.1063/1.3368106Google Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element-Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.10.1016/j.jcp.2004.02.013Google Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.10.1017/S0022112009992473Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.10.1017/S0022112007009639Google Scholar
De, A. K. & Dalal, A. 2006 Numerical simulation of unconfined flow past a triangular cylinder. Intl J. Numer. Meth. Fluids 52 (7), 801–821.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.10.1017/CBO9780511616938Google Scholar
Gerrard, J. H. 1978 The wakes of cylindrical bluff bodies at low Reynolds number. Phil. Trans. R. Soc. Lond. A 288 (1354), 351–382.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.10.1017/S0022112097007465Google Scholar
Henderson, R. D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8 (6), 1683–1685.10.1063/1.868939Google Scholar
Iungo, G. V. & Buresti, G. 2009 Experimental investigation on the aerodynamic loads and wake flow features of low aspect-ratio triangular prisms at different wind directions. J. Fluids Struct. 25 (7), 1119–1135.10.1016/j.jfluidstructs.2009.06.004Google Scholar
Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.10.1017/S0022112087002234Google Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017 Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall. J. Fluid Mech. 812, 435–462.10.1017/jfm.2016.810Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.10.1016/0021-9991(91)90007-8Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.10.1017/S0022112092001617Google Scholar
Landau, L. D. & Lifshitz, E. M. 1976 Mechanics, 3rd edn. Pergamon Press.Google Scholar
Lehoucq, R., Sorensen, D. & Yang, C. 1998 ARPACK Users’ Guide. Society for Industrial and Applied Mathematics.10.1137/1.9780898719628Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2015 Stability analysis of the elliptic cylinder wake. J. Fluid Mech. 763, 302–321.10.1017/jfm.2014.671Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17 (4), 571–586.10.1016/S0997-7546(98)80012-5Google Scholar
Luo, S. C. & Eng, G. R. C. 2010 Discontinuities in the S - Re relations of trapezoidal and triangular cylinders. Proc. SPIE 7522, 75221B.Google Scholar
Marques, F., Lopez, J. M. & Blackburn, H. M. 2004 Bifurcations in systems with Z 2 spatio-temporal and O (2) spatial symmetry. Physica D 189, 247–276.Google Scholar
Mathis, C., Provansal, M. & Boyer, L. 1984 The Benard–Von Karman instability: an experimental study near the threshold. J. Phys. Lett. 45 (10), 483–491.10.1051/jphyslet:019840045010048300Google Scholar
Monkewitz, P. A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds numbers. Phys. Fluids 31 (5), 999–1006.10.1063/1.866720Google Scholar
Ng, Z. Y., Vo, T., Hussam, W. K. & Sheard, G. J. 2016 Two-dimensional wake dynamics behind cylinders with triangular cross-section under incidence angle variation. J. Fluids Struct. 63, 302–324.10.1016/j.jfluidstructs.2016.04.003Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.10.1017/S0022112087002222Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013 Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.10.1017/jfm.2012.542Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2017 Three-dimensionality of elliptical cylinder wakes at low angles of incidence. J. Fluid Mech. 825, 245–283.10.1017/jfm.2017.366Google Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.10.1063/1.869930Google Scholar
Ryan, K., Butler, C. J. & Sheard, G. J. 2012 Stability characteristics of a counter-rotating unequal-strength Batchelor vortex pair. J. Fluid Mech. 696, 374–401.10.1017/jfm.2012.55Google Scholar
Sapardi, A. M., Hussam, W. K., Pothérat, A. & Sheard, G. J. 2017 Linear stability of confined flow around a 180-degree sharp bend. J. Fluid Mech. 822, 813–847.10.1017/jfm.2017.266Google Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27 (5–6), 734–742.10.1016/j.jfluidstructs.2011.02.005Google Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.10.1017/S0022112009006879Google Scholar
Sheard, G. J., Leweke, T., Thompson, M. C. & Hourigan, K. 2007 Flow around an impulsively arrested circular cylinder. Phys. Fluids 19 (8), 083601.10.1063/1.2754346Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.10.1017/S0022112003005512Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 Asymmetric structure and non-linear transition behaviour of the wakes of toroidal bodies. Eur. J. Mech. (B/Fluids) 23 (1), 167–179.10.1016/j.euromechflu.2003.04.005Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005a Subharmonic mechanism of the mode C instability. Phys. Fluids 17 (11), 111702.10.1063/1.2139682Google Scholar
Sheard, G. J., Thompson, M. C., Hourigan, K. & Leweke, T. 2005b The evolution of a subharmonic mode in a vortex street. J. Fluid Mech. 534, 23–38.10.1017/S0022112005004313Google Scholar
Sreenivasan, K. R., Strykowski, P. J. & Olinger, D. J. 1987 Hopf bifurcation, Landau equation, and vortex shedding behind circular cylinders. In Proceedings of the Forum on Unsteady Flow Separation (ed. Ghia, K. N.), vol. 52, pp. 1–13. American Society of Mechanical Engineers.Google Scholar
Thompson, M., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12 (2), 190–196.10.1016/0894-1777(95)00098-4Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15 (3–4), 607–616.10.1006/jfls.2000.0369Google Scholar
Thompson, M. C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.10.1017/jfm.2014.314Google Scholar
Tu, J., Zhou, D., Bao, Y., Han, Z. & Li, R. 2014 Flow characteristics and flow-induced forces of a stationary and rotating triangular cylinder with different incidence angles at low Reynolds numbers. J. Fluids Struct. 45, 107–123.10.1016/j.jfluidstructs.2013.11.004Google Scholar
Vo, T., Montabone, L., Read, P. L. & Sheard, G. J. 2015 Non-axisymmetric flows in a differential-disk rotating system. J. Fluid Mech. 775, 349–386.10.1017/jfm.2015.270Google Scholar
Williamson, C. H. K. 1988a Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.10.1063/1.866978Google Scholar
Williamson, C. H. K. 1988b The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.10.1063/1.866925Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.10.1017/S0022112096008750Google Scholar
Yang, D., Pettersen, B., Andersson, H. I. & Narasimhamurthy, V. D. 2013 Floquet stability analysis of the wake of an inclined flat plate. Phys. Fluids 25 (9), 094103.10.1063/1.4820815Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013a Energy contents and vortex dynamics in Mode-C transition of wired-cylinder wake. Phys. Fluids 25, 054103.10.1063/1.4801849Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013b Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.10.1017/jfm.2013.230Google Scholar
Yoon, D.-H., Yang, K.-S. & Choi, C.-B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22 (4), 043603.10.1063/1.3388857Google Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.10.1063/1.868601Google Scholar
Zielinska, B. J. A. & Wesfreid, J. E. 1995 On the spatial structure of global modes in wake flow. Phys. Fluids 7 (6), 1418–1424.10.1063/1.868529Google Scholar