Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-17T22:37:54.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Spinning detonation, cross-currents, and the Chapman–Jouguet velocity

Published online by Cambridge University Press:  04 September 2014

M. Kurosaka  and
N. Tsuboi
M. Kurosaka*
Affiliation:
William E. Boeing Department of Aeronautics & Astronautics, University of Washington, Seattle, WA 98195-2400, USA
N. Tsuboi
Affiliation:
Department of Mechanical & Control Engineering, Kyushu Institute of Technology, Kitakyushu, Fukuoka, 804-8550, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Interestingly, the Chapman–Jouguet detonation velocity (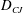$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D_{CJ}$) based on a one-dimensional and steady model compares well with the measured data. For the spinning detonation, in particular, this agreement is particularly notable, since the flow is highly three-dimensional and unsteady; perpendicular to the leading shock front, a transverse detonation wave (TDW) spins periodically. In the wake of this TDW, a secondary flow, called here the cross-current, appears which is orthogonal to the leading shock. Despite the presence of these cross-currents, the 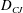$D_{CJ}$ agreement remains remarkably satisfactory, and we investigate the reason for this, for spinning detonation in a tube. First, we focus on the origin of the cross-current. The cross-current, driven by the shock pressure, arises initially across a warped shock frontal surface, and both its sign and magnitude depend on the local slopes of the shock surface. The cross-current undergoes further pressure-driven transitions, with its magnitude eventually diminishing downstream and reducing the flow to a quasi-one-dimensional one. Second, regarding the unsteadiness, under the assumptions that the TDW spins at constant angular wave speed and the flow is steady in the frame rotating with it, the unsteady energy equation becomes integrable, resulting in the invariance of the so-called rothalpy. Also, in the integral forms of the mass and momentum balance, the unsteady terms drop out. Taken together, in the far field the governing equations are reduced to being one-dimensional and steady. From these the 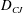$D_{CJ}$ follows immediately, which appears to be the reason for the enduring usefulness of the 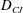$D_{CJ}$. The results of the analysis are confirmed with computational fluid dynamics (CFD). Additionally, the area-averaged flow profiles are found to display more than a passing resemblance to the Zeldovitch–Von Neumann–Doering (ZND) model.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Detonation waves Reacting Flows: Reacting Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 728 - 757
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aslam, T. D.1996 Investigations on detonation shock dynamics. PhD thesis, University of Illinois, Urbana-Champaign.Google Scholar
Bdzil, J. B. & Stewart, D. S. 1989 Modeling of two-dimensional detonation with detonation shock dynamics. Phys. Fluids A 1, 1261–1287.Google Scholar
Chapman, D. L. 1889 On the rate of explosion in gases. Phil. Mag. 47, 90–104.Google Scholar
Cumpsty, N. A. 1989 Compressor Aerodynamics. Longman Scientific and Technical.Google Scholar
Gamezo, V. N., Desbordes, D. & Oran, E. S. 1999 Two-dimensional reactive flow dynamics in cellular detonation waves. Shock Waves 9, 11–17.CrossRefGoogle Scholar
Greitzer, E. M., Tan, C. S. & Graf, M. B. 2004 Internal Flow: Concepts and Applications. Cambridge University Press.Google Scholar
Jouguet, J. C. E. 1905 Sur la propagation des réactions chimiques dans les gaz. J. Math. Pures Appl. 2, 5–86.Google Scholar
Kurosaka, M. & Sundram, P. 1986 Illustrative examples of streaklines in unsteady vortices: interpretational difficulties revisited. Phys. Fluids 29, 3474–3477.Google Scholar
Lee, J. H. S. 2008 The Detonation Phenomenon. Cambridge University Press.Google Scholar
LeVeque, R. J. 1992 Numerical Methods for Conservation Laws. Birkhäuser.Google Scholar
Nikolaev, Y. A. & Zak, D. V. 1989 Quasi-one-dimensional model of self-sustaining multi front gas detonation with losses and turbulence taken into account. Combust. Explosions Shock Waves 25, 225–233.CrossRefGoogle Scholar
Nonomura, T., Iizuka, N. & Fujii, K. 2010 Freestream and vortex preservation properties of high-order WENO and WCNS on curvilinear grids. Comput. Fluids 39, 197–214.Google Scholar
Petersen, E. L. & Hanson, R. K. 1999 Reduced kinetics mechanisms for Ram accelerator combustion. J. Propul. Power 15, 591–600.Google Scholar
Radulescu, M. I., Sharpe, G. L., Law, C. K. & Lee, J. H. S. 2007 The hydrodynamic structure of unstable cellular detonations. J. Fluid Mech. 580, 31–81.Google Scholar
Schott, G. L. 1965 Observation of the structure of spinning detonation. Phys. Fluids 8, 850–865.Google Scholar
Shuen, J. S. 1992 Upwind differencing and lu factorization for chemical non-equilibrium Navier–Stokes equations. J. Comput. Phys. 99, 233–250.CrossRefGoogle Scholar
Stewart, D. S. & Bdzil, J. B. 1988 The shock dynamics of stable multidimensional detonation. Combust. Flame 72, 311–323.Google Scholar
Strehlow, R. A. 1988 Combustion Fundamentals. McGraw-Hill.Google Scholar
Tsuboi, N., Eto, K. & Hayashi, A. K. 2007a Detailed structure of spinning detonation in a circular tube. Combust. Flame 149, 144–161.Google Scholar
Tsuboi, N. & Hayashi, A. K. 2007b Numerical study on spin detonation. Proc. Combust. Inst. 31, 2389–2396.Google Scholar
Tsuboi, N., Hayashi, A. K. & Koshi, M. 2008 Energy release effect of mixture on single spinning detonation structure. Proc. Combust. Inst. 32, 2405–2412.CrossRefGoogle Scholar
Virot, F., Kurosaka, M., Khasainov, B., Desbordes, D. & Presles, H. N. 2008 Flow reversal in spinning detonation. In 17th International Symposium on Hazards, Prevention, and Mitigation of Industrial Explosions Conference, St. Petersburg, Russia, July 11th, 2008.Google Scholar
Voytsekhovskiy, B. V., Mitrofanov, V. V. & Topchian, M. Ye.1963 The structure of detonation front in gases. Tech. Rep. FTD-MT-64-527 (translated by Air Force Systems Command, Wright-Patterson Air Force Base, Dayton, OH).Google Scholar
Wada, Y. & Liou, M. S.1994 A flux-splitting scheme with high-resolution and robustness for discontinuities. AIAA Paper 94-0083.Google Scholar
White, D. R. 1961 Turbulent structure of gaseous detonation. Phys. Fluids 4, 465–480.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. John Wiley and Sons.Google Scholar
Williams, F. A. 1985 Combustion Theory, 2nd edn Benjamin/Cummings.Google Scholar
Wu, C. H.1952 A general theory of three-dimensional flow in subsonic and supersonic turbomachines of axial-, radial-, and mixed-flow types. NACA TN 2604.Google Scholar
Yao, J. & Stewart, D. S. 1996 On the dynamics of multi-dimensional detonation. J. Fluid Mech. 309, 225–275.CrossRefGoogle Scholar