Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T06:47:10.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Reflection of oscillating internal shear layers: nonlinear corrections

Published online by Cambridge University Press:  23 July 2020

Stéphane Le Dizès Open the ORCID record for Stéphane Le Dizès [Opens in a new window]
Stéphane Le Dizès*
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, UMR 7342, 13384Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

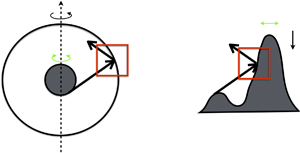
In this work, we perform weakly nonlinear analysis of the reflection process of a thin oscillating wave beam on a non-critical surface in a fluid rotating and stratified along the same vertical axis in the limit of weak viscosity, i.e. small Ekman number $E$. We assume that the beam has the self-similar viscous structure obtained by Moore & Saffman (Phil. Trans. R. Soc. A, vol. 264, 1969, pp. 597–634) and Thomas & Stevenson (J. Fluid Mech., vol. 54, 1972, pp. 495–506). Such a solution describes the viscous internal shear layers of width $O(E^{1/3})$ generated by a localized oscillating source. We first show that the reflected beam conserves at leading order the self-similar structure of the incident beam and is modified by an $O(E^{1/6})$ correction with a different self-similar structure. We then analyse the nonlinear interaction of the reflected beam with the incident beam of amplitude $\varepsilon$ and demonstrate that a second-harmonic beam and localized meanflow correction, both of amplitude $\varepsilon ^{2} E^{-1/3}$, are created. We further show that for the purely stratified case (respectively the purely rotating case), a non-localized meanflow correction of amplitude $\varepsilon ^{2} E^{-1/6}$ is generated, except when the boundary is horizontal (respectively vertical). In this latter case, the meanflow correction remains localized but exhibits a triple-layer structure with a large $O(E^{4/9})$ viscous layer.

JFM classification

Boundary Layers: Boundary layer separation Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , A21
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balmforth, N. & Peacock, T. 2009 Tidal conversion by supercritical topography. J. Phys. Oceanogr. 39 (8), 1965–1974.CrossRefGoogle Scholar
Beckebanze, F., Brouzet, C., Sibgatullin, I. N. & Maas, L. R. M. 2018 Damping of quasi-two-dimensional internal wave attractors by rigid-wall friction. J. Fluid Mech. 841, 615–635.CrossRefGoogle Scholar
Bordes, G., Venaille, A., Joubaud, S., Odier, P. & Dauxois, T. 2012 Experimental observation of a strong mean flow induced by internal gravity waves. Phys. Fluids 24, 086602.CrossRefGoogle Scholar
Bretherton, F. P. 1969 On the mean motion induced by internal gravity waves. J. Fluid Mech. 36, 785–803.CrossRefGoogle Scholar
Busse, F. 1968 Steady fluid flow in a precessing spheroidal shell. J. Fluid Mech. 33, 739–751.CrossRefGoogle Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.CrossRefGoogle Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602.CrossRefGoogle Scholar
Cébron, D., Laguerre, R., Noir, J. & Schaeffer, N. 2019 Precessing spherical shells: flows, dissipation, dynamo and the lunar core. Geophys. J. Intl 219, S34–S57.CrossRefGoogle Scholar
Cortet, P.-P., Lamriben, C. & Moisy, F. 2010 Viscous spreading of an inertial wave beam in a rotating fluid. Phys. Fluids 22, 086603.CrossRefGoogle Scholar
Dauxois, T., Joubaud, S., Odier, P. & Venaille, A. 2018 Instabilities of internal gravity wave beams. Annu. Rev. Fluid Mech. 50, 1–28.CrossRefGoogle Scholar
Dauxois, T. & Young, W. R. 1999 Near-critical reflection of internal waves. J. Fluid Mech. 390, 271–295.CrossRefGoogle Scholar
Davis, R. E. & Acrivos, A. 1967 The stability of oscillatory internal waves. J. Fluid Mech. 30, 723–736.CrossRefGoogle Scholar
Echeverri, P. & Peacock, T. 2010 Internal tide generation by arbitrary two-dimensional topography. J.Fluid Mech. 659, 247–266.CrossRefGoogle Scholar
Favier, B., Barker, A. J., Baruteau, C. & Ogilvie, G. I. 2014 Non-linear evolution of tidally forced inertial waves in rotating fluid bodies. Mon. Not. R. Astron. Soc. 439, 845–860.CrossRefGoogle Scholar
Gostiaux, L., Dauxois, T., Didelle, H., Sommeria, J. & Viboud, S. 2006 Quantitative laboratory observations of internal wave reflection on ascending slopes. Phys. Fluids 18, 056602.CrossRefGoogle Scholar
Grisouard, N., Staquet, C. & Pairaud, I. 2015 Numerical simulation of a two-dimensional internal wave atractor. J. Fluid Mech. 614, 1–14.CrossRefGoogle Scholar
Hollerbach, R. & Kerswell, R. 1995 Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 298, 327–339.CrossRefGoogle Scholar
Jiang, C.-H. & Marcus, P. S. 2009 Selection rules for the nonlinear interaction of internal gravity waves. Phys. Rev. Lett. 102, 124502.CrossRefGoogle ScholarPubMed
Kataoka, T. & Akylas, T. R. 2015 On three-dimensional internal gravity wave beams and induced large-scale mean flows. J. Fluid Mech. 769, 621–634.CrossRefGoogle Scholar
Kerswell, R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.CrossRefGoogle Scholar
King, B., Zhang, H. P. & Swinney, H. L. 2009 Tidal flows over three-dimensional topography in a stratified fluid. Phys. Fluids 21, 116601.CrossRefGoogle Scholar
Kistovich, Y. V. & Chashechkin, Y. D. 1994 Reflection of packets of internal waves from a rigid plane in a viscous fluid. Iz. Atmos. Ocean. Phys. 30, 752–758.Google Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45, 035504.CrossRefGoogle Scholar
Lamb, K. G. 2004 Nonlinear interaction among internal wave beams generated by tidal flow over supercritical topography. Geophys. Res. Lett. 31, 09313.CrossRefGoogle Scholar
Le Bars, M., Cébron, D. & Le Gal, P. 2015 Flows driven by libration, precession, and tides. Annu. Rev. Fluid Mech. 47, 163–193.CrossRefGoogle Scholar
Le Dizès, S. 2015 Wave field and zonal flow of a librating disk. J. Fluid Mech. 782, 178–208.CrossRefGoogle Scholar
Le Dizès, S. & Le Bars, M. 2017 Internal shear layers from librating objects. J. Fluid Mech. 826, 653–675.CrossRefGoogle Scholar
Lin, Y. & Noir, J. 2020 Libration-driven inertial waves and mean zonal flows in spherical shells. Geophys. Astrophys. Fluid Dyn. (accepted).CrossRefGoogle Scholar
Llewellyn Smith, S. G. & Young, W. R. 2003 Tidal conversion at a very steep ridge. J. Fluid Mech. 495, 175–191.CrossRefGoogle Scholar
Maas, L. R. M., Benielli, D., Sommeria, J. & Lam, F.-P. A. 1997 Observation of an internal wave attractor in a confined, stably stratified fluid. Nature 388, 557–561.CrossRefGoogle Scholar
Machicoane, N., Cortet, P.-P., Voisin, B. & Moisy, F. 2015 Influence of the multipole order of the source on the decay of an inertial wave beam in a rotating fluid. Phys. Fluids 27, 066602.CrossRefGoogle Scholar
McEwan, A. D. & Plumb, R. A. 1977 Off-resonant amplification of finite internal wave packets. Dyn. Atmos. Oceans 2, 83–105.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Phil. Trans. R. Soc. A 264, 597–634.Google Scholar
Morize, C., Le Bars, M., Le Gal, P. & Tilgner, A. 2010 Experimental determination of zonal winds driven by tides. Phys. Rev. Lett. 104, 214501.CrossRefGoogle ScholarPubMed
Noir, J., Jault, D. & Cardin, P. 2001 Numerical study of the motions within a slowly precessing sphere at low Ekman number. J. Fluid Mech. 437, 283–299.CrossRefGoogle Scholar
Peacock, T. & Tabaei, A. 2005 Visualization of nonlinear effects in reflecting internal wave beams. Phys. Fluids 17, 061702.CrossRefGoogle Scholar
Peat, K. S. 1978 Internal and inertial waves in a viscous rotating stratified fluid. Appl. Sci. Res. 33, 481–499.CrossRefGoogle Scholar
Phillips, O. M. 1966 The Dynamics of the Upper Ocean. Cambridge University Press.Google Scholar
Proudman, I. 1956 The almost-rigid rotation of viscous fluid between concentric spheres. J. Fluid Mech. 1, 505–516.CrossRefGoogle Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.CrossRefGoogle Scholar
Rieutord, M. & Valdettaro, L. 2010 Viscous dissipation by tidally forced inertial modes in a rotating spherical shell. J. Fluid Mech. 643, 363–394.CrossRefGoogle Scholar
Rodenborn, B., Kiefer, D., Zhang, H. P. & Swinney, H. L. 2011 Harmonic generation by reflecting internal waves. Phys. Fluids 23, 026601.CrossRefGoogle Scholar
Sauret, A., Cébron, D., Morize, C. & Le Bars, M. 2010 Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662, 260–268.CrossRefGoogle Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.CrossRefGoogle Scholar
St Laurent, L., Stringer, S., Garrett, C. & Perrault-Joncas, D. 2003 The generation of internal tides at abrupt topography. Deep-Sea Res. I 50, 987–1003.CrossRefGoogle Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34, 559–593.CrossRefGoogle Scholar
Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26, 131–144.CrossRefGoogle Scholar
Tabaei, A. & Akylas, T. R. 2003 Nonlinear internal gravity wave beams. J. Fluid Mech. 482, 141–161.CrossRefGoogle Scholar
Tabaei, A., Akylas, T. R. & Lamb, K. G. 2005 Nonlinear effects in reflecting and colliding internal wave beams. J. Fluid Mech. 526, 217–243.CrossRefGoogle Scholar
Thomas, N. H. & Stevenson, T. N. 1972 A similarity solution for viscous internal waves. J. Fluid Mech. 54, 495–506.CrossRefGoogle Scholar
Tilgner, A. 2000 Oscillatory shear layers in source driven flows in an unbounded rotating fluid. Phys. Fluids 12, 1101–11.CrossRefGoogle Scholar
Tilgner, A. 2007 Zonal wind driven by inertial modes. Phys. Rev. Lett. 99, 194501.CrossRefGoogle ScholarPubMed
Voisin, B. 2003 Limit states of internal wave beams. J. Fluid Mech. 496, 243–293.CrossRefGoogle Scholar
Walton, I. C. 1975 Viscous shear layers in an oscillating rotating fluid. Proc. R. Soc. Lond. A 344, 101–110.Google Scholar
Wunsch, C. 1975 Internal tides in the ocean. Rev. Geophys. Space Phys. 13, 167–182.CrossRefGoogle Scholar
Zhang, H. P., King, B. & Swinney, H. L. 2007 Experimental study of internal gravity waves generated by supercritical topography. Phys. Fluids 19, 096602.CrossRefGoogle Scholar