Published online by Cambridge University Press: 09 October 2020
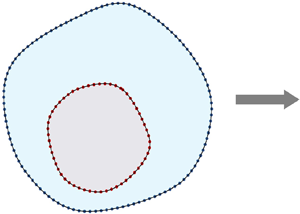
This study presents a class of steadily translating two-dimensional approximately circular vortices. The proposed solutions take the form of a superposition of two nearly concentric vorticity patches with zero net vorticity. Exact quasi-monopolar solutions of this type are found for propagation speeds that are much less than typical azimuthal velocities. While all V-states obtained are shown to be formally unstable, a large subset of configurations is characterized by very low growth rates. Fully nonlinear simulations reveal that such nearly stable eddies can propagate large distances from the point of origin while maintaining their structure and intensity. Therefore, the proposed solutions can serve as models of geophysical vortices that are known to drift relative to the ambient fluid, often exhibiting remarkable longevity and resilience to external perturbations.