Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T01:11:36.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Prediction of shear thickening of particle suspensions in viscoelastic fluids by direct numerical simulation

Published online by Cambridge University Press:  01 March 2021

Yuki Matsuoka Open the ORCID record for Yuki Matsuoka [Opens in a new window] ,
Yasuya Nakayama  and
Toshihisa Kajiwara
Yuki Matsuoka*
Affiliation:
Corporate Engineering Center, Sumitomo Bakelite Co. Ltd, Shizuoka426-0041, Japan Department of Chemical Engineering, Kyushu University, Fukuoka819-0395, Japan
Yasuya Nakayama*
Affiliation:
Department of Chemical Engineering, Kyushu University, Fukuoka819-0395, Japan
Toshihisa Kajiwara
Affiliation:
Department of Chemical Engineering, Kyushu University, Fukuoka819-0395, Japan
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

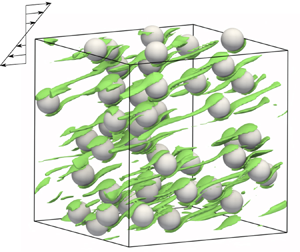
To elucidate the key factor for the quantitative prediction of the shear thickening in suspensions in viscoelastic fluids, direct numerical simulations of many-particle suspensions in a multi-mode Oldroyd-B fluid are performed using the smoothed profile method. Suspension flow under simple shear flow is solved under periodic boundary conditions by using Lees–Edwards boundary conditions for particle dynamics and a time-dependent oblique coordinate system that evolves with mean shear flow for fluid dynamics. Semidilute many-particle suspensions up to a particle volume fraction of 0.1 are investigated. The presented numerical results regarding the bulk rheological properties of the shear-thickening behaviour agree quantitatively with recent experimental results of semidilute suspensions in a Boger fluid. The presented result clarifies that an accurate estimation of the first normal stress difference of the matrix in the shear-rate range where the shear thickening starts to occur is crucial for the quantitative prediction of the suspension shear thickening in a Boger fluid matrix at around the Weissenberg number ${Wi}=1$ by an Oldroyd-B model. Additionally, the effect of suspension microstructures on the suspension viscosity is examined. The paper concludes with a discussion on how the flow pattern and the elastic stress development change with the volume fraction and Weissenberg number.

JFM classification

Complex Fluids: Suspensions Non-Newtonian Flows: Rheology Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A38
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alghalibi, D., Lashgari, I., Brandt, L. & Hormozi, S. 2018 Interface-resolved simulations of particle suspensions in Newtonian, shear thinning and shear thickening carrier fluids. J. Fluid Mech. 852, 329–357.CrossRefGoogle Scholar
Batchelor, G.K. & Green, J.T. 1972 The determination of the bulk stress in a suspension of spherical particles to order c2. J. Fluid Mech. 56 (3), 401–427.CrossRefGoogle Scholar
Beylkin, G., Keiser, J.M. & Vozovoi, L. 1998 A new class of time discretization schemes for the solution of nonlinear PDEs. J. Comput. Phys. 147 (2), 362–387.CrossRefGoogle Scholar
Bird, R.B., Curtiss, C.F., Armstrong, R.C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory. Wiley.Google Scholar
Boger, D.V. 1977 A highly elastic constant-viscosity fluid. J. Non-Newtonian Fluid Mech. 3 (1), 87–91.CrossRefGoogle Scholar
Canuto, C., Hussaini, M.Y., Quarteroni, A. & Zang, T.A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Chateau, X., Ovarlez, G. & Trung, K.L. 2008 Homogenization approach to the behavior of suspensions of noncolloidal particles in yield stress fluids. J. Rheol. 52 (2), 489–506.CrossRefGoogle Scholar
Dai, S.-C., Qi, F. & Tanner, R.I. 2014 Viscometric functions of concentrated non-colloidal suspensions of spheres in a viscoelastic matrix. J. Rheol. 58 (1), 183–198.CrossRefGoogle Scholar
D'Avino, G., Greco, F., Hulsen, M.A. & Maffettone, P.L. 2013 Rheology of viscoelastic suspensions of spheres under small and large amplitude oscillatory shear by numerical simulations. J. Rheol. 57 (3), 813–839.CrossRefGoogle Scholar
D'Avino, G., Hulsen, M.A., Snijkers, F., Vermant, J., Greco, F. & Maffettone, P.L. 2008 Rotation of a sphere in a viscoelastic liquid subjected to shear flow. Part I: simulation results. J. Rheol. 52 (6), 1331–1346.CrossRefGoogle Scholar
Einarsson, J., Yang, M. & Shaqfeh, E.S.G. 2018 Einstein viscosity with fluid elasticity. Phys. Rev. Fluids 3 (1), 013301.CrossRefGoogle Scholar
Einstein, A. 1911 Berichtigung zu meiner Arbeit: Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 339, 591–592.CrossRefGoogle Scholar
Fattal, R. & Kupferman, R. 2004 Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newtonian Fluid Mech. 123 (2–3), 281–285.CrossRefGoogle Scholar
Fernandes, C., Faroughi, S.A., Carneiro, O.S., Nóbrega, J.M. & McKinley, G.H. 2019 Fully-resolved simulations of particle-laden viscoelastic fluids using an immersed boundary method. J. Non-Newtonian Fluid Mech. 266 (February), 80–94.CrossRefGoogle Scholar
Haddadi, H. & Morris, J.F. 2014 Microstructure and rheology of finite inertia neutrally buoyant suspensions. J. Fluid Mech. 749 (3), 431–459.CrossRefGoogle Scholar
Housiadas, K.D. & Tanner, R.I. 2011 a Perturbation solution for the viscoelastic 3D flow around a rigid sphere subject to simple shear. Phys. Fluids 23 (8), 083101.CrossRefGoogle Scholar
Housiadas, K.D. & Tanner, R.I. 2011 b The angular velocity of a freely rotating sphere in a weakly viscoelastic matrix fluid. Phys. Fluids 23 (5), 051702.CrossRefGoogle Scholar
Housiadas, K.D. & Tanner, R.I. 2018 Viscoelastic shear flow past an infinitely long and freely rotating cylinder. Phys. Fluids 30 (7), 073101.CrossRefGoogle Scholar
Hulsen, M.A., Fattal, R. & Kupferman, R. 2005 Flow of viscoelastic fluids past a cylinder at high Weissenberg number: stabilized simulations using matrix logarithms. J. Non-Newtonian Fluid Mech. 127 (1), 27–39.CrossRefGoogle Scholar
Hwang, W.R. & Hulsen, M.A. 2011 Structure formation of non-colloidal particles in viscoelastic fluids subjected to simple shear flow. Macromol. Mater. Engng 296 (3–4), 321–330.CrossRefGoogle Scholar
Hwang, W.R., Hulsen, M.A. & Meijer, H.E.H. 2004 Direct simulations of particle suspensions in a viscoelastic fluid in sliding bi-periodic frames. J. Non-Newtonian Fluid Mech. 121 (1), 15–33.CrossRefGoogle Scholar
Iwashita, T., Kumagai, T. & Yamamoto, R. 2010 A direct numerical simulation method for complex modulus of particle dispersions. Eur. Phys. J. E 32 (4), 357–363.CrossRefGoogle ScholarPubMed
Iwashita, T. & Yamamoto, R. 2009 Direct numerical simulations for non-Newtonian rheology of concentrated particle dispersions. Phys. Rev. E 80 (6), 061402.CrossRefGoogle ScholarPubMed
Jaensson, N.O., Hulsen, M.A. & Anderson, P.D. 2015 Simulations of the start-up of shear flow of 2D particle suspensions in viscoelastic fluids: structure formation and rheology. J. Non-Newtonian Fluid Mech. 225, 70–85.CrossRefGoogle Scholar
Jaensson, N.O., Hulsen, M.A. & Anderson, P.D. 2016 Direct numerical simulation of particle alignment in viscoelastic fluids. J. Non-Newtonian Fluid Mech. 235, 125–142.CrossRefGoogle Scholar
James, D.F. 2009 Boger Fluids. Annu. Rev. Fluid Mech. 41 (1), 129–142.CrossRefGoogle Scholar
Ji, S., Jiang, R., Winkler, R.G. & Gompper, G. 2011 Mesoscale hydrodynamic modeling of a colloid in shear-thinning viscoelastic fluids under shear flow. J. Chem. Phys. 135 (13), 134116.CrossRefGoogle ScholarPubMed
Kim, K., Nakayama, Y. & Yamamoto, R. 2006 Direct numerical simulations of electrophoresis of charged colloids. Phys. Rev. Lett. 96 (20), 208302.CrossRefGoogle ScholarPubMed
Kobayashi, H. & Yamamoto, R. 2011 Implementation of Lees-Edwards periodic boundary conditions for direct numerical simulations of particle dispersions under shear flow. J. Chem. Phys. 134 (6), 064110.CrossRefGoogle ScholarPubMed
Koch, D.L., Lee, E.F. & Mustafa, I. 2016 Stress in a dilute suspension of spheres in a dilute polymer solution subject to simple shear flow at finite Deborah numbers. Phys. Rev. Fluids 1 (1), 013301.CrossRefGoogle Scholar
Lees, A.W. & Edwards, S.F. 1972 The computer study of transport processes under extreme conditions. J. Phys. C 5 (15), 1921–1928.CrossRefGoogle Scholar
Lin, Ch.J., Peery, J.H. & Schowalter, W.R. 1970 Simple shear flow round a rigid sphere: inertial effects and suspension rheology. J. Fluid Mech. 44 (1), 1–17.CrossRefGoogle Scholar
Luo, H. & Bewley, T.R. 2004 On the contravariant form of the Navier–Stokes equations in time-dependent curvilinear coordinate systems. J. Comput. Phys. 199 (1), 355–375.CrossRefGoogle Scholar
Luo, X., Beskok, A. & Karniadakis, G.E. 2010 Modeling electrokinetic flows by the smoothed profile method. J. Comput. Phys. 229 (10), 3828–3847.CrossRefGoogle ScholarPubMed
Matsuoka, Y., Fukasawa, T., Higashitani, K. & Yamamoto, R. 2012 Effect of hydrodynamic interactions on rapid Brownian coagulation of colloidal dispersions. Phys. Rev. E 86 (5), 051403.CrossRefGoogle ScholarPubMed
Matsuoka, Y., Nakayama, Y. & Kajiwara, T. 2020 Effects of viscoelasticity on shear-thickening in dilute suspensions in a viscoelastic fluid. Soft Matt. 16 (3), 728–737.CrossRefGoogle Scholar
Michele, J., Pätzold, R. & Donis, R. 1977 Alignment and aggregation effects in suspensions of spheres in non-Newtonian media. Rheol. Acta 16 (3), 317–321.CrossRefGoogle Scholar
Mikulencak, D.R. & Morris, J.F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215–242.CrossRefGoogle Scholar
Molina, J.J., Nakayama, Y. & Yamamoto, R. 2013 Hydrodynamic interactions of self-propelled swimmers. Soft Matt. 9 (19), 4923–4936.CrossRefGoogle Scholar
Molina, J.J., Otomura, K., Shiba, H., Kobayashi, H., Sano, M. & Yamamoto, R. 2016 Rheological evaluation of colloidal dispersions using the smoothed profile method: formulation and applications. J. Fluid Mech. 792, 590–619.CrossRefGoogle Scholar
Nakayama, Y., Kajiwara, T. & Masaki, T. 2016 Strain mode of general flow: characterization and implications for flow pattern structures. AIChE J. 62 (7), 2563–2569.CrossRefGoogle Scholar
Nakayama, Y., Kim, K. & Yamamoto, R. 2008 Simulating (electro)hydrodynamic effects in colloidal dispersions: smoothed profile method. Eur. Phys. J. E 26 (4), 361–368.CrossRefGoogle ScholarPubMed
Nakayama, Y. & Yamamoto, R. 2005 Simulation method to resolve hydrodynamic interactions in colloidal dispersions. Phys. Rev. E 71 (3), 036707.CrossRefGoogle ScholarPubMed
Nunan, K.C. & Keller, J.B. 1984 Effective viscosity of a periodic suspension. J. Fluid Mech. 142, 269–287.CrossRefGoogle Scholar
Onuki, A. 1997 A new computer method of solving dynamic equations under externally applied deformations. J. Phys. Soc. Japan 66 (6), 1836–1837.CrossRefGoogle Scholar
Orszag, S.A. 1969 Numerical methods for the simulation of turbulence. Phys. Fluids 12 (12), II-250.CrossRefGoogle Scholar
Phan-Thien, N., Tran-Cong, T. & Graham, A.L. 1991 Shear flow of periodic arrays of particle clusters: a boundary-element method. J. Fluid Mech. 228 (1991), 275–293.Google Scholar
Rogallo, R.S. 1981 Numerical experiments in homogeneous turbulence. NASA Tech. Memo. 81315.Google Scholar
Scirocco, R., Vermant, J. & Mewis, J. 2004 Effect of the viscoelasticity of the suspending fluid on structure formation in suspensions. J. Non-Newtonian Fluid Mech. 117 (2–3), 183–192.CrossRefGoogle Scholar
Scirocco, R., Vermant, J. & Mewis, J. 2005 Shear thickening in filled Boger fluids. J. Rheol. 49 (2), 551–567.CrossRefGoogle Scholar
Shaqfeh, E.S.G. 2019 On the rheology of particle suspensions in viscoelastic fluids. AIChE J. 65 (5), e16575.CrossRefGoogle Scholar
Snijkers, F., D'Avino, G., Maffettone, P.L., Greco, F., Hulsen, M.A. & Vermant, J. 2009 Rotation of a sphere in a viscoelastic liquid subjected to shear flow. Part II. Experimental results. J. Rheol. 53 (2), 459–480.CrossRefGoogle Scholar
Snijkers, F., D'Avino, G., Maffettone, P.L., Greco, F., Hulsen, M.A. & Vermant, J. 2011 Effect of viscoelasticity on the rotation of a sphere in shear flow. J. Non-Newtonian Fluid Mech. 166 (7–8), 363–372.CrossRefGoogle Scholar
Tanner, R.I. 2015 Non-colloidal suspensions: relations between theory and experiment in shearing flows. J. Non-Newtonian Fluid Mech. 222, 18–23.CrossRefGoogle Scholar
Tanner, R.I. 2019 Review: rheology of noncolloidal suspensions with non-Newtonian matrices. J. Rheol. 63 (4), 705–717.CrossRefGoogle Scholar
Vázquez-Quesada, A. & Ellero, M. 2017 SPH modeling and simulation of spherical particles interacting in a viscoelastic matrix. Phys. Fluids 29 (12), 121609.CrossRefGoogle Scholar
Vázquez-Quesada, A., Espa nol, P., Tanner, R.I. & Ellero, M. 2019 Shear thickening of a non-colloidal suspension with a viscoelastic matrix. J. Fluid Mech. 880, 1070–1094.CrossRefGoogle Scholar
Venturi, D. 2009 Convective derivatives and Reynolds transport in curvilinear time-dependent coordinates. J. Phys. A 42 (12), 125203.CrossRefGoogle Scholar
Yang, M., Krishnan, S. & Shaqfeh, E.S.G. 2016 Numerical simulations of the rheology of suspensions of rigid spheres at low volume fraction in a viscoelastic fluid under shear. J. Non-Newtonian Fluid Mech. 233, 181–197.CrossRefGoogle Scholar
Yang, M. & Shaqfeh, E.S.G. 2018 a Mechanism of shear thickening in suspensions of rigid spheres in Boger fluids. Part I: dilute suspensions. J. Rheol. 62 (6), 1363–1377.CrossRefGoogle Scholar
Yang, M. & Shaqfeh, E.S.G. 2018 b Mechanism of shear thickening in suspensions of rigid spheres in Boger fluids. Part II: suspensions at finite concentration. J. Rheol. 62 (6), 1379–1396.CrossRefGoogle Scholar
Zarraga, I.E., Hill, D.A. & Leighton, D.T. 2001 Normal stresses and free surface deformation in concentrated suspensions of noncolloidal spheres in a viscoelastic fluid. J. Rheol. 45 (5), 1065–1084.CrossRefGoogle Scholar