Published online by Cambridge University Press: 22 November 2018
Researches on nonlinear instability of power-law plane sheets have been conducted using the Carreau model as the constitutive model. Combined with asymptotic expansion and long-wave assumption, the governing equations and boundary conditions were manipulated using integral transform. The first-order dimensionless dispersion relation between unstable growth rate and wavenumber was obtained and the second-order interface disturbance amplitude was calculated. By comparison and analysis of components of the second-order interface disturbance amplitude, it was found that the power-law index  $n$ (
$n$ (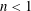 $n<1$) only had an impact on instability of waves with the fundamental wavelength or one third the fundamental wavelength. The findings show that the Carreau-law rheological parameter
$n<1$) only had an impact on instability of waves with the fundamental wavelength or one third the fundamental wavelength. The findings show that the Carreau-law rheological parameter 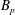 $B_{p}$ has little impact on the second-order disturbance amplitude at the interfaces in a practical situation, while the Reynolds number has a positive effect on the growth rate of the disturbance amplitude for the power-law liquid sheets. Finally, the growth rates obtained by numerical simulation and analytical solution have been compared, and the results showed good agreement in the initial phase of wave evolution.
$B_{p}$ has little impact on the second-order disturbance amplitude at the interfaces in a practical situation, while the Reynolds number has a positive effect on the growth rate of the disturbance amplitude for the power-law liquid sheets. Finally, the growth rates obtained by numerical simulation and analytical solution have been compared, and the results showed good agreement in the initial phase of wave evolution.