Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:52:47.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed baroclinic convection in a cavity

Published online by Cambridge University Press:  07 January 2020

Abhishek Kumar Open the ORCID record for Abhishek Kumar [Opens in a new window]  and
Alban Pothérat Open the ORCID record for Alban Pothérat [Opens in a new window]
Abhishek Kumar*
Affiliation:
Centre for Fluid and Complex Systems, Coventry University, CoventryCV1 5FB, UK
Alban Pothérat
Affiliation:
Centre for Fluid and Complex Systems, Coventry University, CoventryCV1 5FB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

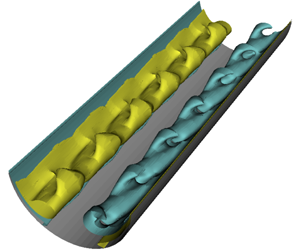
We study the convective patterns that arise in a nearly semicylindrical cavity fed in with hot fluid at the upper boundary, bounded by a cold, porous semicircular boundary at the bottom, and infinitely extended in the third direction. While this configuration is relevant to continuous casting processes that are significantly more complex, we focus on the flow patterns associated with the particular form of mixed convection that arises in it. Linear stability analysis (LSA) and direct numerical simulations (DNS) are conducted, using the spectral-element method to identify observable states. The nature of the bifurcations is determined through Stuart–Landau analysis for completeness. The base flow consists of two counter-rotating rolls driven by the baroclinic imbalance due to the curved isothermal boundary. These are, however, suppressed by the through-flow, which is found to have a stabilising influence as soon as the Reynolds number $Re$ based on the through-flow exceeds 25. For a sufficiently high Rayleigh number, this base flow is linearly unstable to three different modes, depending on $Re$. For $Re\leqslant 75$, the rolls destabilise through a supercritical bifurcation into a travelling wave. For $100\leqslant Re\leqslant 110$, a subcritical bifurcation leads to a standing oscillatory mode, whereas for $Re\geqslant 150$, the unstable mode is non-oscillatory and grows out of a supercritical bifurcation. The DNS confirm that in all cases the dominant mode returned by the LSA precisely matches the topology and evolution of the flow patterns that arise out of the fully nonlinear dynamics.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Convection: Buoyancy-driven instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A40
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albarède, P. & Provansal, M. 1995 Quasi-periodic cylinder wakes and the Ginzburg–Landau model. J. Fluid Mech. 291, 191–222.CrossRefGoogle Scholar
Aujogue, K., Pothérat, A. & Sreenivasan, B. 2015 Onset of plane layer magnetoconvection at low Ekman number. Phys. Fluids 27 (10), 106602.CrossRefGoogle Scholar
Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57 (9), 1435–1458.CrossRefGoogle Scholar
Barkley, D., Gomes, M. G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Briggs, D. G. & Jones, D. N. 1985 Two-dimensional periodic natural convection in a rectangular enclosure of aspect ratio one. Trans. ASME J. Heat Transfer 107 (4), 850–854.CrossRefGoogle Scholar
Cantwell, C. D., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., Grazia, D. D., Yakovlev, S., Lombard, J. E., Ekelschot, D. et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zhang, T. A. 1988 Spectral Methods in Fluid Turbulence. Springer.CrossRefGoogle Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.CrossRefGoogle Scholar
Chandrasekhar, S. 1968 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Clever, R. M. & Busse, F. H. 1974 Transition to time-dependent convection. J. Fluid Mech. 65 (4), 625–645.CrossRefGoogle Scholar
Clune, T. & Knobloch, E. 1993 Pattern selection in rotating convection with experimental boundary conditions. Phys. Rev. E 47 (4), 2536–2540.Google ScholarPubMed
Dorward, R. C., Beerntsen, D. J. & Brwon, K. R. 1996 Banded segregation patterns in DC-cast Al–Zn–Mg–Cu alloy ingots and their effect on plate properties. Aluminium 72 (4), 251–259.Google Scholar
Dušek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
Flood, S. C. & Davidson, P. A. 1994 Natural convection in aluminium direct chill cast ingot. Mater. Sci. Technol. 10 (8), 741–752.CrossRefGoogle Scholar
Fujimura, K. & Kelly, R. E. 1993 Mixed mode convection in an inclined slot. J. Fluid Mech. 246, 545–568.CrossRefGoogle Scholar
Fujimura, K. & Kelly, R. E. 1995 Interaction between longitudinal convection rolls and transverse waves in unstably stratified plane Poiseuille flow. Phys. Fluids 7 (1), 68–79.CrossRefGoogle Scholar
Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33 (1), 21–32.CrossRefGoogle Scholar
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh reference manual. Gmsh: a three-dimensional finite element mesh generator with built-in pre-and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.CrossRefGoogle Scholar
Guervilly, C. & Cardin, P. 2016 Subcritical convection of liquid metals in a rotating sphere using a quasi-geostrophic model. J. Fluid Mech. 808, 61–89.CrossRefGoogle Scholar
Hart, J. E. 1971 Stability of the flow in a differentially heated inclined box. J. Fluid Mech. 47 (3), 547–576.CrossRefGoogle Scholar
Hart, J. E. 1979 Finite amplitude baroclinic instability. Annu. Rev. Fluid Mech. 11 (1), 147–172.CrossRefGoogle Scholar
Henderson, R. D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8 (6), 1683–1685.CrossRefGoogle Scholar
Jaluria, Y. 1980 Natural Convection Heat and Mass Transfer. Pergamon.Google Scholar
James, I. N. 1987 Suppression of baroclinic instability in horizontally sheared flows. J. Atmos. Sci. 44 (24), 3710–3720.2.0.CO;2>CrossRefGoogle Scholar
Karniadakis, G. & Sherwin, S. J. 1999 Spectral/hp Element Methods for CFD. Oxford University Press.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Kelly, R. E. 1994 The onset and development of thermal convection in fully developed shear flows. Adv. Appl. Mech. 31, 35–112.CrossRefGoogle Scholar
Korpela, S. A. 1974 A study on the effect of Prandtl number on the stability of the conduction regime of natural convection in an inclined slot. Intl J. Heat Mass Transfer 17 (2), 215–222.CrossRefGoogle Scholar
Kuznetsov, A. V. 1997 Double-diffusive convection during continuous strip casting. In CHT’97 – Advances in Computational Heat Transfer, Proceedings of the International Symposium – Çesme, Turkey, May 26–30, 1997. Begell House.Google Scholar
Landau, L. D. 1944 On the problem of turbulence. C. R. Acad. Sci. UESS 44, 311.Google Scholar
Landau, L. D. & Lifsitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
Mao, X. & Blackburn, H. M. 2014 The structure of primary instability modes in the steady wake and separation bubble of a square cylinder. Phys. Fluids 26 (7), 074103.CrossRefGoogle Scholar
Nakagawa, Y. 1957 Experiments on the instability of a layer of mercury heated from below and subject to the simultaneous action of a magnetic field and rotation. Proc. R. Soc. Lond. A 242 (1228), 81–88.Google Scholar
Nicolas, X., Luijkx, J.-M. & Platten, J.-K. 2000 Linear stability of mixed convection flows in horizontal rectangular channels of finite transversal extension heated from below. Intl J. Heat Mass Transfer 43 (4), 589–610.CrossRefGoogle Scholar
Papanicolaou, E. & Jaluria, Y. 1992 Transition to a periodic regime in mixed convection in a square cavity. J. Fluid Mech. 239, 489–509.CrossRefGoogle Scholar
Pierrehumbert, R. T. & Swanson, K. L. 1995 Baroclinic instability. Annu. Rev. Fluid Mech. 27 (1), 419–467.CrossRefGoogle Scholar
Pitz, D. B., Marxen, O. & Chew, J. W. 2017 Onset of convection induced by centrifugal buoyancy in a rotating cavity. J. Fluid Mech. 826, 484–502.CrossRefGoogle Scholar
Pothérat, A. & Zhang, L.2018 Dean flow and vortex shedding in a three-dimensional $180^{\circ }$ sharp bend. arXiv:1807.10950.Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Sapardi, A. M., Hussam, W. K., Pothérat, A. & Sheard, G. J. 2017 Linear stability of confined flow around a 180° sharp bend. J. Fluid Mech. 822, 813–847.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Schumm, M., Berger, E. & Monkewitz, P. A. 1994 Self-excited oscillations in the wake of two-dimensional bluff bodies and their control. J. Fluid Mech. 271, 17–53.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.CrossRefGoogle Scholar
Sheng, D. Y. & Jonsson, L. 2000 Two-fluid simulation on the mixed convection flow pattern in a nonisothermal water model of continuous casting tundish. Metall. Mater. Trans. B 31 (4), 867–875.CrossRefGoogle Scholar
Shome, B. & Jensen, M. K. 1995 Mixed convection laminar flow and heat transfer of liquids in isothermal horizontal circular ducts. Intl J. Heat Mass Transfer 38 (11), 1945–1956.CrossRefGoogle Scholar
Stuart, J. T. 1958 On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 4 (1), 1–21.CrossRefGoogle Scholar
Stuart, J. T. 1960 On the non-linear mechanics of disturbances in parallel flows, Part 1. The basic behavior in plane Poiseuille flow. J. Fluid Mech. 9, 353–370.CrossRefGoogle Scholar
Thomas, B. G. & Zhang, L. 2001 Mathematical modeling of fluid flow in continuous casting. ISIJ International 41 (10), 1181–1193.CrossRefGoogle Scholar
Thomas, L., Pesch, W. & Ahlers, G. 1998 Rayleigh–Bénard convection in a homeotropically aligned nematic liquid crystal. Phys. Rev. E 58 (5), 5885–5897.Google Scholar
Thompson, M. C. & Le Gal, P. 2004 The Stuart–Landau model applied to wake transition revisited. Eur. J. Mech. (B/Fluids) 23 (1), 219–228.CrossRefGoogle Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics. Clarendon.Google Scholar
Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for timesteppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems, pp. 453–466. Springer.CrossRefGoogle Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J. et al. 2019 SciPy 1.0–fundamental algorithms for scientific computing in Python. arXiv:1907.10121.Google Scholar
Vo, T., Pothérat, A. & Sheard, G. J. 2017 Linear stability of horizontal, laminar fully developed, quasi-two-dimensional liquid metal duct flow under a transverse magnetic field and heated from below. Phys. Rev. Fluids 2 (3), 033902.CrossRefGoogle Scholar
Vos, P. E. J., Eskilsson, C., Bolis, A., Chun, S., Kirby, R. M. & Sherwin, S. J. 2011 A generic framework for time-stepping partial differential equations (PDEs): general linear methods, object-oriented implementation and application to fluid problems. Intl J. Comput. Fluid Dyn. 25 (3), 107–125.CrossRefGoogle Scholar

Kumar and Pothérat supplementary movie 1

A movie representing the travelling wave at $Re=0$ and $Ra=7 imes 10^3$ for $\zeta_z$. The color-coding of the movie corresponds to figure 12(d).
Download Kumar and Pothérat supplementary movie 1(Video)
Video 11.6 MB

Kumar and Pothérat supplementary movie 2

A movie representing the standing wave at $Re=100$ and $Ra=4 imes 10^4$ for $\zeta_z$.The color-coding of the movie corresponds to figure 13(d).
Download Kumar and Pothérat supplementary movie 2(Video)
Video 9.8 MB