Published online by Cambridge University Press: 05 December 2013
The generation of distinct polygonal configurations via the instability of a Stewartson shear layer is numerically investigated. The shear layer is induced using a rotating cylindrical tank with differentially forced disks located at the top and bottom boundaries. The incompressible Navier–Stokes equations are solved on a two-dimensional semi-meridional plane. Axisymmetric base flows are consistently found to reach a steady state for a wide range of flow conditions, and details of the vertical structure are revealed. An axially invariant two-dimensional flow is ascertained for small 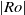 $\vert \mathit{Ro}\vert $, which substantiates the Taylor–Proudman theorem. Sufficient increases in
$\vert \mathit{Ro}\vert $, which substantiates the Taylor–Proudman theorem. Sufficient increases in 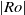 $\vert \mathit{Ro}\vert $ forcing develops flow features that break this quasi-two-dimensionality. The onset of this breaking occurs earlier with increasing
$\vert \mathit{Ro}\vert $ forcing develops flow features that break this quasi-two-dimensionality. The onset of this breaking occurs earlier with increasing 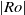 $\vert \mathit{Ro}\vert $ for
$\vert \mathit{Ro}\vert $ for 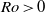 $\mathit{Ro}\gt 0$ compared with
$\mathit{Ro}\gt 0$ compared with 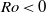 $\mathit{Ro}\lt 0$. The thickness scaling of the vertical Stewartson layers are in agreement with previous analytical results. Growth rates of the most unstable azimuthal wavenumber from a global linear stability analysis are obtained. The threshold between axisymmetric and non-axisymmetric flow follows a power law, and both positive- and negative-
$\mathit{Ro}\lt 0$. The thickness scaling of the vertical Stewartson layers are in agreement with previous analytical results. Growth rates of the most unstable azimuthal wavenumber from a global linear stability analysis are obtained. The threshold between axisymmetric and non-axisymmetric flow follows a power law, and both positive- and negative-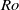 $\mathit{Ro}$ regimes are found to adopt the same threshold for instability, namely
$\mathit{Ro}$ regimes are found to adopt the same threshold for instability, namely 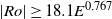 $\vert \mathit{Ro}\vert \geq 18. 1{E}^{0. 767} $. This relationship corresponds to a constant critical internal Reynolds number of
$\vert \mathit{Ro}\vert \geq 18. 1{E}^{0. 767} $. This relationship corresponds to a constant critical internal Reynolds number of 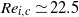 ${\mathit{Re}}_{i, c} \simeq 22. 5$. A review of reported critical internal Reynolds number and their characteristic length scales yields a consistent instability onset given by
${\mathit{Re}}_{i, c} \simeq 22. 5$. A review of reported critical internal Reynolds number and their characteristic length scales yields a consistent instability onset given by 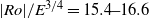 $\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 4{\unicode{x2013}} 16. 6$; here we find
$\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 4{\unicode{x2013}} 16. 6$; here we find 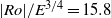 $\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 8$. At the onset of linear instability, the initially circular shear layer deforms, resulting in a polygonal structure consistent with barotropic instability. Dominant azimuthal wavenumbers range from
$\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 8$. At the onset of linear instability, the initially circular shear layer deforms, resulting in a polygonal structure consistent with barotropic instability. Dominant azimuthal wavenumbers range from 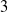 $3$ to
$3$ to 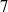 $7$ at the onset of instability for the parameter space explored. Empirical relationships for the preferential wavenumber have been obtained. Additional instability modes have been discovered that favour higher wavenumbers, and these exhibit structures localized to the disk–tank interfaces.
$7$ at the onset of instability for the parameter space explored. Empirical relationships for the preferential wavenumber have been obtained. Additional instability modes have been discovered that favour higher wavenumbers, and these exhibit structures localized to the disk–tank interfaces.
Present address: Space Science Institute, Boulder, CO 80301, USA.