Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T02:31:54.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability analysis for flows over sinusoidal bottom topography

Published online by Cambridge University Press:  28 January 2021

Jack Davies Open the ORCID record for Jack Davies [Opens in a new window] ,
Hemant Khatri Open the ORCID record for Hemant Khatri [Opens in a new window]  and
Pavel Berloff Open the ORCID record for Pavel Berloff [Opens in a new window]
Jack Davies*
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK
Hemant Khatri
Affiliation:
Program in Atmospheric and Oceanic Sciences, Princeton University, Princeton, NJ08540, USA
Pavel Berloff
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK Institute of Numerical Mathematics of the Russian Academy of Sciences, 119333Moscow, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

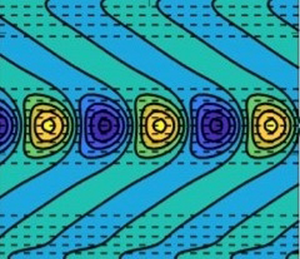
This is an ocean motivated study which investigates the impacts of sinusoidal bottom topography on baroclinic instability of zonal vertically sheared flows in the two-layer quasigeostrophic model. The corresponding linear stability problem is solved by assuming Fourier-mode solutions in both the zonal and meridional directions. In the presence of variable topographic features, the Fourier modes become coupled due to phase shifts in the wavevectors. The spectral discretisation method used in this work retains the primary relationship between different Fourier modes; thus, the linear stability eigenproblem can be solved for any periodic topography. Moreover, this method does not need any additional assumptions, such as considering small-amplitude or large-scale bottom irregularities, as in some previous studies. In this work, the eigenproblem is solved for a range of topographic amplitudes and wavenumbers, and their effects on the growth rates and shapes of the most unstable eigenmodes are discussed. In general, both the zonal and meridional variations in topography tend to suppress the baroclinic instability. However, it is found that only meridionally varying topography affects the magnitudes of the fastest growth rates. In this instance, unstable modes appear to form two clusters well separated in the zonal wavenumber axis and growth rate maxima occur at two distinct zonal wavenumbers. Dependencies of the characteristics of these clusters on the values of topography amplitude and ridge width are reviewed. Finally, doubly periodic numerical simulations are used to verify the results from the linear stability analysis.

JFM classification

Geophysical and Geological Flows: Topographic effects Geophysical and Geological Flows: Quasi-geostrophic flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A33
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abernathey, R. & Cessi, P. 2014 Topographic enhancement of eddy efficiency in baroclinic equilibration. J. Phys. Oceanogr. 44 (8), 2107–2126.CrossRefGoogle Scholar
Barthel, A., McC. Hogg, A., Waterman, S. & Keating, S. 2017 Jet–topography interactions affect energy pathways to the deep southern ocean. J. Phys. Oceanogr. 47 (7), 1799–1816.CrossRefGoogle Scholar
Benilov, E.S. 2000 a The stability of zonal jets in a rough-bottomed ocean on the barotropic beta plane. J. Phys. Oceanogr. 30 (4), 733–740.2.0.CO;2>CrossRefGoogle Scholar
Benilov, E.S. 2000 b Waves on the beta-plane over sparse topography. J. Fluid Mech. 423, 263–273.CrossRefGoogle Scholar
Benilov, E.S. 2001 Baroclinic instability of two-layer flows over one-dimensional bottom topography. J. Phys. Oceanogr. 31 (8), 2019–2025.2.0.CO;2>CrossRefGoogle Scholar
Benilov, E.S., Nycander, J. & Dritschel, D.G. 2004 Destabilization of barotropic flows small-scale topography. J. Fluid Mech. 517, 359–374.CrossRefGoogle Scholar
Berloff, P. & Kamenkovich, I. 2013 On spectral analysis of mesoscale eddies. Part 1. Linear analysis. J. Phys. Oceanogr. 43 (12), 2505–2527.CrossRefGoogle Scholar
Berloff, P., Kamenkovich, I. & Pedlosky, J. 2009 A mechanism of formation of multiple zonal jets in the oceans. J. Fluid Mech. 628, 395–425.CrossRefGoogle Scholar
Berloff, P., Karabasov, S., Farrar, J.T. & Kamenkovich, I. 2011 On latency of multiple zonal jets in the oceans. J. Fluid Mech. 686, 534–567.CrossRefGoogle Scholar
Boland, E., Thompson, A.F., Shuckburgh, E. & Haynes, P. 2012 The formation of nonzonal jets over sloped topography. J. Phys. Oceanogr. 42 (10), 1635–1651.CrossRefGoogle Scholar
Chapman, C.C., McC. Hogg, A., Kiss, A.E. & Rintoul, S.R. 2015 The dynamics of southern ocean storm tracks. J. Phys. Oceanogr. 45 (3), 884–903.CrossRefGoogle Scholar
Chelton, D.B., DeSzoeke, R.A., Schlax, M.G., El Naggar, K. & Siwertz, N. 1998 Geographical variability of the first baroclinic Rossby radius of deformation. J. Phys. Oceanogr. 28 (3), 433–460.2.0.CO;2>CrossRefGoogle Scholar
Chen, C. & Kamenkovich, I. 2013 Effects of topography on baroclinic instability. J. Phys. Oceanogr. 43 (4), 790–804.CrossRefGoogle Scholar
Chen, C., Kamenkovich, I. & Berloff, P. 2015 On the dynamics of flows induced by topographic ridges. J. Phys. Oceanogr. 45 (3), 927–940.CrossRefGoogle Scholar
Gille, S.T., Metzger, E.J. & Tokmakian, R. 2004 Seafloor topography and ocean circulation. Oceanography 17 (1), 47–54.CrossRefGoogle Scholar
Hart, J.E. 1975 a Baroclinic instability over a slope. Part 1. Linear theory. J. Phys. Oceanogr. 5 (4), 625–633.2.0.CO;2>CrossRefGoogle Scholar
Hart, J.E. 1975 b Baroclinic instability over a slope. Part 2. Finite-amplitude theory. J. Phys. Oceanogr. 5 (4), 634–641.2.0.CO;2>CrossRefGoogle Scholar
Khatri, H. & Berloff, P. 2018 A mechanism for jet drift over topography. J. Fluid Mech. 845, 392–416.CrossRefGoogle Scholar
Khatri, H. & Berloff, P. 2019 Tilted drifting jets over a zonally sloped topography: effects of vanishing eddy viscosity. J. Fluid Mech. 876, 939–961.CrossRefGoogle Scholar
Killworth, P.D. 1980 Barotropic and baroclinic instability in rotating stratified fluids. Dyn. Atmos. Oceans 4 (3), 143–184.CrossRefGoogle Scholar
Klocker, A. 2018 Opening the window to the southern ocean: the role of jet dynamics. Sci. Adv. 4 (10), eaao4719.CrossRefGoogle ScholarPubMed
LaCasce, J.H., Escartin, J., Chassignet, E.P. & Xu, X. 2019 Jet instability over smooth, corrugated, and realistic bathymetry. J. Phys. Oceanogr. 49 (2), 585–605.CrossRefGoogle Scholar
Lazar, A., Zhang, Q. & Thompson, A.F. 2018 Submesoscale turbulence over a topographic slope. Fluids 3 (2), 32.CrossRefGoogle Scholar
Lorenz, E.N. 1972 Barotropic instability of Rossby wave motion. J. Atmos. Sci. 29 (2), 258–265.2.0.CO;2>CrossRefGoogle Scholar
Marshall, D. 1995 Influence of topography on the large-scale ocean circulation. J. Phys. Oceanogr. 25 (7), 1622–1635.2.0.CO;2>CrossRefGoogle Scholar
Niino, H. & Misawa, N. 1984 An experimental and theoretical study of barotropic instability. J. Atmos. Sci. 41 (12), 1992–2011.2.0.CO;2>CrossRefGoogle Scholar
Orlanski, I. & Cox, M.D. 1972 Baroclinic instability in ocean currents. Geophys. Astrophys. Fluid Dyn. 4 (1), 297–332.CrossRefGoogle Scholar
Patmore, R.D., Holland, P.R., Munday, D.R., Naveira Garabato, A.C., Stevens, D.P. & Meredith, M.P. 2019 Topographic control of southern ocean gyres and the Antarctic circumpolar current: a barotropic perspective. J. Phys. Oceanogr. 49 (12), 3221–3244.CrossRefGoogle Scholar
Pedlosky, J. 1964 The stability of currents in the atmosphere and the ocean: Part I. J. Atmosp. Sci. 21 (2), 201–219.2.0.CO;2>CrossRefGoogle Scholar
Radko, T. 2020 Control of baroclinic instability by submesoscale topography. J. Fluid Mech. 882.CrossRefGoogle Scholar
Rhines, P.B. 1977 The dynamics of unsteady currents. In The Sea (ed. E.D. Goldberg, I.N. McCave, J.J. O'Brien & J.H. Steele), vol. 6, pp. 189–318. Wiley-Interscience.Google Scholar
Shevchenko, I.V., Berloff, P.S., Guerrero-López, D. & Roman, J.E. 2016 On low-frequency variability of the midlatitude ocean gyres. J. Fluid Mech. 795, 423–442.CrossRefGoogle Scholar
Smith, K.S. 2007 Eddy amplitudes in baroclinic turbulence driven by nonzonal mean flow: shear dispersion of potential vorticity. J. Phys. Oceanogr. 37 (4), 1037–1050.CrossRefGoogle Scholar
Stern, A., Nadeau, L.-P. & Holland, D. 2015 Instability and mixing of zonal jets along an idealized continental shelf break. J. Phys. Oceanogr. 45 (9), 2315–2338.CrossRefGoogle Scholar
Sutyrin, G. 2007 Ageostrophic instabilities in a baroclinic flow over sloping topography. In Congrès français de mécanique. AFM, Maison de la Mécanique, 39/41 rue Louis Blanc-92400 Courbevoie.Google Scholar
Tamsitt, V., et al. . 2017 Spiraling pathways of global deep waters to the surface of the southern ocean. Nat. Commun. 8 (1), 1–10.CrossRefGoogle ScholarPubMed
Tang, C.-M. 1975 Baroclinic instability of stratified shear flows in the ocean and atmosphere. J. Geophys. Res. 80 (9), 1168–1175.CrossRefGoogle Scholar
Thompson, A.F. 2010 Jet formation and evolution in baroclinic turbulence with simple topography. J. Phys. Oceanogr. 40 (2), 257–278.CrossRefGoogle Scholar
Thompson, A.F. & Naveira Garabato, A.C. 2014 Equilibration of the Antarctic circumpolar current by standing meanders. J. Phys. Oceanogr. 44 (7), 1811–1828.CrossRefGoogle Scholar
Thompson, A.F. & Richards, K.J. 2011 Low frequency variability of southern ocean jets. J. Geophys. Res. 116, C9.CrossRefGoogle Scholar
Thompson, A.F. & Sallée, J. -B. 2012 Jets and topography: jet transitions and the impact on transport in the Antarctic circumpolar current. J. Phys. Oceanogr. 42 (6), 956–972.CrossRefGoogle Scholar
Vallis, G.K. 2017 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Vanneste, J. 2003 Nonlinear dynamics over rough topography: homogeneous and stratified quasi-geostrophic theory. J. Fluid Mech. 474, 299–318.CrossRefGoogle Scholar
Waterman, S. & Hoskins, B.J. 2013 Eddy shape, orientation, propagation, and mean flow feedback in western boundary current jets. J. Phys. Oceanogr. 43 (8), 1666–1690.CrossRefGoogle Scholar
Williams, P.D., Read, P.L. & Haine, T.W.N. 2010 Testing the limits of quasi-geostrophic theory: application to observed laboratory flows outside the quasi-geostrophic regime. J. Fluid. Mech. 649, 187–203.CrossRefGoogle Scholar
Youngs, M.K., Thompson, A.F., Lazar, A. & Richards, K.J. 2017 Acc meanders, energy transfer, and mixed barotropic–baroclinic instability. J. Phys. Oceanogr. 47 (6), 1291–1305.CrossRefGoogle Scholar