Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-02T22:20:41.948Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants of the reduced velocity gradient tensor in turbulent flows

Published online by Cambridge University Press:  28 January 2013

J. I. Cardesa ,
D. Mistry ,
L. Gan  and
J. R. Dawson
J. I. Cardesa*
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
D. Mistry
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
L. Gan
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
J. R. Dawson
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

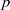In this paper we examine the invariants $p$ and 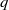$q$ of the reduced 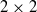$2\times 2$ velocity gradient tensor (VGT) formed from a two-dimensional (2D) slice of an incompressible three-dimensional (3D) flow. Using data from both 2D particle image velocimetry (PIV) measurements and 3D direct numerical simulations of various turbulent flows, we show that the joint probability density functions (p.d.f.s) of 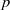$p$ and 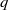$q$ exhibit a common characteristic asymmetric shape consistent with 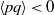$\langle pq\rangle \lt 0$. An explanation for this inequality is proposed. Assuming local homogeneity we derive 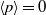$\langle p\rangle = 0$ and 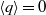$\langle q\rangle = 0$. With the addition of local isotropy the sign of 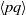$\langle pq\rangle $ is proved to be the same as that of the skewness of 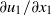$\partial {u}_{1} / \partial {x}_{1} $, hence negative. This suggests that the observed asymmetry in the joint p.d.f.s of 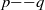$p{{\ndash}}q$ stems from the universal predominance of vortex stretching at the smallest scales. Some advantages of this joint p.d.f. compared with that of 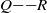$Q{{\ndash}}R$ obtained from the full 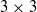$3\times 3$ VGT are discussed. Analysing the eigenvalues of the reduced strain-rate matrix associated with the reduced VGT, we prove that in some cases the 2D data can unambiguously discriminate between the bi-axial (sheet-forming) and axial (tube-forming) strain-rate configurations of the full 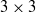$3\times 3$ strain-rate tensor.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 597 - 615
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Almalkie, S. & de Bruyn Kops, S. M. 2012 Energy dissipation rate surrogates in incompressible Navier–Stokes turbulence. J. Fluid Mech. 697, 204–236.Google Scholar
Atkinson, C., Coudert, S., Foucaut, J.-M., Stanislas, M. & Soria, J. 2011 The accuracy of tomographic particle image velocimetry for measurements of a turbulent boundary layer. Exp. Fluids 50, 1031–1056.Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1 (5), 497–504.Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2010 Amplification of enstrophy in the far field of an axisymmetric turbulent jet. J. Fluid Mech. 651, 483–502.CrossRefGoogle Scholar
Buxton, O., Laizet, S. & Ganapathisubramani, B. 2011 The effects of resolution and noise on kinematic features of fine-scale turbulence. Exp. Fluids 51, 1417–1437.Google Scholar
Champagne, F. H. 1978 The fine-scale structure of the turbulent velocity field. J. Fluid Mech. 86, 67–108.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.CrossRefGoogle Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.Google Scholar
Gulitski, G., Kholmyansky, M., Kinzelbach, W., Lüthi, B., Tsinober, A. & Yorish, S. 2007 Velocity and temperature derivatives in high-Reynolds-number turbulent flows in the atmospheric surface layer. Part 1. Facilities, methods and some general results. J. Fluid Mech. 589, 57–81.Google Scholar
Hearst, R., Buxton, O., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 1–18.Google Scholar
Hierro, J. & Dopazo, C. 2003 Fourth-order statistical moments of the velocity gradient tensor in homogeneous, isotropic turbulence. Phys. Fluids 15 (11), 3434–3442.CrossRefGoogle Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. N31.CrossRefGoogle Scholar
Lüthi, B., Holzner, M. & Tsinober, A. 2009 Expanding the $Q$ – $R$ space to three dimensions. J. Fluid Mech. 641, 497–507.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.Google Scholar
Ooi, A, Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Perlman, E., Burns, R., Li, Y. & Meneveau, C. 2007 Data exploration of turbulence simulations using a database cluster. In Proceedings of the 2007 ACM/IEEE Conference on Supercomputing, SC ’07, pp. 23:1–23:11. ACM.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125–155.Google Scholar
Perry, A. E. & Chong, M. S. 1994 Topology of flow patterns in vortex motions and turbulence. Appl. Sci. Res. 53, 357–374.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Siggia, E. D. 1981 Invariants for the one-point vorticity and strain rate correlation functions. Phys. Fluids 24 (11), 1934–1936.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6 (2), 871–884.Google Scholar
Tavoularis, S., Bennett, J. C. & Corrsin, S. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88 (1), 63–69.Google Scholar
Townsend, A. A. 1951 On the fine-scale structure of turbulence. Proc. R. Soc. Lond. Ser. A. Mathematical and Physical Sciences 208, 534–542.Google Scholar
Wallace, J. M. & Vukoslavčević, P. V. 2010 Measurement of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 42, 157–181.Google Scholar
Worth, N. A. 2010 Tomographic-PIV measurement of coherent dissipation scale structures. PhD thesis, Cambridge. http://www.dspace.cam.ac.uk/handle/1810/237242.Google Scholar
Worth, N. A. & Nickels, T. B. 2011 Some characteristics of thin shear layers in homogeneous turbulent flow. Phil. Trans. R. Soc. Lond. 369, 709–722.Google Scholar
Worth, N., Nickels, T. & Swaminathan, N. 2010 A tomographic PIV resolution study based on homogeneous isotropic turbulence DNS data. Exp. Fluids 49, 637–656.CrossRefGoogle Scholar