Published online by Cambridge University Press: 06 October 2021
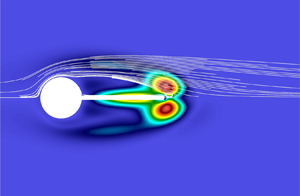
This paper investigates the origin of flow-induced instabilities and their sensitivities in a flow over a rotationally flexible circular cylinder with a rigid splitter plate. A linear stability and sensitivity problem is formulated in the Eulerian frame by considering the geometric nonlinearity arising from the rotational motion of the cylinder which is not present in the stationary or purely translating stability methodology. This nonlinearity needs careful and consistent treatment in the linearised problem particularly when considering the Eulerian frame or reference adopted in this study that is not so widely considered. Two types of instabilities arising from the fluid–structure interaction are found. The first type of instabilities is the stationary symmetry breaking mode, which was well reported in previous studies. This instability exhibits a strong correlation with the length of the recirculation zone. A detailed analysis of the instability mode and its sensitivity reveals the importance of the flow near the tip region of the plate for the generation and control of this instability mode. The second type is an oscillatory torsional flapping mode, which has not been well reported. This instability typically emerges when the length of the splitter plate is sufficiently long. Unlike the symmetry breaking mode, it is not so closely correlated with the length of the recirculation zone. The sensitivity analysis however also reveals the crucial role played by the flow near the tip region in this instability. Finally, it is found that many physical features of this instability are reminiscent of those of the flapping (or flutter instability) observed in a flow over a flexible plate or a flag, suggesting that these instabilities share the same physical origin.