Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T01:17:16.836Z Has data issue: false hasContentIssue false
  • English
  • Français

Impinging planar jets: hysteretic behaviour and origin of the self-sustained oscillations

Published online by Cambridge University Press:  03 March 2021

Alessandro Bongarzone Open the ORCID record for Alessandro Bongarzone [Opens in a new window] ,
Arnaud Bertsch Open the ORCID record for Arnaud Bertsch [Opens in a new window] ,
Philippe Renaud Open the ORCID record for Philippe Renaud [Opens in a new window]  and
François Gallaire Open the ORCID record for François Gallaire [Opens in a new window]
Alessandro Bongarzone
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, LausanneCH-1015, Switzerland
Arnaud Bertsch
Affiliation:
Microsystems Laboratory LMIS4, École Polytechnique Fédérale de Lausanne, LausanneCH-1015, Switzerland
Philippe Renaud
Affiliation:
Microsystems Laboratory LMIS4, École Polytechnique Fédérale de Lausanne, LausanneCH-1015, Switzerland
François Gallaire*
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, LausanneCH-1015, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

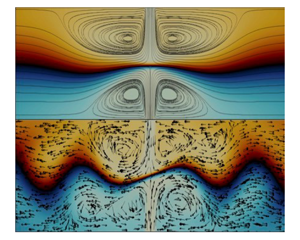
The experimental and numerical investigation presented by Bertsch et al. (Phys. Rev. Fluids, vol. 5, 2020a, p. 054202) describes the self-sustained oscillations induced by the interaction of two impinging jets in microfluidic devices. While the oscillatory regime induced by interacting jets has been studied in detail, the physical mechanism behind these oscillations remains still undetermined. The present paper focuses on two-dimensional oscillators subjected to a fully developed inlet flow, as in Bertsch et al. (Phys. Rev. Fluids, vol. 5, 2020a, p. 054202) and in contradistinction with Pawlowski et al. (J. Fluid Mech., vol. 551, 2006, pp. 117–139), who focused on plug inlet flow. The linear global stability analysis performed confirms the existence of an oscillating global mode, whose spatial structure qualitatively coincides with that computed numerically by Bertsch et al. (Phys. Rev. Fluids, vol. 5, 2020a, p. 054202), suggesting that the physical mechanism from which the oscillations would originate is predominantly two-dimensional. The interaction of the oscillating mode with a steady symmetry-breaking mode is examined making use of the weakly nonlinear theory, which shows how the system exhibits hysteresis in a certain range of aspect ratios. Lastly, sensitivity analysis is exploited to identify the wavemaker associated with the global modes, whose examination allows us to spot the core of the symmetry-breaking instability at the stagnation point and to identify the Kelvin–Helmholtz instability, located in the jets interaction region, as the main candidate for the origin of the oscillations observed in fluidic devices.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Nonlinear Dynamical Systems: Bifurcation Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A51
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Barkley, D., Gomes, M.G.M. & Henderson, R.D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
Bertsch, A., Bongarzone, A., Duchamp, M., Renaud, P. & Gallaire, F. 2020 a Feedback-free microfluidic oscillator with impinging jets. Phys. Rev. Fluids 5 (5), 054202.CrossRefGoogle Scholar
Bertsch, A., Bongarzone, A., Yim, E., Renaud, P. & Gallaire, F. 2020 b Swinging jets. Phys. Rev. Fluids 5 (11), 110505.CrossRefGoogle Scholar
Biancofiore, L. & Gallaire, F. 2011 The influence of shear layer thickness on the stability of confined two-dimensional wakes. Phys. Fluids 23 (3), 034103.CrossRefGoogle Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.CrossRefGoogle Scholar
Burshtein, N., Shen, A.Q. & Haward, S.J. 2019 Controlled symmetry breaking and vortex dynamics in intersecting flows. Phys. Fluids 31 (3), 034104.CrossRefGoogle Scholar
Camarri, S. & Iollo, A. 2010 Feedback control of the vortex-shedding instability based on sensitivity analysis. Phys. Fluids 22 (9), 094102.CrossRefGoogle Scholar
Camarri, S. & Mengali, G. 2019 Stability properties of the mean flow after a steady symmetry-breaking bifurcation and prediction of the nonlinear saturation. Acta Mechanica 230 (9), 3127–3141.CrossRefGoogle Scholar
Chomaz, J.M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Chomaz, J.M., Huerre, P. & Redekopp, L.G. 1988 Bifurcations to local and global modes in spatially developing flows. Phys. Rev. Lett. 60 (1), 25–28.CrossRefGoogle ScholarPubMed
Crawford, J.D. & Knobloch, E. 1991 Symmetry and symmetry-breaking bifurcations in fluid dynamics. Annu. Rev. Fluid Mech. 23 (1), 341–387.CrossRefGoogle Scholar
Davis, T.A. & Duff, I.S. 1997 An unsymmetric-pattern multifrontal method for sparse LU factorization. SIAM J. Matrix Anal. Appl. 18 (1), 140–158.CrossRefGoogle Scholar
Denshchikov, V.A., Kondrat'ev, V.N. & Romashov, A.N. 1978 Interaction between two opposed jets. Fluid Dyn. 13 (6), 924–926.CrossRefGoogle Scholar
Denshchikov, V.A., Kondrat'ev, V.N., Romashov, A.N. & Chubarov, V.M. 1983 Auto-oscillations of planar colliding jets. Fluid Dyn. 18 (3), 460–462.CrossRefGoogle Scholar
Ding, Y. & Kawahara, M. 1999 Three-dimensional linear stability analysis of incompressible viscous flows using the finite element method. Intl J. Numer. Meth. Fluids 31 (2), 451–479.3.0.CO;2-O>CrossRefGoogle Scholar
Fani, A., Camarri, S. & Salvetti, M.V. 2012 Stability analysis and control of the flow in a symmetric channel with a sudden expansion. Phys. Fluids 24 (8), 084102.CrossRefGoogle Scholar
Friedlander, S. & Vishik, M.M. 1991 Instability criteria for the flow of an inviscid incompressible fluid. Phys. Rev. Lett. 66 (17), 2204–2206.CrossRefGoogle ScholarPubMed
Friedrichs, K.O. 2012 Spectral Theory of Operators in Hilbert Space. Springer Science & Business Media.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P.J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.CrossRefGoogle Scholar
Giannetti, F., Camarri, S. & Citro, V. 2019 Sensitivity analysis and passive control of the secondary instability in the wake of a cylinder. J. Fluid Mech. 864, 45–72.CrossRefGoogle Scholar
Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Godeferd, F.S., Cambon, C. & Leblanc, S. 2001 Zonal approach to centrifugal, elliptic and hyperbolic instabilities in stuart vortices with external rotation. J. Fluid Mech. 449, 1–37.CrossRefGoogle Scholar
Healey, J.J. 2009 Destabilizing effects of confinement on homogeneous mixing layers. J. Fluid Mech. 623, 241–271.CrossRefGoogle Scholar
Hecht, F., Pironneau, O., Hyaric, A.L. & Ohtsuka, K. 2011 Freefem++ Manual, 3rd edn. Available at: http://www.freefem.org/ff++/.Google Scholar
Huerre, P. & Monkewitz, P.A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Juniper, M.P. 2006 The effect of confinement on the stability of two-dimensional shear flows. J. Fluid Mech. 565, 171–195.CrossRefGoogle Scholar
Karniadakis, G.E., Israeli, M. & Orszag, S.A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Kuznetsov, Y.A. 2013 Elements of Applied Bifurcation Theory. Springer Science & Business Media.Google Scholar
Lanzerstorfer, D. & Kuhlmann, H.G. 2012 Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.CrossRefGoogle Scholar
Lashgari, I., Tammisola, O., Citro, V., Juniper, M.P. & Brandt, L. 2014 The planar X-junction flow: stability analysis and control. J. Fluid Mech. 753, 1–28.CrossRefGoogle Scholar
Ledda, P.G., Siconolfi, L., Viola, F., Gallaire, F. & Camarri, S. 2018 Suppression of von Kármán vortex streets past porous rectangular cylinders. Phys. Rev. Fluids 3 (10), 103901.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A: Fluid Dyn. 3 (11), 2644–2651.CrossRefGoogle Scholar
Liu, S., Wang, B., Wan, Z., Ma, D. & Sun, D. 2016 Bifurcation analysis of laminar isothermal planar opposed-jet flow. Comput. Fluids 140, 72–80.CrossRefGoogle Scholar
Lottes, J.W., Fischer, P.F. & Kerkemeier, S.G. 2008 Nek5000 Webpage. Available at: http://nek5000.mcs.anl.gov.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Meliga, P., Chomaz, J.M. & Sipp, D. 2009 a Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.CrossRefGoogle Scholar
Meliga, P., Chomaz, J.M. & Sipp, D. 2009 b Unsteadiness in the wake of disks and spheres: instability, receptivity and control using direct and adjoint global stability analyses. J. Fluids Struct. 25 (4), 601–616.CrossRefGoogle Scholar
Meliga, P. & Gallaire, F. 2011 Control of axisymmetric vortex breakdown in a constricted pipe: nonlinear steady states and weakly nonlinear asymptotic expansions. Phys. Fluids 23 (8), 084102.CrossRefGoogle Scholar
Meliga, P., Gallaire, F. & Chomaz, J.M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.CrossRefGoogle Scholar
Ortiz, S. & Chomaz, J.M. 2011 Transient growth of secondary instabilities in parallel wakes: anti lift-up mechanism and hyperbolic instability. Phys. Fluids 23 (11), 114106.CrossRefGoogle Scholar
Pawlowski, R.P., Salinger, A.G., Shadid, J.N. & Mountziaris, T.J. 2006 Bifurcation and stability analysis of laminar isothermal counterflowing jets. J. Fluid Mech. 551, 117–139.CrossRefGoogle Scholar
Rees, S.J. & Juniper, M.P. 2010 The effect of confinement on the stability of viscous planar jets and wakes. J. Fluid Mech. 656, 309–336.CrossRefGoogle Scholar
Siconolfi, L., Citro, V., Giannetti, F., Camarri, S. & Luchini, P. 2017 Towards a quantitative comparison between global and local stability analysis. J. Fluid Mech. 819, 147–164.CrossRefGoogle Scholar
Sipp, D., Lauga, E. & Jacquin, L. 1999 Vortices in rotating systems: centrifugal, elliptic and hyperbolic type instabilities. Phys. Fluids 11 (12), 3716–3728.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
Tesař, V. 2009 Oscillator micromixer. Chem. Engng J. 155 (3), 789–799.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Villermaux, E., Gagne, Y. & Hopfinger, E.J. 1993 Self sustained oscillations and collective behaviours in a lattice of jets. Appl. Sci. Res. 51 (1-2), 243–248.CrossRefGoogle Scholar
Villermaux, E. & Hopfinger, E.J. 1994 Self-sustained oscillations of a confined jet: a case study for the non-linear delayed saturation model. Physica D 72 (3), 230–243.CrossRefGoogle Scholar
Viola, F., Arratia, C. & Gallaire, F. 2016 Mode selection in trailing vortices: harmonic response of the non-parallel Batchelor vortex. J. Fluid Mech. 790, 523–552.CrossRefGoogle Scholar
Zhu, L. & Gallaire, F. 2017 Bifurcation dynamics of a particle-encapsulating droplet in shear flow. Phys. Rev. Lett. 119 (6), 064502.CrossRefGoogle ScholarPubMed